不可逆空气热泵循环供热率密度优化

毕月虹,陈林根,孙丰瑞

(1.北京工业大学建工学院,北京 100124;2.海军工程大学研究生院,湖北 武汉 430033)

0 引 言

近年来,环保的迫切要求使得对空气热泵循环的研究再次活跃起来,并开始用有限时间热力学理论来研究[1～4]。已有一些文献研究了恒温和变温热源条件下内可逆简单循环、不可逆简单循环、内可逆回热循环和不可逆回热循环[5～9]的性能,导出了供热率和供热系数解析关系[10]。研究不同优化目标下热力循环的基本优化特性和各种热力学参数的优选范围,已成为近年来有限时间热力学领域一项十分活跃的研究工作[10～18]。对于空气热泵循环,可在高、低温换热器的总热导率一定的条件下优化换热器的热导率分配,来获得循环的最优性能,针对变温热源条件,还可对工质与热源间的热容率匹配作优化[19]。文献[20～25]均对内可逆空气热泵循环在不同性能指标下的最优化问题进行了研究,其中,文献[20]进行了恒温热源条件下的内可逆空气热泵的供热率和供热系数以及供热率密度 (即供热率与循环中工质最大比容之比)优化,研究了高、低温侧换热器的热导率最优分配,文献[21]则深入分析了供热率密度优化对有效减小内可逆空气热泵尺寸的影响,本文除考虑热阻损失外,同时还考虑空气压缩机和涡轮膨胀机中的不可逆压缩和膨胀损失,研究恒温热源不可逆空气热泵循环的供热率密度优化,得到同时兼顾空气热泵的供热率及其尺寸的新的性能特性。

1 不可逆空气热泵循环模型

图1为不可逆恒温热源空气热泵循环1-2-3-4-1,其中1-2为从低温热源吸热过程,2-3为压缩机中的不可逆压缩过程,3-4为向高温热源放热过程,4-1为膨胀机中不可逆膨胀过程,2-3 s和4-1 s为与2-3和4-1相对应的等熵压缩和膨胀过程。设高、低温侧换热器的热导率 (传热系数K与传热面积F乘积)分别为UH,UL;高、低温热源温度分别为 TH,TL;工质为理想气体,有恒热容率 (质量流率与定压比热之积)Cwf。

图1 恒温热源不可逆空气热泵循环模型Fig.1 Model of an irreversible air heat pump cycle with constant-temperature heat reservoirs

2 解析关系

2.1 供热率与供热系数

由热源与工质间的传热和换热器理论可有循环放热流率 (供热率)QH和吸热流率QL分别为

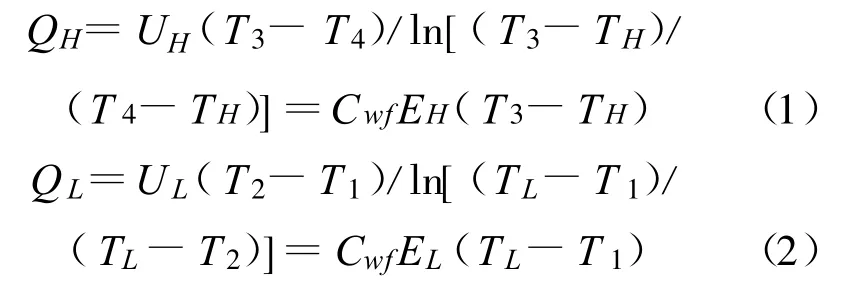
式中:EH,EL分别为高、低温侧换热器的有效度,即有:

式中:NH和NL为高、低温侧换热器的传热单元数,即有:

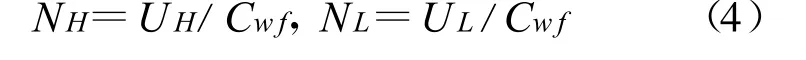
循环的内不可逆性用压缩机和膨胀机效率ηc、ηt来表征[6]:

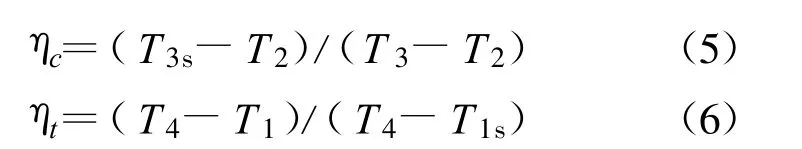
对内可逆循环有 T2T4=T1sT3s,定义压缩机内的工质等熵温比为

式中:m=(k-1)/k,k为工质的绝热指数,π为压缩机的压比,P为压力。

由以上模型,文献[10]已经导出循环的供热率Qμ和供热系数β分别为

式中:τ1=TH/TL,为高、低温热源温比。定义无因次供热率=QH/(CwfTH)

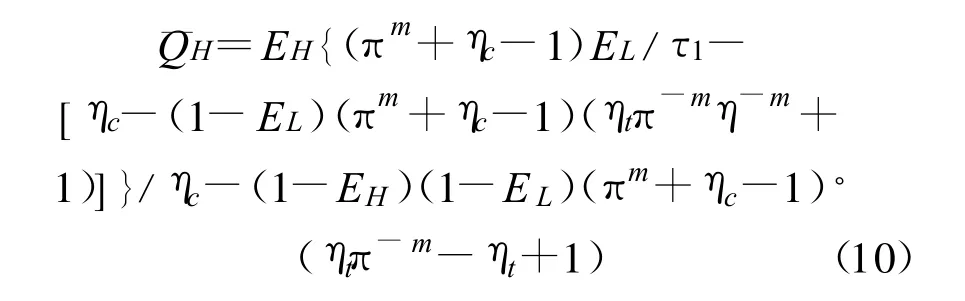
2.2 供热率密度

根据供热率密度的定义[26](即供热率与循环中工质最大比容之比),在图1所示循环中,2点为工质比容最大点,循环的供热率密度:qH=QH/v2。为便于分析,供热率密度写成无因次的形式:

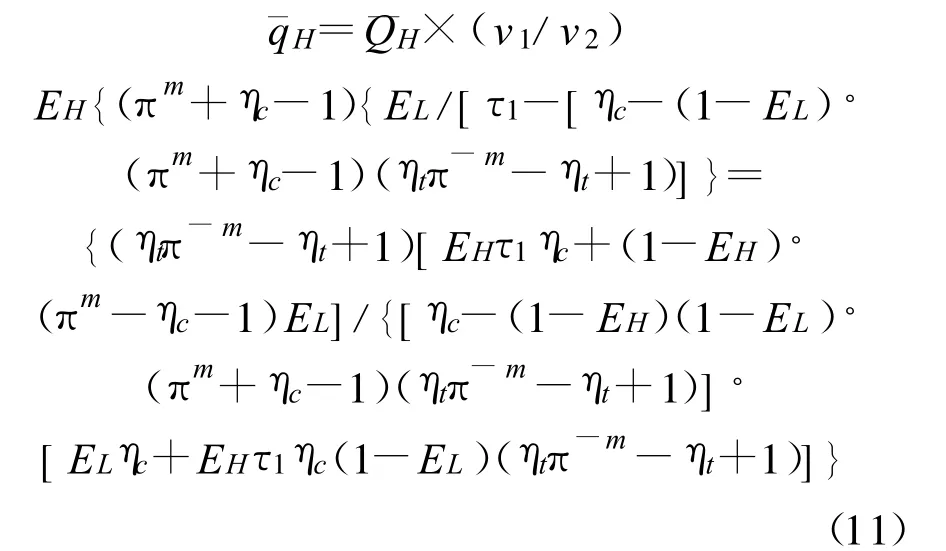
3 最优性能

3.1 各参数对供热率密度的影响

图2给出了 k=1.4,EH=EL=0.9,ηc=ηt=0.8时热源温比 τ1对无因次供热率密度与压比π关系的影响,由图可知,供热率密度与压比呈单调递增关系,图2还表明,无因次供热率密度随着热源温比 τ1的增大而减小,并且无因次供热率密度为零的压比值随热源温比 τ1的提高而增加。

图2 热源温比τ1对- π关系的影响Fig.2 Effect of heat reservoir temperature ratio on the dimensionless heaing load density vs.pressure ratio

图3给出了 k=1.4,EH=EL=0.9,τ1=1.25时不同的压缩机和膨胀机效率 ηc、ηt下无因次供热率密度与压比π的关系。由图可知,无因次供热率密度随着和的增大而降低。

图3 压缩机和膨胀机效率 ηc、 ηt对- π关系的影响Fig.3 Effect of efficiencies of the compressor and expander on the dimensionless heating load density vs.pressure ratio

图4给出了 k=1.4,τ1=1.25,ηc=ηt=0.8时高、低温侧换热器的有效度 EH,EL对无因次供热率密度与压比π关系的影响。由图可知,无因次供热率密度与高、低温侧换热器的有效度呈单调递增关系。

图4 换热器有效度 EH、EL对 π关系的影响Fig.4 Effect of effectivenesses of the heat exchangers on the dimensionless heating load density vs.pressure ratio

3.2 热导率最优分配及最优性能

在高、低温侧换热器总热导率一定的条件下优化其分配,也即在约束条件 UH+UL=UT下,求 u=UL/UT的最佳值,使得循环的供热率密度取得最大值。因此有UL+uUT,UH=(1-u)UT。图5给出了 k=1.4,τ1=1.25,Cwf=0.8 kW/K,UT=5 kW/K,ηc=ηt=0.8 时不同压比π下的无因次供热率密度与热导率分配u间的关系,由图可知,无因次供热率密度与热导率分配呈类抛物线关系,这说明,每一确定的压比都对应一个最佳热导率分配值,使得无因次供热率密度取得最大值max,u,当压比变化时,便可得到最佳热导率分配值与压比的关系。

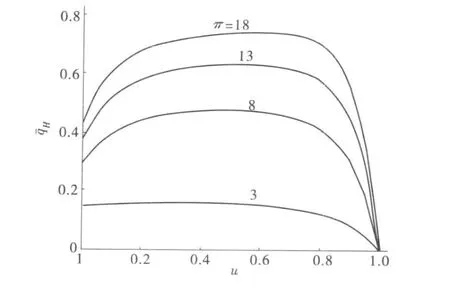
图5 压比 π对-u关系的影响Fig.5 Effect of pressure ratio on the dimensionless heating load density vs.distribution of heat conductance

3.2.1 热源温比的影响

图6给出了k=1.4,Cwf=0.8 kW/K,UT=5 kW/K,ηc=ηt=0.8时不同热源温比 τ1下的最佳热导率分配值与压比π间的关系,该图说明,当温比增加时,最佳热导率分配值下降,而且当压比较小时,最佳热导率分配值随着压比的增大递增明显,当压比超过一定值后,递增速度减缓。

图6 热源温比 τ1对 -π关系的影响Fig.6 Effect of heat reservoir temperature ratio on the optimum distribution of heat conductance vs.pressure ratio

图7给出了 K=1.4,Cwf=0.8 kW/K,UT=5 kW/K, ηc=ηt=0.8 时不同 τ1下的最大无因次供热率密度与压比 π的关系,该图说明,最大无因次供热率密度随着热源温比的增大而减小。

图7 热源温比τ1对-π关系的影响Fig.7 Effect of heat reservoir temperature ratio on the maximum dimensionless heating load density vs.pressure ratio

3.2.2 总热导率的影响

图8给出了 k=1.4,Cwf=0.8kW/K,τ1=1.25,ηc=ηt=0.8时不同总热导率 UT下的最佳热导率分配值uopt,与压比π间的关系,该图说明,当压比较小时,uopt,¯qn随总热导率增大而增大,而且当 UT提高到一定值后再继续提高UT,递增量越来越小,当压比超过一定值后,u转变为随总热导率的增大而无规律变化,压比再进一步增大,则又变为随总热导率增大而增大。

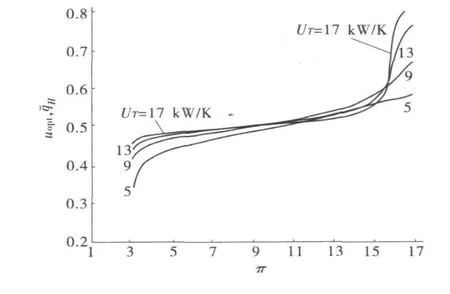
图8 总热导率 UT对uopt,-π关系的影响Fig.8 Effect of heat exchanger inventory on the optimum distribution of heat conductance vs.pressure ratio

图9给出了 k=1.4,τ1=1.25,Cwf=0.8 kW/K,ηc=ηt=0.8时总热导率 UT对最大无因次供热率密度与压比π关系的影响。由图可知,最大无因次供热率密度随着总热导率的增大而增大,而且当 UT提高到一定值后再继续提高UT,递增量越来越小。

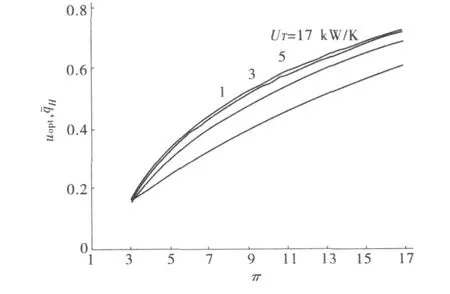
图9 总热导率 UT对¯qHmax,u-π关系的影响Fig.9 Effect of heat exchanger inventory on the maximum dimensionless heating load density vs.pressure ratio

3.2.3 压缩机和膨胀机效率的影响

图10给出 k=1.4,τ1=1.25,Cwf=0.8 kW/K,UT=5 kW/K时压缩机和膨胀机效率 、对最佳热导率分配 u与压比π关系的影响。图中 ηc=ηt=1为内可逆循环,此时,≥0.5,由图可知,对于 ηc＜1和 ηt＜1的不可逆循环,当压比较小时,u随着压缩机和膨胀机效率的增大而增大,当压比超过一定值后,u转变为随着压缩机和膨胀机效率的增大而减小。

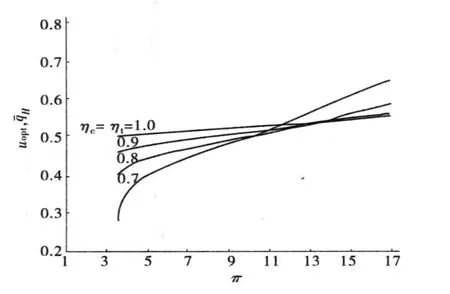
图10 压缩机和膨胀机效率 ηc、ηt对uopt,-π 关系的影响Fig.10 Effect of efficiencies of the compressor and expander on the optimum distribution of heat conductance vs.pressure ratio

图11给出了 k=1.4,τ1=1.25,Cwf=0.8 kW/K,UT=5 kW/K时压缩机和膨胀机效率ηc、ηt对最大无因次供热率密度与压比 π关系的影响。图中,ηc=ηt=1为内可逆循环,由图可知,最大无因次供热率密度随着压缩机和膨胀机效率的增大而减小。

图11 压缩机和膨胀机效率 ηc、ηt对-π关系的影响Fig.11 Effect of efficiencies of the compressor on the maximum dimensionless heating load density vs.pressure ratio

4 结 论

本文对恒温热源不可逆空气热泵循环以供热率密度为热力学优化目标作了优化,得出了供热率密度与压比及换热器有效度等参数间的关系,讨论了热源温比、换热器总热导率、压缩机和膨胀机效率等参数对热导率最优分配及最优性能的影响。研究结果对实际空气热泵的设计具有一定的指导意义。

[1]Heikkinen M A,Lampinen M J,Tamasy-Bano M.Thermodynamic analysis and optimization of the Brayton process in a heat recovery system of paper machines[J].Heat Recovery Systems and CHP,1993,13(2):123-131.

[2]Angelino G,Invernizzi C.Prospects for real-gas reversed Brayton cycle heat pumps[J].Int.J.Refrig.,1995,18(4):272-280.

[3]Fleming J S,Van der Wekken B J C,Mcgovern J A,Van Gerwen R J M.Air cycle cooling and heating,Part 1:A realistic appraisal and a chosen application[J].Int.J.Energy Res.,1998,22(7):639-655.

[4]Fleming J S,Li L,Van der Wekken B J C.Air cycle cooling and heating,Part 2:A mathematical model for the transient behaviour of fixed matrix regenerators[J].Int.J.Energy Res.,1998,22(5):463-476.

[5]Wu C,Chen L,Sun F.Optimization of steady flow heat pumps[J].EnergyConversion and Management,1998,39(5/6):445-453.

[6]Chen L,Ni N,Wu C,Sun F.Heating load vs.COP characteristics for irreversible air-heat pump cycles[J].Int.J.Pow.Energy Systems,2001,21(2):105-111.

[7]Ni N,Chen L,Wu C,Sun F.Performance analysis for endoreversible closed regenerated Brayton heat pump cycles[J].Energy Conversion and Management,1999,40(4):393-406.

[8]Chen L,Ni N,Sun F,Wu C.Performance of real regenerated air heat pumps[J].Int.J.Power and Energy Systems,1999,19(3):231-238.

[9]Chen L,Ni N,Wu C,Sun F.Performance analysis of a closed regenerated Brayton heat pump with internal irreversibilities[J].Int.J.of Energy Research,1999,23(12):1039-1050.

[10]陈林根.不可逆过程和循环的有限时间热力学分析[M].北京:高等教育出版社,2005.Chen L.Finite Time Thermodynamic Analysis of Irreversible Processes and Cycles[M].Higher Education Press,Beijing,2005.

[11]Bejan A.Entropy Generation Minimization[M].New York:Wi1ey,1996.

[12]Berry R S,Kazakov V,Sieniutycz S,Szwast Z and Tsirlin A M.Thermodynamic Optimization of Finite-Time Processes[M].New York:John Wiley&Sons,LTD,1999.

[13]Bejan A,Lorente S.Constructal multi-scale and multi-objective structures[J].Int.J.Energy Res.,2005,29(7):689-710.

[14]Chen L,Bi Y,Sun F,et al.Performance optimization of a combined heat pump cycle[J].Open System&Information Dynamics,2003,10(4):377-389.

[15]Wu S,Lin G,Chen J.Optimum thermoeconomic and thermodynamic performance characteristics of an irreversible three-heat-source heat pump[J].Renewable Energy,2005,30(15):2257-2271.

[16]Morosuk T,Nikulshin R,Morosuk L.Entropy-cycle method for analysis of refrigeration machine and heat pump cycles[J].Thermal Science,2006,10(1):111-124.

[17]Ozgener O,Hepbasli A.A review on the energy and exergy analysis of solar assisted heat pump systems[J].Renewable and Sustainable EnergyReviews,2007,11(3):482-496.

[18]Sarkar J,Bhattacharyya S.Overall conductance and heat transfer area minimization of refrigerators and heat pumps with finite heat reservoirs[J].Energy Conversion and Management,2007,48(3):803-808.

[19]毕月虹.空气热泵性能有限时间热力学优化[D].博士后研究工作报告,海军工程大学,2007.Bi Y.Finite Time Thermodynamic Optimization for Performance of Air Heat Pumps[D].Postdoctoral Report,Naval University of Engineering,2007.

[20]Bi Y,Chen L,Sun F.Heating load,heating load density and COP optimizations for an endoreversible air heat pump[J].Appl.Energy,2008,85(7):607-617.

[21]毕月虹,尚春鸽,王欣红,等.空气热泵的供热率密度分析与优化[J].北京工业大学学报,2009,35(增刊.):74-78.Bi Y,Shang C,Wang X,Liu Y.Analysis and Optimization of Heating Load Density for an Air Heat Pump[J].J.Beijing University of Technology,2009,35(Supp.):74-78.

[22]Bi Y,Chen L,Sun F,et al.Exergy-based ecological optimization for an endoreversible air heat pump cycle[J].Int.J.Ambient Energy,2009,30(1):45-52.

[23]Bi Y,Chen L,Sun F.Comparative performance analysis for endoreversible simple air heat pump cycles considering ecological,exergetic efficiency and heating load objectives[J].Int.J.Exergy,2009,6(4):550-566.

[24]Bi Y,Chen L,Sun F.Heating load,heating load density and COP optimizations for an endoreversible variable-temperature heat reservoir air heat pump[J].Journal of Energy Institute,2009,82(1):43-47.

[25]Bi Y,Chen L,Sun F.Exergy-based ecological optimization for an endoreversible variable-temperature heat reservoir air heat pump cycle[J].Rivista Mexicana de Fisica,2009,55(2):112-119.

[26]Erbay L B,Yavuz H L.Maximum heating density of a Stirling heat pump[C].ECOS98,Nancy,France,533-539.