船位误差对外弹道测量及定轨精度的影响*

(中国卫星海上测控部，江苏 江阴 214431)

1 引 言

国内关于陆基测量数据的处理技术已经比较成熟，精度也比较满意。但船载无线电设备的跟踪测量是运动的测站测量运动的目标，与陆基测量相比，航天测量船测量系统数据产生的过程和工程背景要复杂得多，误差源也更多，海上测量时获取的外弹道数据中混入了更多的误差成分，船载设备外弹道测量数据处理，除了与陆基同类测量设备做类似的误差修正外，还要进行船位、船姿、船体变形等修正处理,因此其测量精度不仅与船载外测设备本身的测量精度有关，而且与测量船船位、船体姿态、船体变形、船位船速测量等精度有关[1-2]。因此，有必要针对不同误差源对测轨结果的影响进行分析。本文针对船位误差，分析其对测轨结果的影响。

2 船位误差对测量船外测数据的影响

在测量船上，集中了众多的测量设备，担任外测任务的主要测量设备有船载单脉冲精密跟踪测量雷达、C频段微波统一测控系统和S频段微波统一测控系统，它们的基座固联于船体甲板上，只有将其获取的测量数据转换为地平系数据，才能用于轨道计算。由于船载外测设备的数据处理[1]非本文讨论的重点，且目前C频段设备仅有三元素测量资料，以下不区分设备地针对惯导地平系三元素测量资料方位A、仰角h、斜距ρ进行讨论。

测量船船位的测量是通过高精度的惯性导航系统完成的，由于惯导测量的船位会随时间出现漂移，自“嫦娥”一号任务起，船位多由精度更为稳定的卫星导航系统提供(以下简称卫导)。

2.1 船位误差对斜距的影响

为了获得船位误差对船载外测数据的影响，必须要明确航天器、测量船测量船位与真船位之间的关系，记测量船真位置在惯导地平系中的位置矢量为r0，航天器在惯导地平系中的位置矢量为rG，航天器在真船位地平系中的位置矢量为r，3个矢量之间的关系见图1。

图1 测量船惯导原点、真船位与测量目标之间的矢量关系图

由图1可得：

r=rG-r0

(1)

利用r对点乘上式两端，得到：

R=RG·cosθ1-R0·cosθ2

(2)

式中，R、RG、R0分别为矢量r、rG、r0的模，θ1为r与rG之间的夹角，θ2为r与r0之间的夹角。

由于R0的量级在10 m级，而R和RG的量级在百公里到万公里级甚至更高，因此θ1接近0，故有：

R≐RG-R0·cosθ2

(3)

式(3)即为船位误差对目标斜距R影响的数学表达式。

2.2 船位误差对测角的影响

下面考察船位误差对测角的影响。

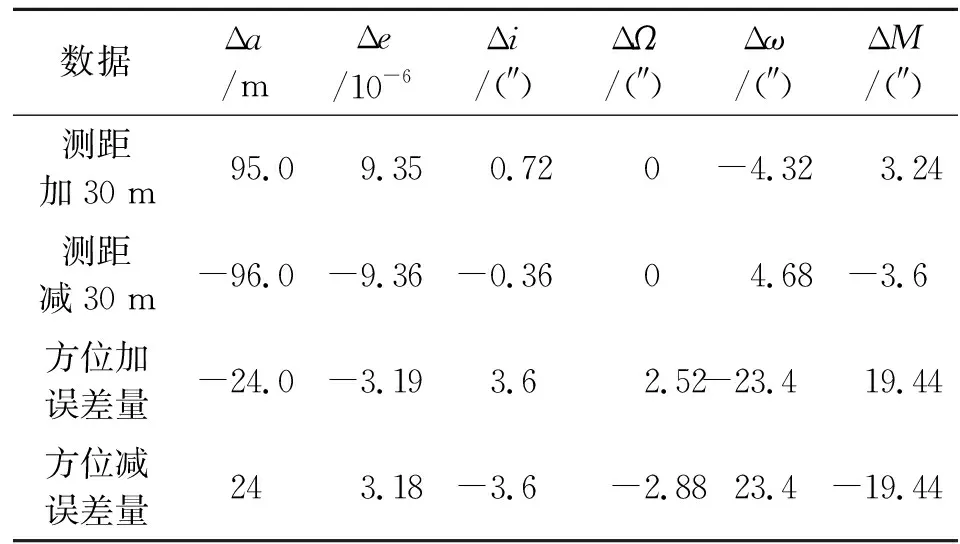
记Rd、Rg为矢量r、rG在地平系投影的模，真船位在惯导地平系中的位置矢量可以用r0=(R0,A0,h0)表示，根据余弦定理，并考虑到θ1接近0、R0<

cosh≈coshG

(4)

可知仰角基本不受船位影响。

考虑3个矢量在地平系真北方向投影的模之间的关系有：

RdcosA=RgcosAG+R0cosh0cosA0

(5)

又Rd=Rcosh，Rg=RGcoshG，因此，结合上述结论，船位对方位角的影响可表示为

(6)

从式(6)可知，船位对方位角的影响不仅与船位偏差有关，还与目标的仰角有关。

2.3 试算

由以上推理可知，船位误差对目标斜距、仰角的影响范围可以量化，而对方位的影响是无法简单估算的，下面针对保精度情况下，估算船位误差对方位的影响。

船载设备的保精度测量条件之一就是仰角的范围在7°～75°之间，假定卫导定位具有30 m的精度，则针对不同轨道高度的典型任务，方位角的误差变化范围可从表1得到。

表1 船位误差对不同高度航天器测轨结果(方位角)的影响范围

3 船位误差对测量船外测定轨的影响

船位误差对测量船外测定轨结果的影响范围可以依据上述理论推导，仿真给出。下面针对不同类型的测量任务，给出相应的影响范围。由于本文的重点是考察船位误差的影响，在仿真计算中，采用单位矢量法[3]，并且不考虑摄动模型[4]误差及摄动模型误差与船位误差的耦合效应。

以任务A、B、C的实测数据为参照，在此基础上分别考虑船位误差对斜距、方位的最大影响，计算结果见表2～4。

表2 船位误差对斜距1 000 km以下短弧段测量任务定轨结果的影响(任务A)

表3 船位误差对斜距2 000 km以下短弧段测量任务定轨结果的影响(任务B)

表4 船位误差对斜距万公里量级短弧段测量任务定轨结果的影响(任务C)

4 结果分析和讨论

通过对以上实算结果的分析可知：

(1) 测量船船位误差对测轨结果中斜距的影响范围是-δ～δ，其中δ为船载定位设备的精度；对测轨结果中仰角基本没有影响；

(2)测量船船位误差对测轨结果中方位角的影响既与观测时刻的仰角有关，又与目标的斜距有关，其影响随着斜距的增加而减小，随着仰角的增高而变大。对于斜距在1 000 km以下的目标，在仰角较高的情况下，其影响在角分量级，对测轨的影响不可忽略；

(3)从定轨结果可以看出，船位误差对斜距的影响主要体现在定轨结果中轨道半长轴上。在观测资料斜距低于1 000 km的情况下，其对轨道半长轴的影响在百米量级，对近地点幅角、平近点角的影响在角分量级，随着观测距离的增加，影响逐渐减弱；

(4)从定轨结果可以看出，船位误差对方位的影响体现在定轨结果中轨道半长轴、近地点幅角、平近点角上。在观测资料斜距低于1 000 km的情况下，其对轨道半长轴的影响在10 m量级，对近地点幅角、平近点角的影响在10″量级，随着观测距离的增加，影响逐渐减弱。

5 结束语

综上所述，船位误差是船载测量系统的重要系统误差源之一，在观测距离较近的情况下(如目标斜距在2 000 km以内，仰角较高)，其对测定轨的影响不可忽略。随着我国“北斗”导航系统的日渐成熟，利用船载“北斗”接收机定位数据与卫导数据进行融合，可以提高船载定位系统的精度和稳定性，从而提高测量船的测控能力。此外，在有较多观测资料的情况下，利用自校准技术[5]对站址误差进行估计和修正等“软方法”，也是提高测量船测量精度的有效途径。

参考文献：

[1] 张忠华．航天测量船船姿数据处理方法[M].北京：国防工业出版社,2009.

ZHANG Zhong-hua. The data processing method of TT&C ship′s deformation[M]. Beijing: National Defense Industry Press,2009. (in Chinese)

[2] 李晓勇,张忠华,何晶.船体变形对航天测量船外弹道测量的影响[J].飞行器测控学报,2006,25(3):7-12.

LI Xiao-yong, ZHANG Zhong-hua, HE Jing. The effects of spacecraft TT&C ship′s deformation on its outer-trajectory measurement data[J].Journal of Spacecraft TT&C Technology,2006,25(3):7-12.(in Chinese)

[3] 茅永兴．航天器轨道确定的单位矢量法[M].北京：国防工业出版社,2008.

MAO Yong-xing. The unit vector method on Orbit Determination of Spacecraft[M]. Beijing: National Defense Industry Press,2008. (in Chinese)

[4] 刘林.航天器轨道理论[M].北京：国防工业出版社，2000.

LIU Lin. Theory of spacecraft orbit[M]. Beijing: National Defense Industry Press,2000. (in Chinese)

[5] 刘利生,吴斌,杨萍.航天器精确定轨与自校准技术[M].北京:国防工业出版社, 2005.

LIU Li-sheng, WU Bin, YANG Ping. Spacecraft accurate orbit-determination and self calibration technology[M]. Beijing: National Defense Industry Press,2005. (in Chinese)