改进的Loran-C同步干扰抑制高效自适应算法*

李 岩1，熊 伟1，梁 青2，胡永辉

(1.空军工程大学 电讯工程学院,西安 710077；2.西安邮电学院 电子与信息工程系,西安 710061；3.中国科学院 国家授时中心,西安 710600)

1 引 言

时间统一是运载火箭发射、火箭发动机点火与关机、多级火箭级间分离、航天器入轨必不可少的条件。靶场时统就是因国防科研试验的需要而发展起来的一门新技术，它通过授时台使国防科研试验的所有设备统一时间尺度，实时精确地控制飞行目标[1]。Loran-C授时定位系统在大型航天试验的时间和频率同步问题方面起了重要的作用。由于Loran-C信号在空间传播的过程中，除受到大气噪声、天波的干扰外，还受到同步干扰，严重影响了该系统的授时定位精度[2]。目前，主要采用自适应技术来抑制同步干扰，针对常用自适应算法存在运算量较大的缺点，本文提出了BMMax-NLMS(Block M Max Normalized Least Mean Square)算法，有效地减少了运算量。计算机仿真证明该算法能够在抑制同步干扰的同时减少运算量，最后通过对实测数据的仿真验证了这些结论。

2 Loran-C信号模型

Loran-C系统的载频为100 kHz，99%的能量集中在90～110 kHz的带宽内，采用多脉冲、相位编码发播体制，是一种脉冲式双曲线无线电导航定位系统。通常是以发射天线底部的电流波形来定义脉冲波形的，天线底部电流i(t)的时域表达式为

(1)

式中,A为天线电流峰值幅度的归一化值，单位为A；t为时间，单位为μs；τd为包周差(ECD),单位为μs；Pc是相位编码，等于0或π。

接收到的信号除含有沿地面传播的Loran-C信号xg(地波)，还包括由电离层反射的Loran-C信号xs(天波)、连续波干扰信号S(t)和噪声e(t)，则Loran-C接收机接收到的实际信号xc(t)为

xc(t)=xg(t-τd)+xs(t-τ)+S(t)+e(t)

(2)

式中,τ为天波的延迟时间。

连续波干扰S(t)根据干扰信号的频率和Loran-C信号频谱的关系又可分为同步干扰、准同步干扰和异步干扰。令同步干扰为ssi,准同步干扰和异步干扰为soi，则：

(3)

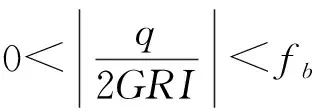
通常采用带通滤波器或脉冲累加和平均的方法来抑制连续波干扰和频带外的噪声[4]，但这些方法都只能够抑制连续波干扰中准同步干扰和异步干扰，对同步干扰的抑制效果非常有限，而同步干扰在时间测量中会引起固定的时差，还会引起Loran-C脉冲包络的变形从而导致周期识别的误差[5]，影响定位的精度。脉冲累加和平均的方法还会降低数据在接收机中的更新速度，从而降低了接收机的实时性，也限制了Loran-C接收机在其它领域中的应用。目前一种较为有效的解决办法就是运用自适应滤波技术来抑制同步干扰。

3 改进的自适应算法

人们通过研究自适应算法发现均方误差对部分滤波器系数的变化不敏感，则在迭代过程中不改变这些系数可减少运算量，T.Aboulnasr等人提出MMax-NLMS算法[6]。但该算法在选择更新系数时运算量较大[7],针对此问题本文提出BMMax-NLMS 算法,可进一步减少运算量。

3.1 BMMax-NLMS算法

该算法使用最小均方准则(MSE)，即使滤波器实际输出y(n)=xT(k)ω(k)与期望响应d(k)之间的均方误差E{|e(k)|2}为最小。令：

e(k)=d(k)-ωT(k)x(k)

(4)

式中，x(k)=[x(k),…,x(k-N+1)]T为输入向量，ω(k)=[ω0(k),…,ωN-1(k)]T为抽头权向量(滤波器系数)。

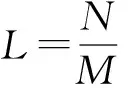
(5)

令i表示块的下标，则时刻k第i块的输入向量为

[x(k-i+1),x(k-i+2)，…，x(k-i+M)]T

(6)

分别对每块内的数据取绝对值求和，选择最大的块，令：

(7)

由qi(k)构建对角矩阵，令：

(8)

令μ为步长，δ为调整参数，则BMMax-NLMS 算法的递归表达式为

(9)

3.2 运算量比较

文献[8]中比较了NLMS算法和MMax-NLMS算法的运算量，可以看出MMax-NLMS算法有效减少了运算量。本文提出的BMMax-NLMS算法在选择系数时运用分块求和比较的方法将MMax-NLMS算法的运算量进一步减少，运算量比较见表1。

表1 两种算法运算次数比较

4 仿真实现

构建Loran-C信号模型，假设地波延迟100 μs，天波延迟160 μs，天波相对地波的幅度比为2 dB，噪声为高斯白噪声，信噪比是-5 dB，载波干扰频率分别为77.7 kHz、100 kHz、105 kHz和115.3 kHz，采样频率为1 MHz，做1 024点的FFT变换。通过Matlab仿真，得到叠加干扰的Loran-C信号的频谱如图1所示。

图1 叠加干扰的Loran-C信号频谱

运用BMMax-NLMS算法对叠加干扰的Loran-C信号进行滤波，假设滤波器的阶数N=30，取M=10，步长μ=0.7，通过表1可以得到MMax-NLMS算法总运算次数是331次，改进算法的总运算次数是118次，运算量减少了213次。通过改进算法滤波后得到的信号频谱如图2所示。由图可见，滤波后的频谱只在100 kHz处出现了峰值，并且和标准Loran-C信号频谱重合得较好，有效抑制了同步干扰，对其它频率的干扰该算法的抑制效果也非常明显。

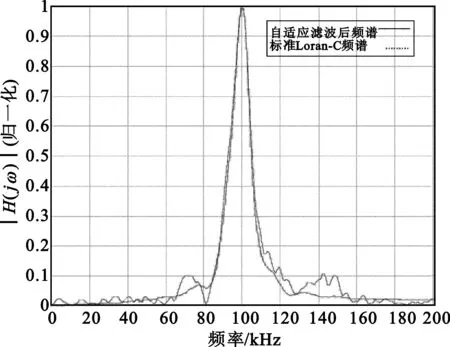
图2 滤波后的Loran-C信号频谱

5 实测数据分析

图3(a)是从国家授时中心接收由陕西蒲城发射的Loran-C信号，可以看出，Loran-C脉冲组前8个脉冲的间隔皆为1 ms，第8、9个脉冲间隔为2 ms。对接收到的实测信号进行FFT变换得到实测信号频谱，如图3(b)所示，可以看出在90～110 kHz频率范围内，出现的毛刺为同步和准同步干扰，且强度较大，而异步干扰较弱。

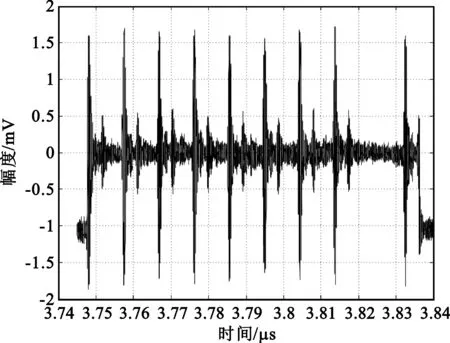
(a)实测信号波形

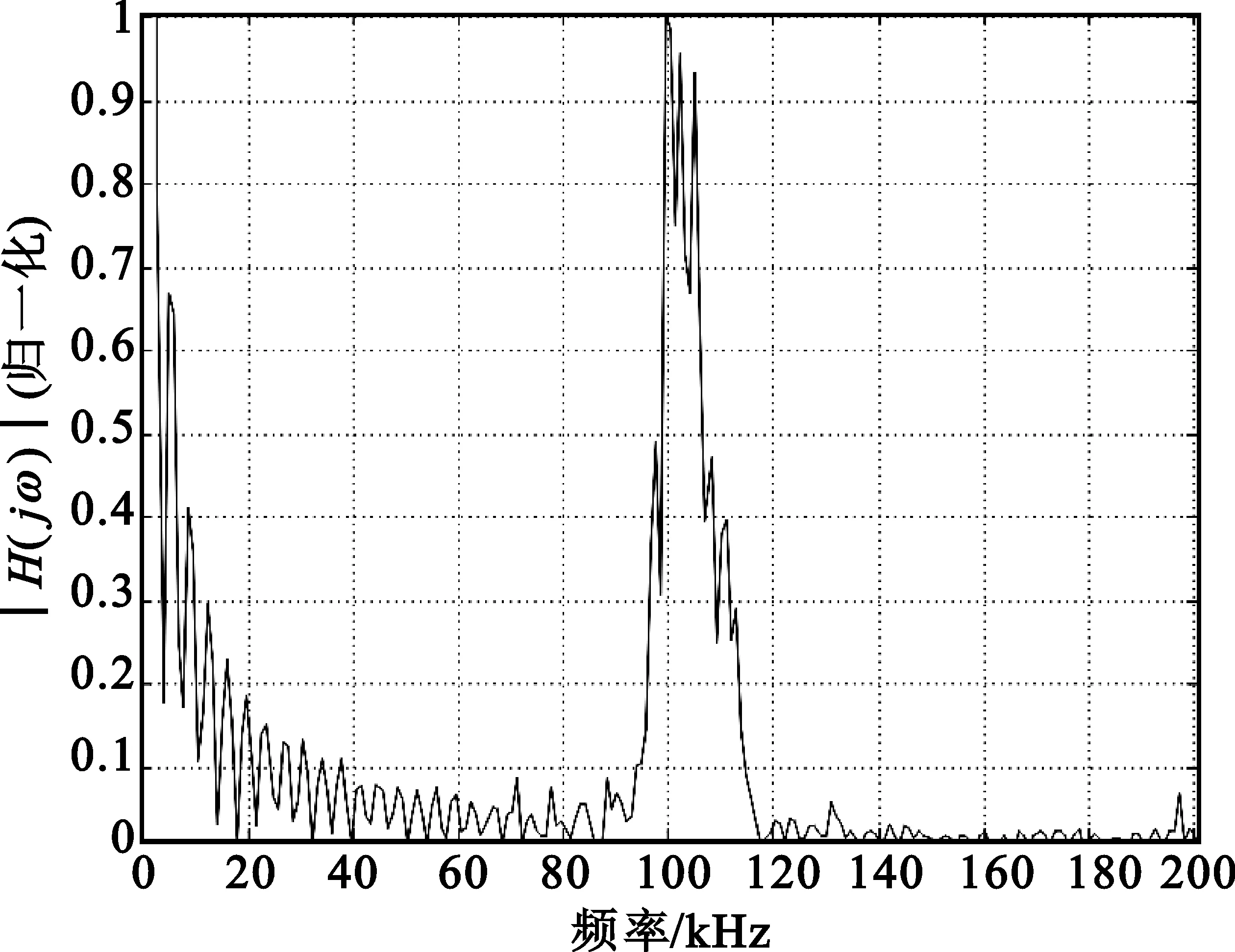
(b)实测信号频谱

截取第5个脉冲对378 300～378 900 μs的数据进行自适应滤波，改进算法的参数保持不变，实验结果如图4所示。可见，滤波后的频谱和标准Loran-C频谱基本重合，在90～110 kHz频率范围内没有出现毛刺，较好地抑制了同步和准同步干扰，只在117 kHz附近出现了波峰，但幅度较小。Loran-C频谱外的曲线幅度也很小，说明对异步干扰也起到了很好的抑制。

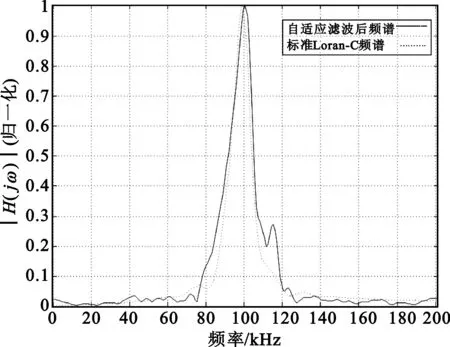
图4 滤波后输出信号频谱

6 结束语

计算机仿真和对实测数据的分析表明，利用BMMax-NLMS算法来抑制Loran-C信号的同步干扰能够有效减少运算量，并取得较好的抑制效果，对Loran-C接收机的研究具有一定的实用价值。

参考文献：

[1] 熊伟,胡永辉,钱建立,等.靶场时统中自适应Loran-C接收机的研究[J].固体火箭技术,2008,31(3):303-306.

XIONG Wei, HU Yong-hui, QIAN Jian-li, et al. Research on Loran-C adaptive receiver in range time series system[J]. Journal of Solid Rocket Technology, 2008,31(3):303-306.(in Chinese)

[2] US COAST GUARD. Loran-C User handbook[M]. Washington DC:US Coast Guard,1992.

[3] YI Bian, David Last. High-Efficiency Loran-C Interference Identification by Synchronous sampling[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997,33(1):134-141.

[4] Beckmann M.Interference detection and suppression in Loran-C receiver[J].IEE Proceedings,1989,136(6):255-261.

[5] Last D,YI Bian. Carrier Wave Interference and Loran-C Recriver Performance[J]. IEE Proceedings-F, 1993, 140(5):273-283.

[6] Aboulnasr T, Mayyas K. Complexity Reduction of the NLMS Algorithm via Selective Coefficient Update[J]. IEEE Transactions on Signal Processing, 1999, 47(5):1421-1424.

[7] Aboulnasr T, Mayyas K. MSE Analysis of The M-Max NLMS Adaptive Algorithm[C]//Proceedings of the 1998 IEEE International Conference on Acoustics,Speech and Signal Processing.Seattle:IEEE,1998:1669-1672.

[8] Andy W H Khong,Patrick A Naylor.Selective-Tap Adaptive Filtering With Performance Analysis for Identification of Time-Varying Systems[J].IEEE Transactions on Audio,Speech,and Language Processing,2007,15(5):1681-1695.