运用高阶累积量和SVM的调制自动识别
(解放军电子工程学院,合肥 230037)
1 引 言
通信信号调制模式自动识别在军用和民用方面一直发挥着重要作用。在军用方面,调制模式的正确、有效识别是指挥员制定侦察和对抗的前提条件;在民用方面,政府通信部门可以利用它进行信号确认、干扰识别和频谱监测等无线电管理工作,以防止用户对无线频谱的非法利用和干扰,保证合法通信的正常进行。
目前,数字信号调制模式自动识别主要有两种方法:决策论的识别方法和统计模式的识别方法。由于统计模式识别方法提取特征相对简单,需要的先验知识少,算法灵活,因此,很多学者采用这种方法进行调制模式自动识别研究。
调制模式识别的关键是提取性能优、稳健性好的分类特征。由于高阶累积量具有良好的抗噪性能,因此,使用高阶累积量进行模式识别的研究也越来越多。Swami利用四阶累积量实现了2PSK和4PSK信号的分类识别[1];文献[2]利用四阶、六阶累积量实现了对2ASK、4ASK、4PSK、8PSK、16QAM的识别;陆凤波利用信号差分的四阶、八阶累积量实现了4种调相信号的识别[3];文献[4]利用四阶、六阶累积量构造两个分类特征实现了6种信号的分类。
通过分析和研究,发现以上文献识别的类型相对较少,在低信噪比下识别率不高。因此,本文采用一种新的基于高阶累积量和支持向量机的识别算法,实现了2ASK、4ASK、8ASK、4PSK、8PSK、8QAM、16QAM、32QAM共8种信号在低信噪比下的有效分类。
2 高阶累积量特征提取
假设接收到的信号已经过下变频、载波同步和符号同步,此时,接收到的被噪声污染的复基带信号可表示为
r(t)=s(t)+n(t)=

(1)
式中,A为载波幅度,an为码元序列,gt为发送码元波形(矩形脉冲),θc为载波初始相位,nt为高斯白噪声信号。
2.1 高阶累积量理论基础
下面给出本文所用到的高阶累积量的定义。在介绍高阶累积量之前,先定义高阶矩。对于一个具有零均值的复随机过程Xt,p阶混合矩定义为
Mpq=EXtp-qX*tq
(2)
式中,*表示复共轭。然后定义各阶累积量[5]:
(3)
C41=M41-3M20M21
(4)
(5)
(6)
(7)
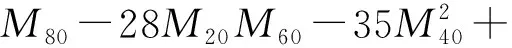
(8)
C84=M84-16C63M21-C402-
(9)
2.2 数字调制信号的高阶累计量分析
由于高斯随机过程二阶以上累积量的值为零,所以,接收到的受高斯白噪声污染的复基带信号累积量值即为原复基带信号累积量的值。假设发送的码元服从独立同分布,复基带信号经过零均值预处理和功率归一化后,将其代入到式(3)~(9)中,计算各阶累积量的值。理论计算值如表1所示。

表1 信号的高阶累积量理论值Table 1 Signals′ higher order cumulants theoretic values
在实际工程应用中,通常使用信号样本数据来估计高阶累积量的值。首先,p阶混合矩的样本估计表示式为
(10)
式中,N为样本数据点数,Xk为信号。然后,把混合矩的估计值代入到累积量公式就能得到各阶累积量的样本估计值。
2.3 构造累积量分类特征

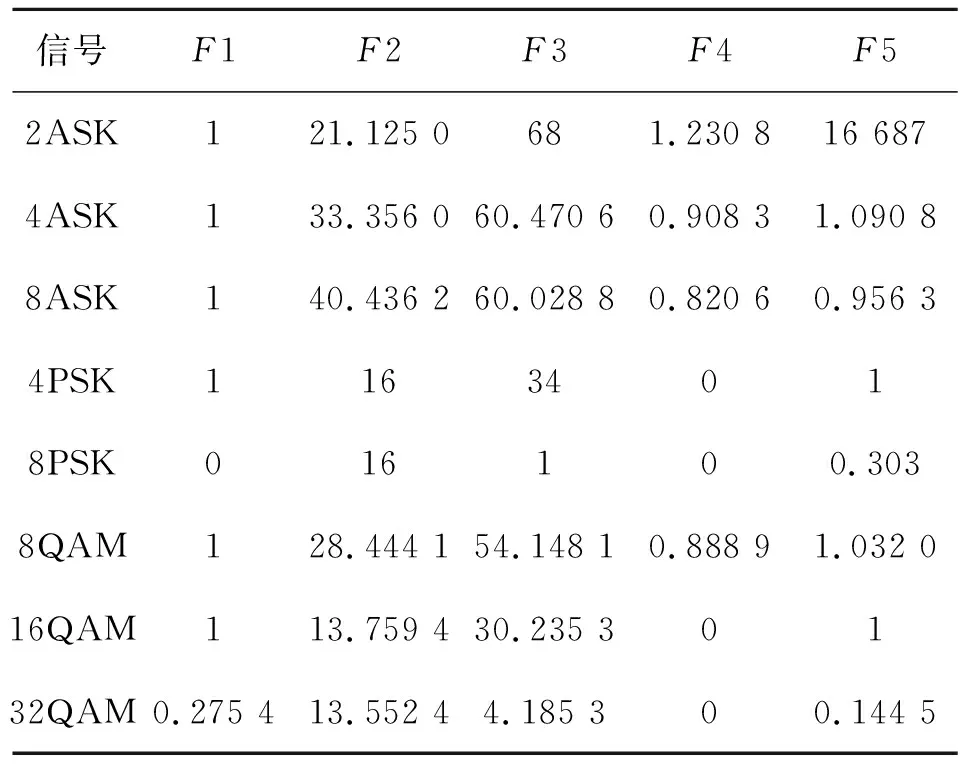
表2 信号的特征参数的理论值Table 2 The signals′ characteristic parameters theoretic values
3 二叉树结构的支持向量机分类器
二叉树结构的支持向量机是一种处理多类分类问题的高效方法,其基本思想是:从根节点开始,将该节点所包含的类别划分为两个子类,再将两个子类划分为两个次级子类,如此迭代下去,直到得到一个单独的类别为止,这样就将多类分类问题转换为两类分类问题,其中每两子类之间采用支持向量机作为分类器。通常情况下,二叉树结构的支持向量机分为两种:一种是在每个内节点处,只将一个类别与其它类别分开;另一种是在每个内节点处,将所有类别分为两类。本文采用第一种二叉树结构的支持向量机分类器,并采用一种新的类距离方法生成二叉树结构[6],其基本思想是把与其它类相隔最远的类优先分离出来。
首先,定义类距离dij为i类和j类均值向量间的距离减去各自类的平均半径,即:
dij=‖mi-mj‖2-ri-rj
(10)
(11)
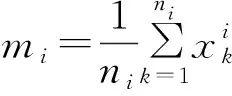
以类均值距离生成二叉树结构支持向量机的步骤如下:
第一步:运用式(10)计算类与类之间的距离;
第二步:对每一类都存在k-1个与其它类的距离值,分别对每个类的这些距离值从小到大排列,并重新编号;
第四步:根据类标号排序,生成二叉树;
第五步:根据生成的二叉树,利用二分类SVM训练算法构造二叉树内各节点的最优超平面。
该方法解决了不可分盲点、传统结构识别率不够优等问题,提高了算法的性能,具有较好的推广性。
4 实验性能分析
本文所研究的待分类调制信号为2ASK、4ASK、8ASK、4PSK、8PSK、8QAM、16QAM、32QAM;仿真环境为加性高斯白噪声信道;载波频率fc=1 000 Hz,采样频率fs=8 000 Hz,码元速率f=1 000 bit/s,每个样本2 000个采样点,用于二叉树结构的支持向量机分类器的样本数为150个,其中,50个样本用于训练,100个样本用于测试性能,以上参数在后面的仿真和性能测试中均保持不变。
4.1 特征参数随信噪比变化
对5个构造的新的分类特征随信噪比变化情况进行仿真。8种信号,信噪比从0~20 dB以间隔1 dB变化,各取100个样本,计算特征参数的均值。仿真结果如图1所示。
从图1可看出,变化曲线之间能够较好地区分,即说明8种信号能够通过5个新的分类特征进行识别,为采用支持向量机进行识别提供了依据。
4.2 识别性能
本文采用Monte Carlo仿真实验的方法来分析算法的性能。通过两个仿真实验的对比来验证算法的有效性,即基于高阶累积量与二叉树结构的支持向量机识别算法和基于高阶累积量与直接多类分类支持向量机的算法。仿真实验中所用的参数均一致,信噪比从0~20 dB以间隔5 dB变化;SVM采用径向基核函数,核函数参数δ2=0.001 5,惩罚因子C=650。
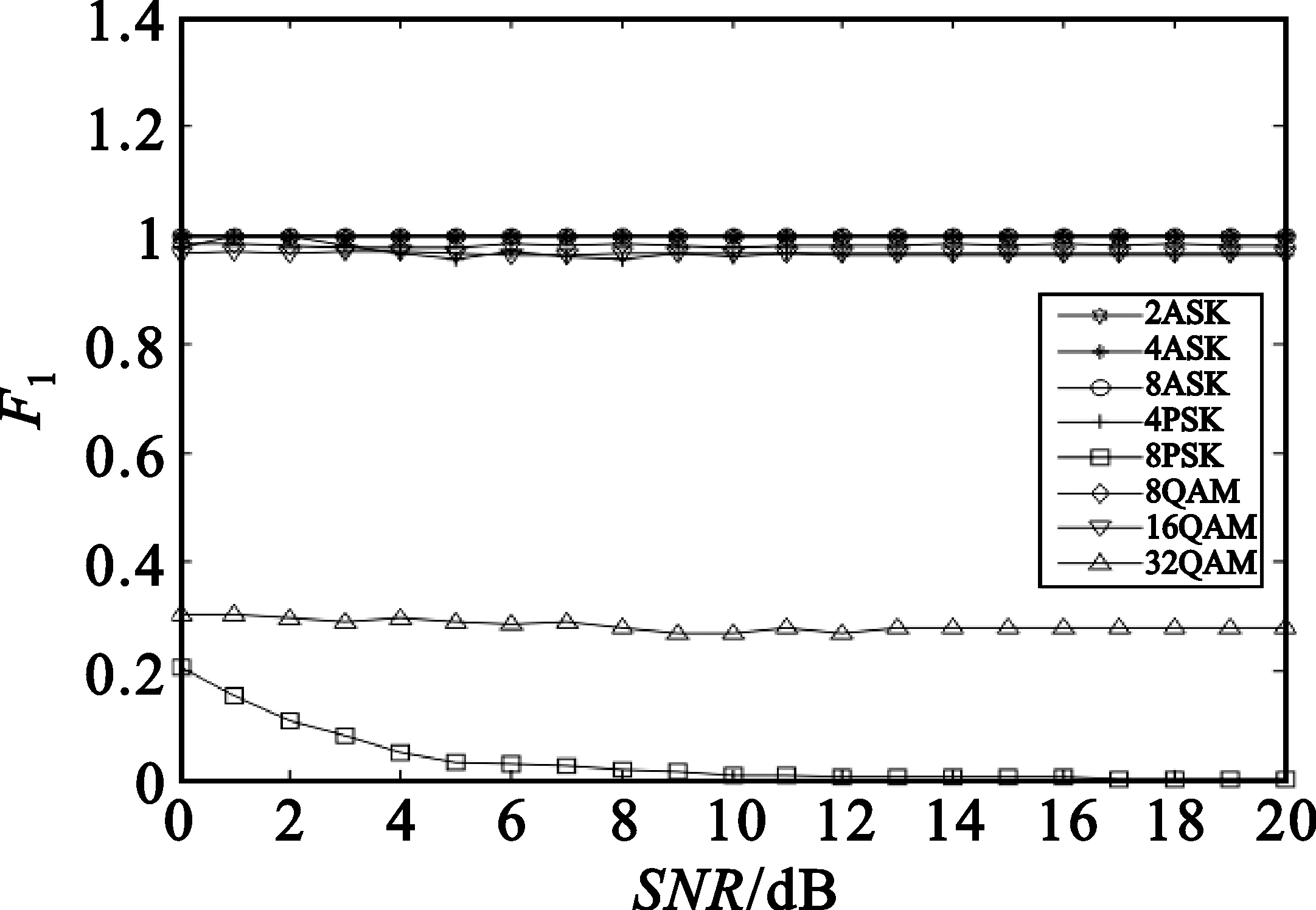
(a)参数F1随信噪比变化曲线
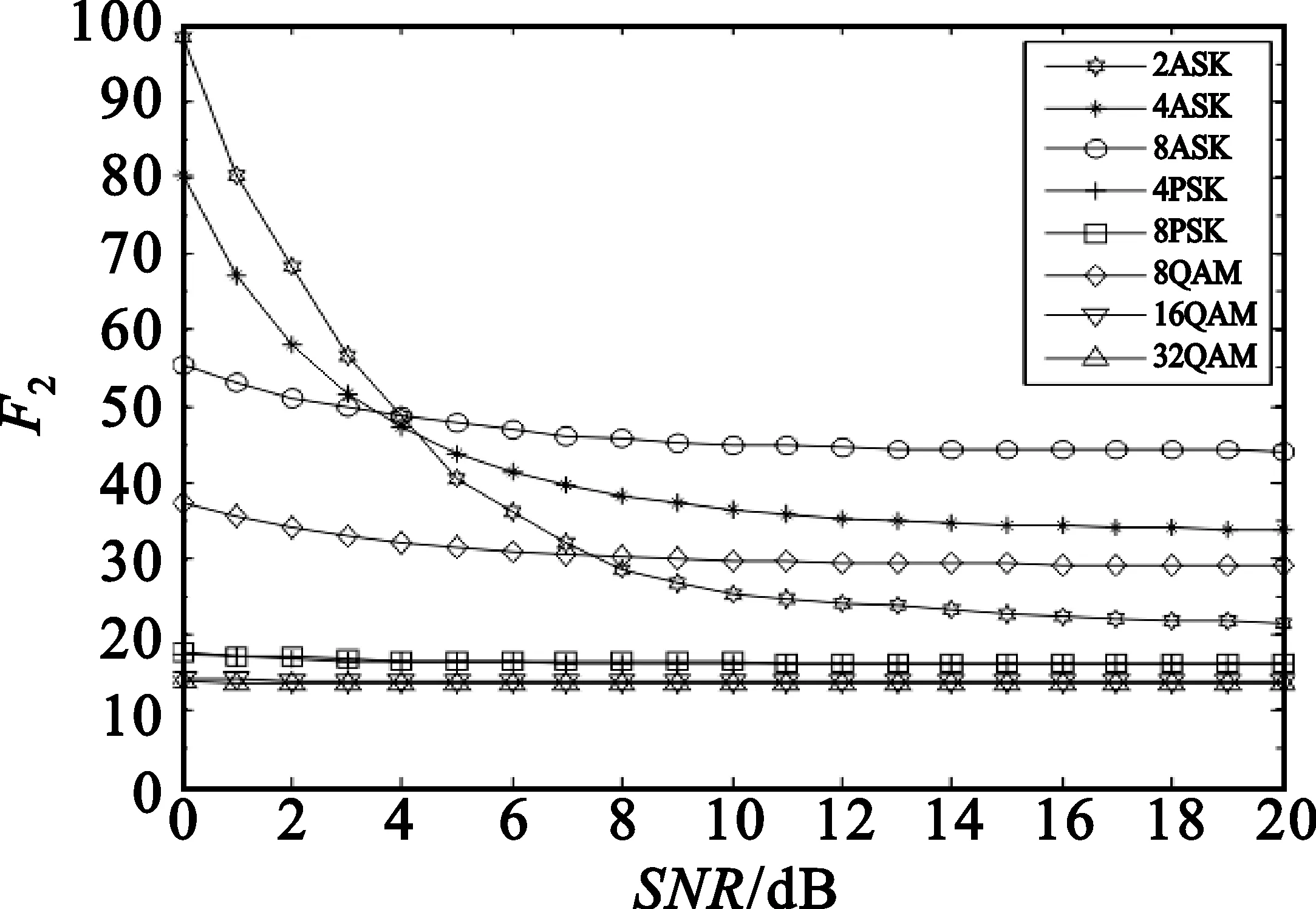
(b)参数F2随信噪比变化曲线
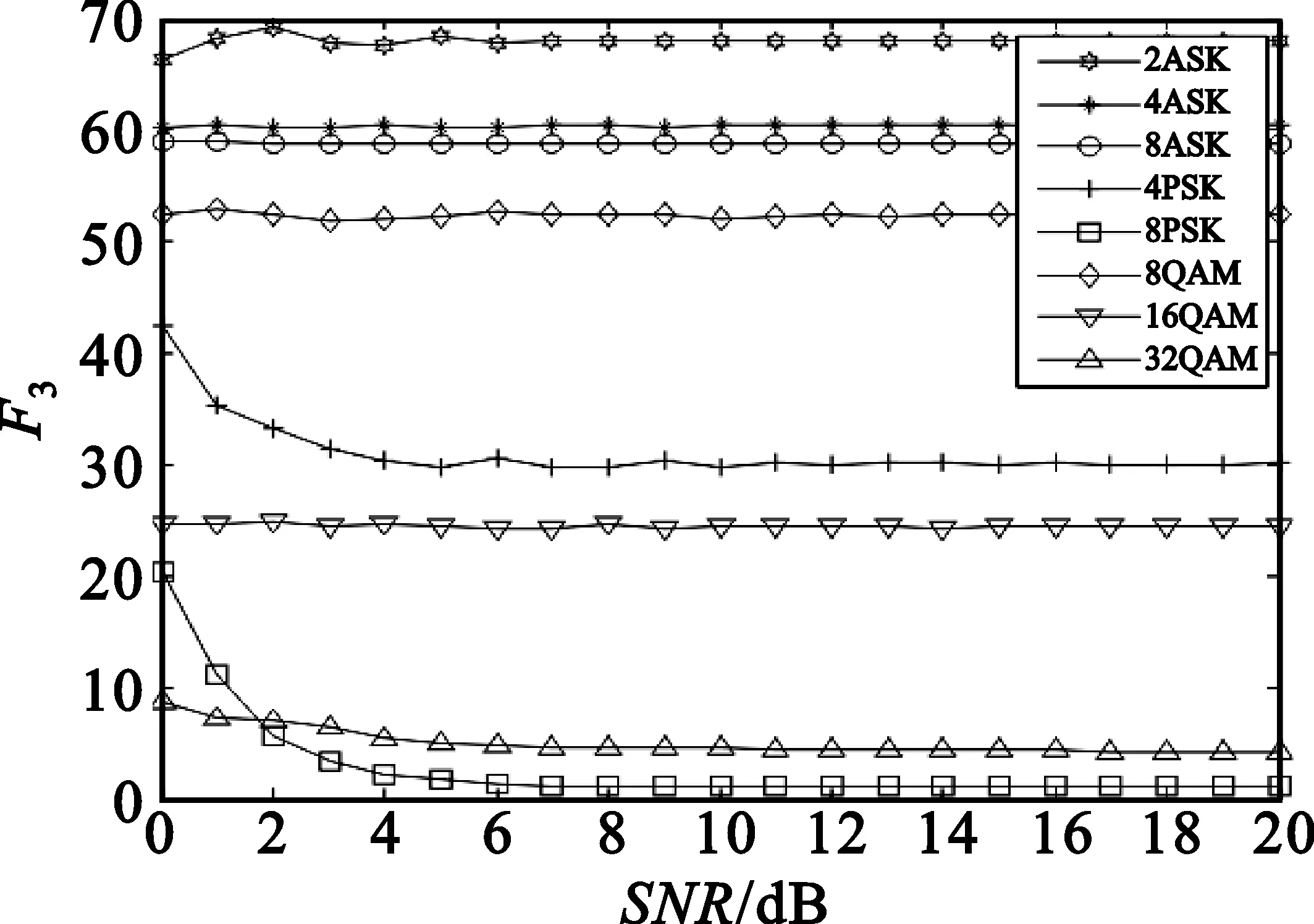
(c)参数F3随信噪比变化曲线

(d)参数F4随信噪比变化曲线

(e)参数F5随信噪比变化曲线图1 特征参数随信噪比变化曲线Fig.1 Characteristic parameters versus SNR
仿真实验1:基于高阶累积量与直接多类分类支持向量机算法仿真。仿真结果如表3所示。
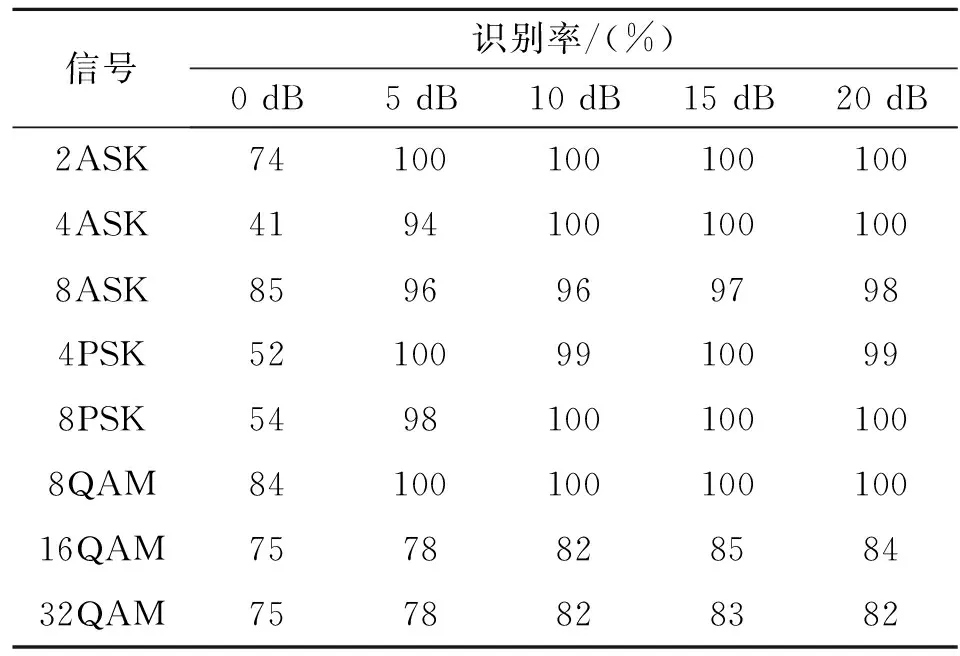
表3 直接多类分类SVM识别率仿真结果Table 3 The recognition rate based on direct SVM
仿真实验2:本文算法仿真,即高阶累积量与二叉树结构的支持向量机算法仿真。根据本文所研究识别信号的特点和构造的5个特征参数随信噪比变化情况,可得到该算法的识别流程图,见图2。

图2 信号识别流程图Fig.2 The identification flowchart of signals
依据图2流程进行仿真,仿真结果见表4。
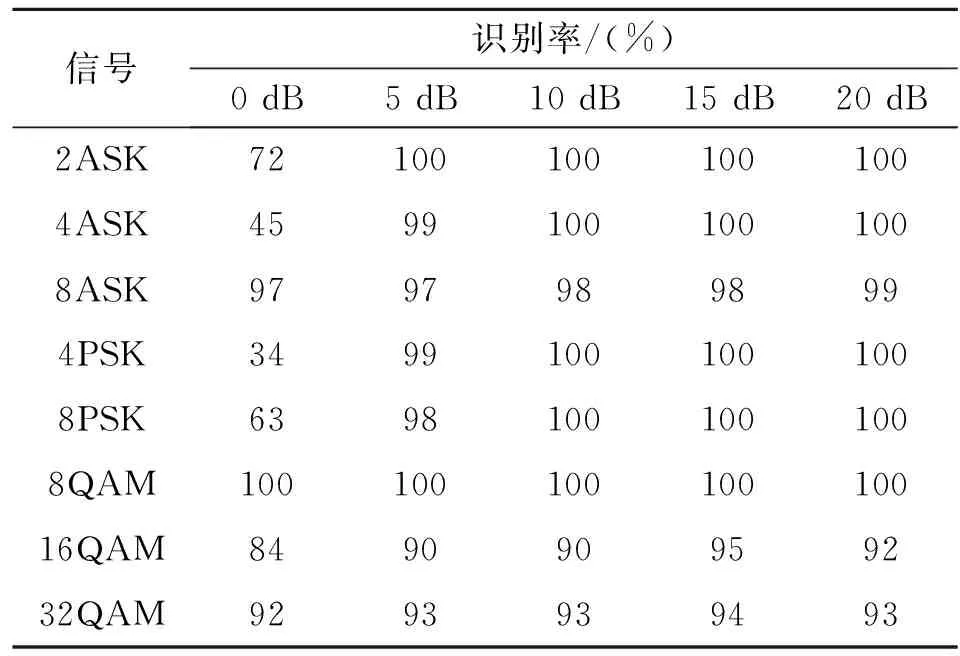
表4 基于二叉树结构的SVM识别率仿真结果Table 4 The recognition rate based on BT-SVM
从表3和表4的仿真结果来看,基于高阶累积量与直接多类分类支持向量机算法在信噪比大于5 dB时,总体识别率78%以上,当信噪比为0 dB时,8种信号识别率较低;本文算法在信噪比大于5 dB时,总体识别率在90%以上,除16QAM和32QAM外,其它信号识别率接近100%。
5 结 论
本文通过对高阶累积量理论的研究和待识别信号的分析,提出了5个新的分类特征,这5个特征对信号的尺度大小和相位变化具有很好的稳健性,再结合二叉树支持向量机对所研究信号进行识别,通过仿真验证,证明了本文算法的有效性。但本文算法在信噪比低于5 dB时,对2ASK、4ASK、4PSK、8PSK 4种信号识别率较低,比较难区分,在后续研究中要深入分析进行解决。且本文算法仅是在高斯白噪声信道下进行验证的,而实际信道环境比较复杂,如何将该算法推广、应用到实际复杂的信道环境下,也是今后研究的方向。
参考文献:
[1] Swami A, Sadler B M. Hierarchical Digital Modulation Classification Using Cumulants[J].IEEE Transactions on Communication,2000,48(3):416-429.
[2] 韩钢,张文红,李建东,等.基于高阶累积量和支撑矢量机的调制识别研究[J]. 系统工程与电子技术,2003,25(8):1008-1011.
HAN Gang, ZHANG Wen-hong, LI Jian-dong,et al. Study on the recognition based on higher order cumulants and SVM[J]. Journal of Systems Engineering and Electronics. 2003,25(8):1008-1011. (in Chinese)
[3] 陆凤波,黄知涛,易辉荣,等.一种基于高阶累积量的数字调相信号识别方法[J].系统工程与电子技术,2008,30(9):1612-1615.
LU Feng-bo, HUANG Zhi-tao, YI Hui-rong, et al. Recognition algorithm of phase shift keying signals by higher order cumulants[J]. Journal of Systems Engineering and Electronics,2008,30(9):1612-1615. (in Chinese)
[4] WANG Lan-xun, REN Yu-jing, ZHANG Rui-hua. Algorithm of digital modulation recognition based on support vector machines[C]//Proceedings of 2009 International Conference on Machine Learning and Cybernetics.Baoding:IEEE,2009:980-983.
[5] 陈莜倩,王宏远.基于联合特征向量的自动数字调制识别算法[J].计算机应用研究,2009,26(7):2478-2480.
CHEN Xiao-qian, WANG Hong-yuan. Automatic digital modulation classification algorithm based on novel combined feature vector[J].Application Research of Computers,2009,26(7):2478-2480. (in Chinese)
[6] 吕晓丽,李雷,曹未丰.基于二叉树的SVM多类分类算法[J].信息技术,2008(4):1-3.
LV Xiao-li, LI Lei, CAO Wei-feng. SVM multi-class classification based on binary tree[J].Journal of Information Technology,2008(4):1-3.(in Chinese)

