基于OMP分解的宽带Chirp信号多参数估计
(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)
1 引 言
宽带Chirp信号作为一种大的时间带宽积信号,广泛应用于各种信息系统,如通信、雷达、声纳和地震勘探等[1],它也是一种特殊的非平稳信号。在这类系统中,Chirp信号的检测、参数和波达方向角的估计是一个重要的研究课题。
关于Chirp信号的参数估计,比较有代表性的是基于空间时频分布(STFD)的方法[2-3]。该类方法通过计算阵元间的互Wigner-Ville分布(WVD)构造时频域数据向量,然后利用Chirp信号的局部窄带特性,截取时频分布谱峰附近的时频点,对截取出的时频点数据进行特征值分解,再利用子空间类方法[4-5]实现信号参数估计。但是,该类算法只在信噪比较高的情况下才能有较好的性能,而且在多目标的情况下,信号之间的交叉项将严重影响Chirp信号的参数估计性能,弱目标很容易被交叉项所掩盖。
对于稀疏分解在阵列信号处理领域中的应用,已经有人把稀疏分解中常用的匹配追踪(MP)算法[6]引入到阵列信号处理领域中,实现了对信号参数和波达方向角的估计。而本文提出的基于正交匹配追踪(Orthogonal Matching Pursuit,OMP)[7]分解的宽带Chirp信号多参数估计方法与MP算法相比有更好的收敛性,在一定的过完备原子库密度条件下,本文所述算法能很好地实现对Chirp信号起始频率和调频斜率的估计,且波达方向角(DOA)估计的性能高于WVD算法[8],尤其在多信源和低信噪比情况下,算法仍然有良好的性能。
2 信号数学模型
假设M元线阵沿x轴均匀放置,阵元间距为d。第一个阵元位于坐标原点,称为参考阵元。假定有P个宽带Chirp信号从不同方向入射到M元阵列上,则第m个阵元的输出为
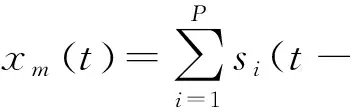
(1)
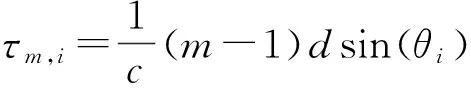
(2)

将式(2)代入式(1)可得:
(3)
(4)
将其写为向量形式可以得到阵列瞬时窄带模型:
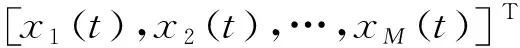
Aθ,tSt+Nt
(5)
式中,A(θ,t)=[a1(θ,t),a2(θ,t),…,aP(θ,t)]为M×P的阵列方向矩阵,包含了信源的方位信息,ai(θ,t)=[1,e-j2π(fi,0+kit)τ2,i,e-j2π(fi,0+kit)τ3,i,…,e-j2π(fi,0+kit)τM,i]T;P×1的入射信号向量为S(t)=[s1(t),s2(t),…,sP(t)]T;N(t)=[n1(t),n2(t),…,nM(t)]T为M×1的加性噪声向量。
假设取N次快拍,问题就变为在已知x(n),n=1,2,3,…,N的情况下,估计信号参数(fi,0,ki,θi),i=1,2,3,…,P。
3 基于OMP分解的宽带Chirp信号多参数估计
给定一个集合D={gk,k=1,2,3,…,K},其元素是张成整个Hilbert空间H=RN的单位矢量,K>>>N,我们称集合D为原子库,其元素为原子。集合Γ={γk,k=1,2,3,…,K}为原子参数组成的集合,其元素γk为每个原子的参数。
假设在D中所有原子的范数都为一,算法在初始化时,设R0x=x,可以首先对信号x进行第一次OMP分解,从过完备库中选出与信号x最为匹配的原子gγ0,即:
R0x=〈R0x,gγ0〉gγ0+R1x
(6)
式中,〈R0x,gγ0〉gγ0是R0x对gγ0的投影,R1x是剩余量。显然,gγ0是与R1x正交的,所以可得到下式:
‖R0x‖2=〈R0x,gγ0〉2+‖R1x‖2
(7)
初始化u0=gγ0,对m≥0,OMP挑选gγm,使得:
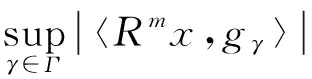
(8)
利用Gram-Schmidt算法[8]将gγm关于gγp0≤p≤m正交化,定义:
(9)
对um归一化:
(10)
将余项Rmf投影到um(而不是gγm)上,得到:
Rmx=〈Rmx,um〉um+Rm+1x
(11)
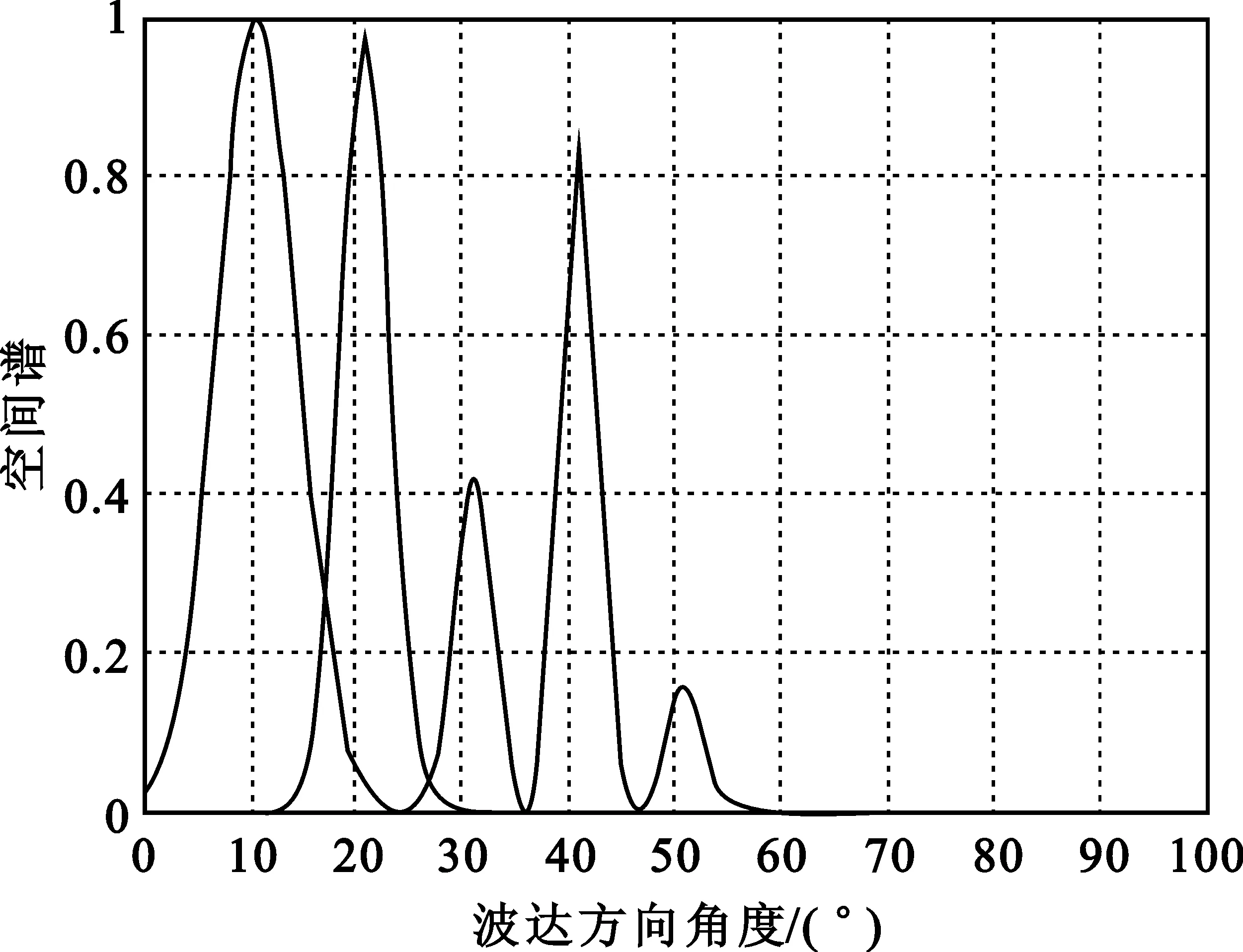
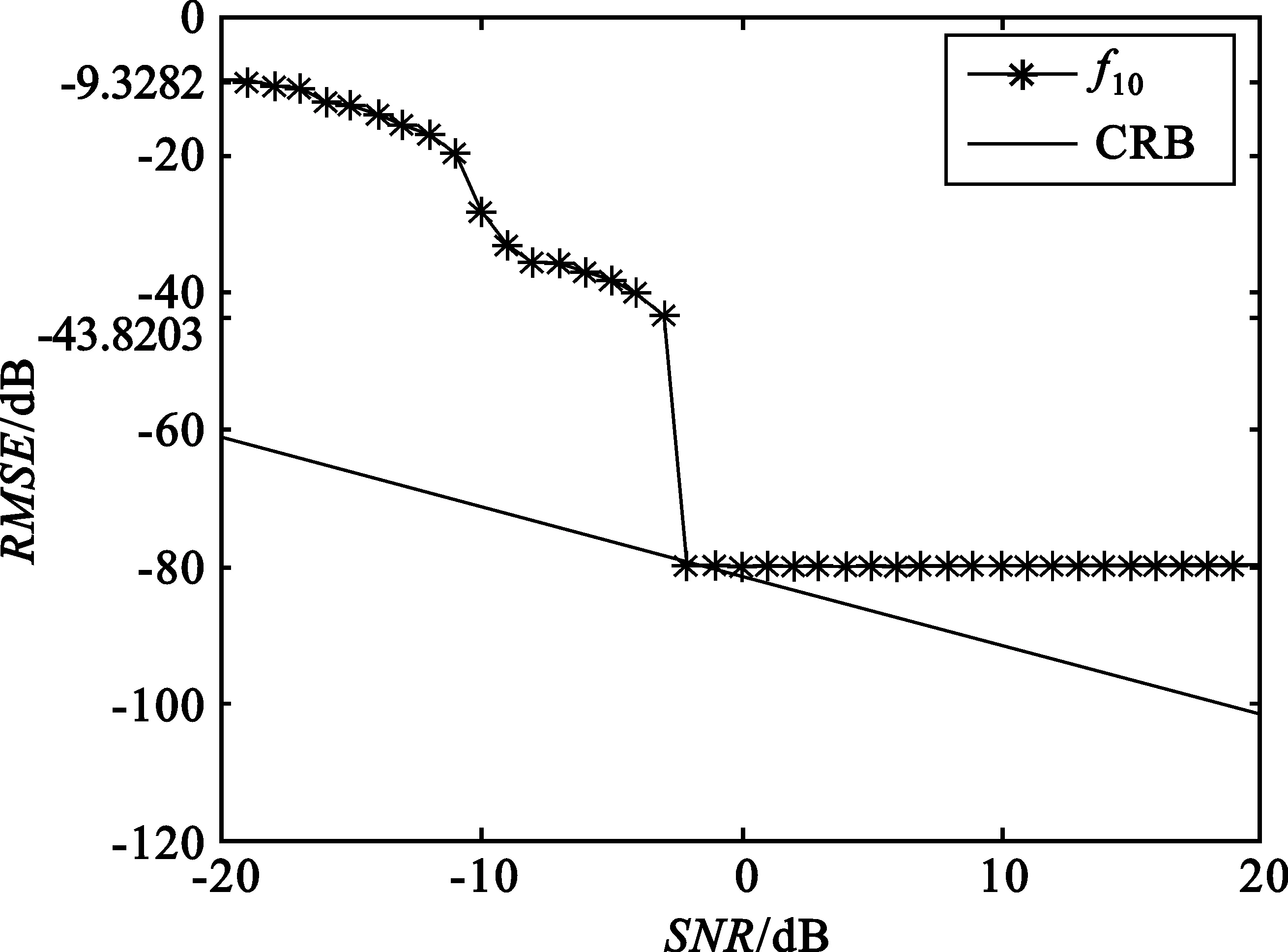
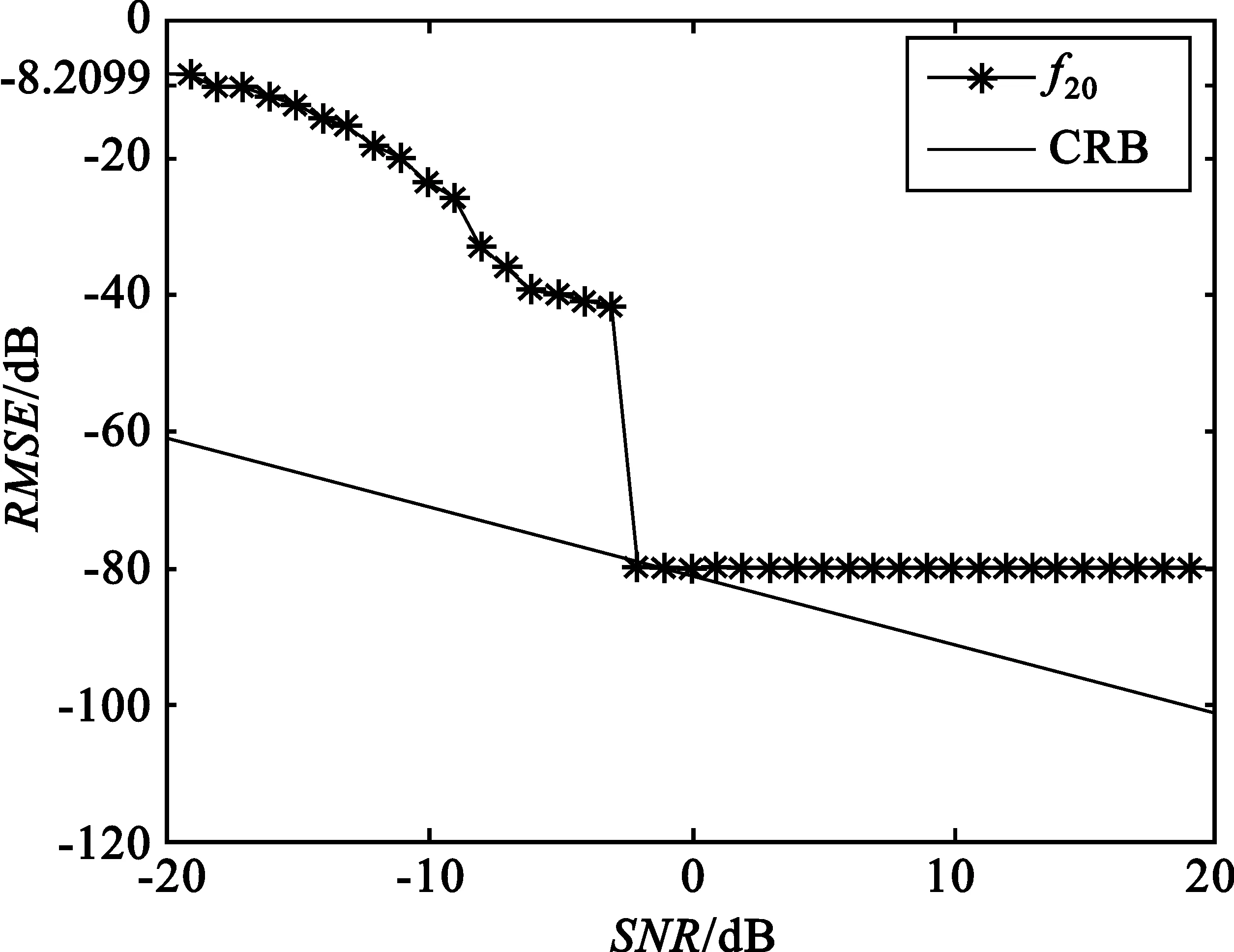
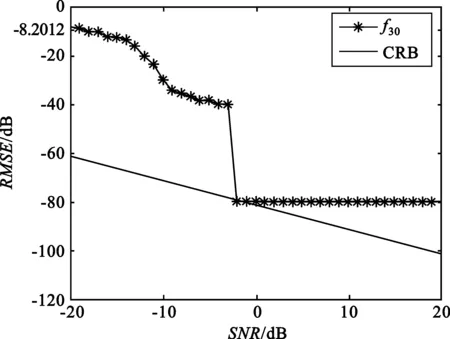
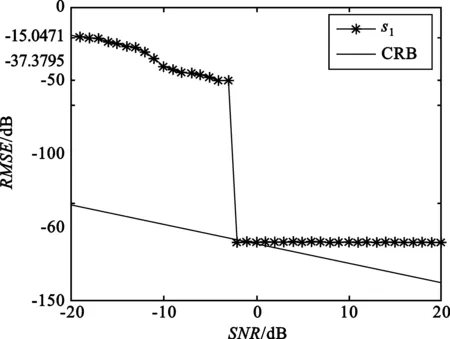
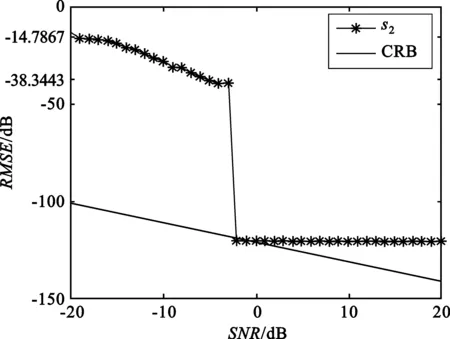
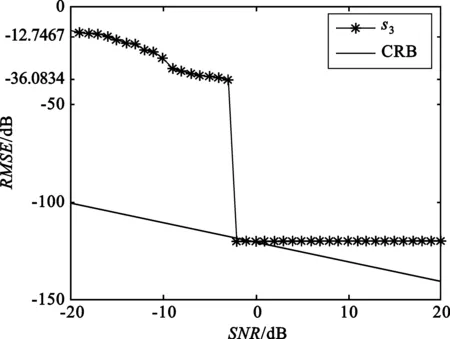
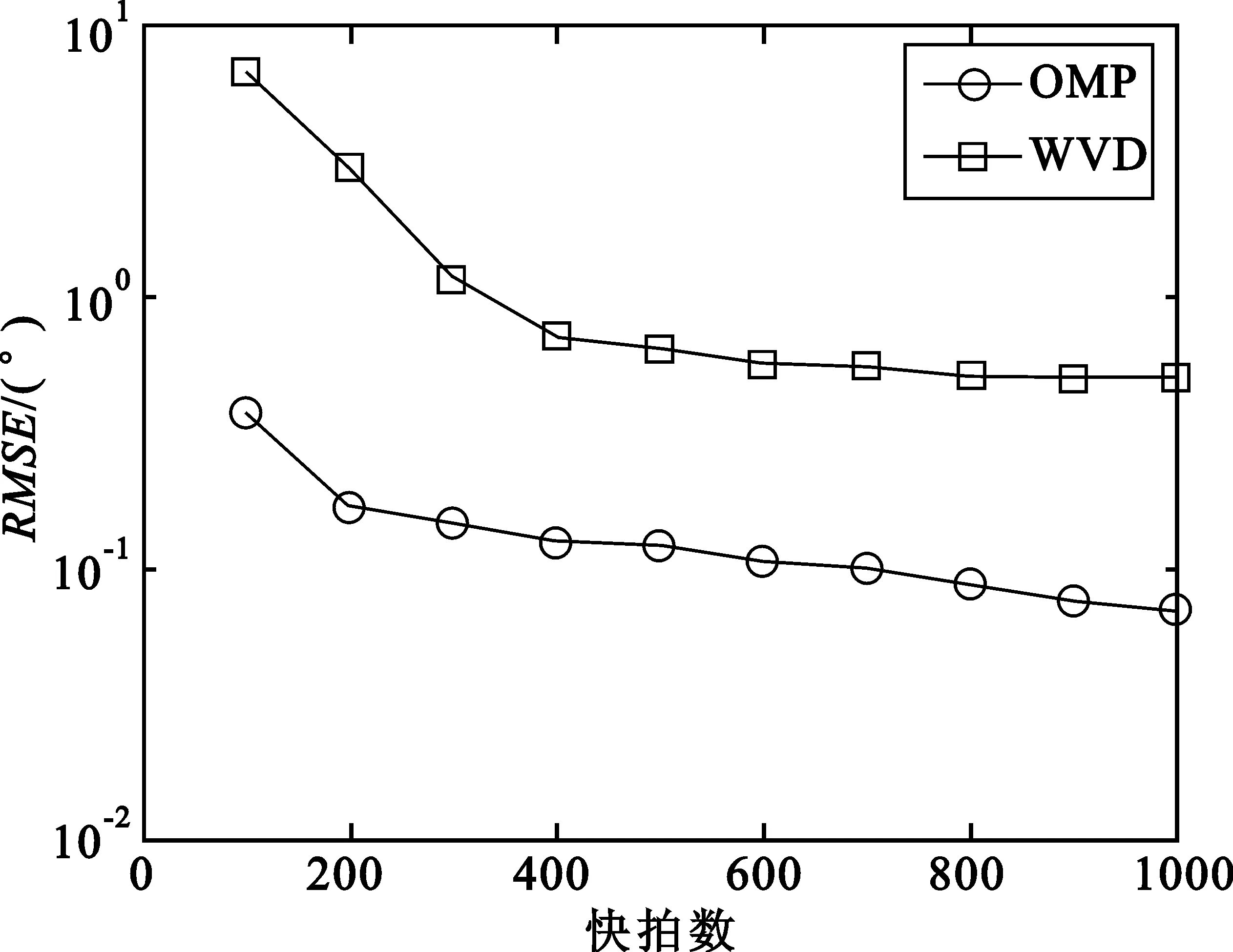
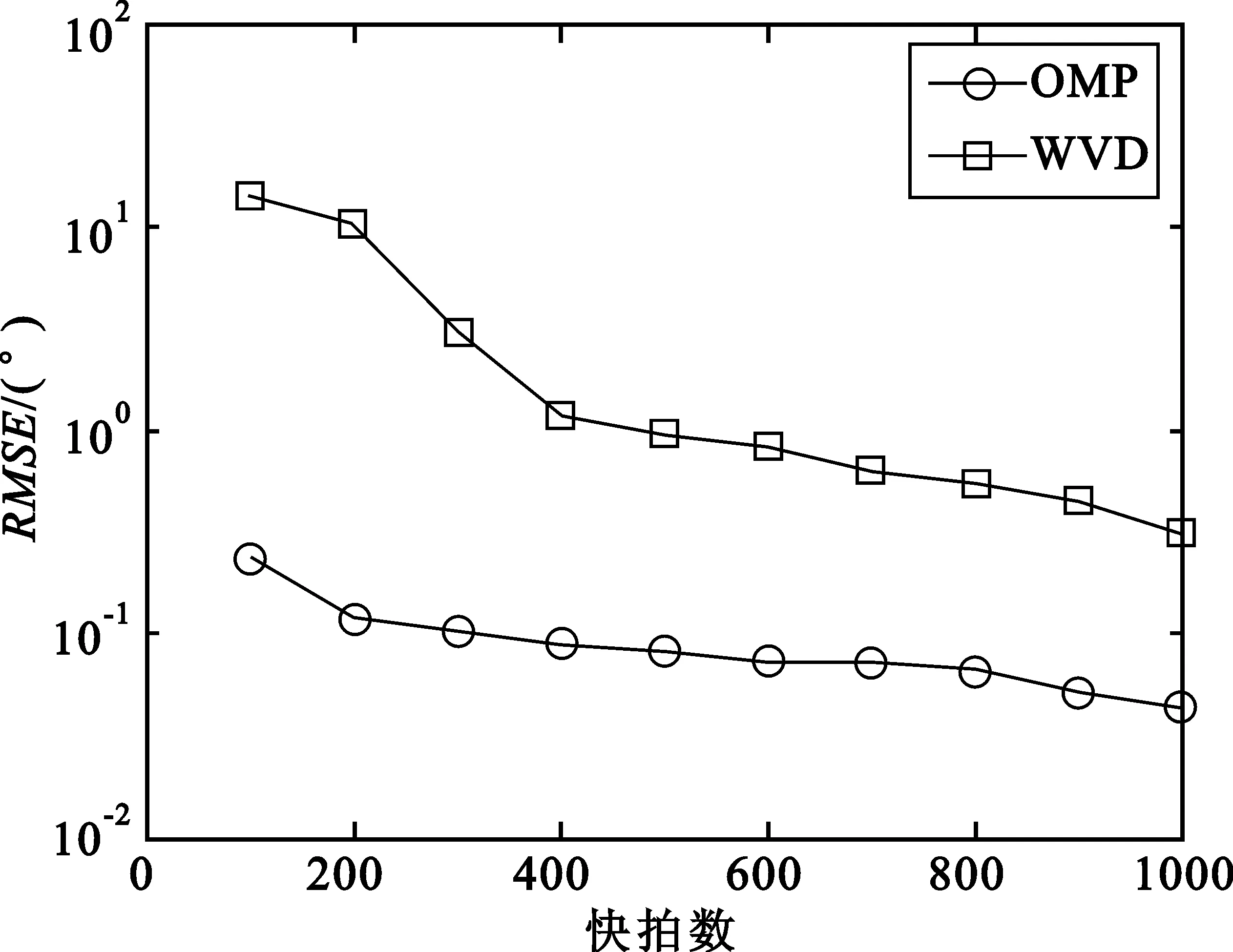
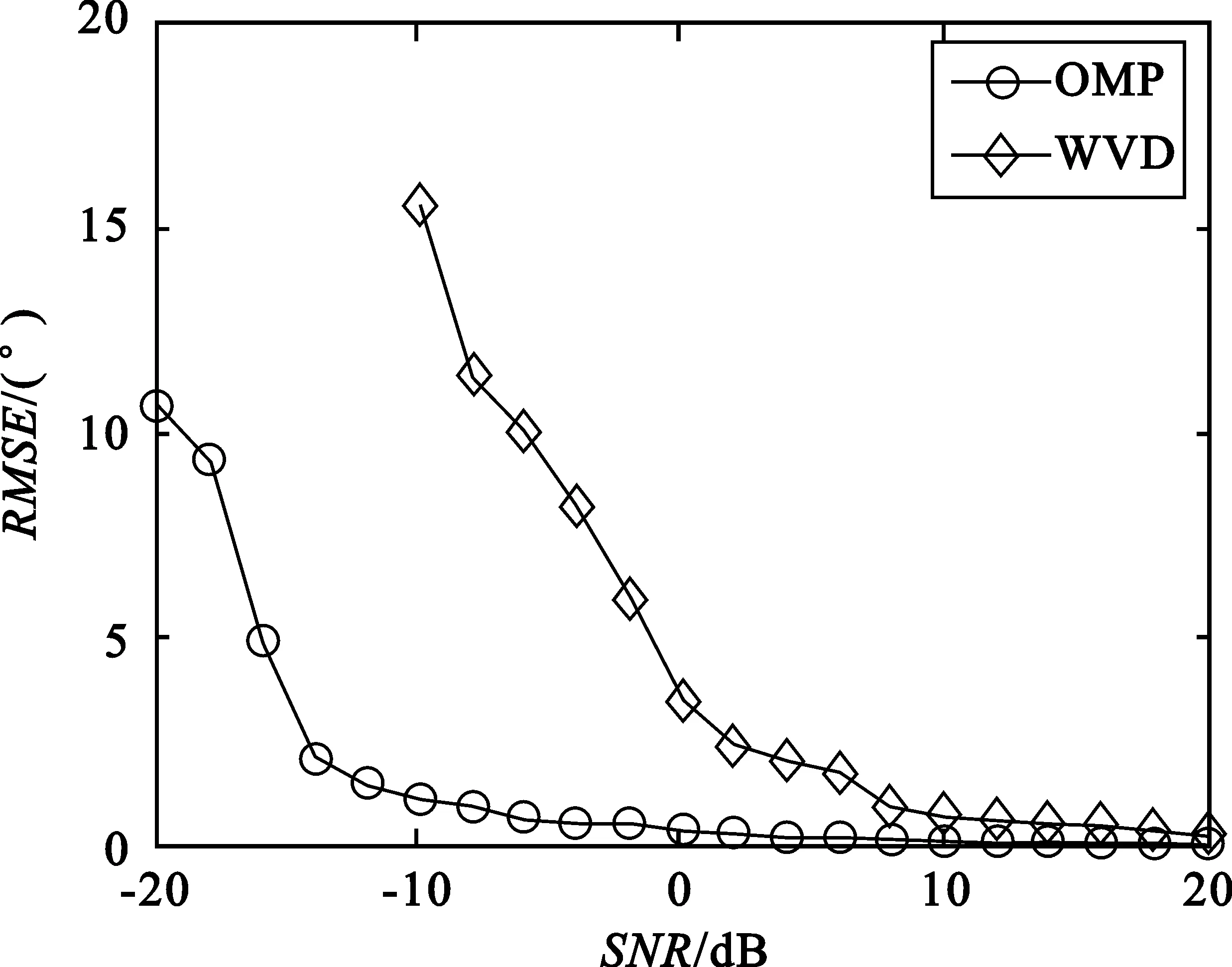
将此方程对0≤m (12) 式中,Pvk是在um0≤m 〈Rmx,um〉=〈Rmx,gγm〉 (13) 因Vk的维数为k,故存在M使得x∈VM,从而Rmx=0。将式(13)代入式(12),并令k=M,得: (14) 做有限M次迭代可以得到收敛性。它是x在一个正交向量族上的分解,故: (15) 此过程即为OMP的基本步骤,因为信号残差和前面每一步中从原子库中选择的原子相正交,在有限维空间中,OMP能在有限次迭代后收敛。 假设有P个宽带Chirp信号从不同方向入射到M元阵列上,则参考阵元接收数据为 (16) 对P个宽带Chirp信号进行离散化,得: (17) 式中,i=1,2,3,…,P;n=1,2,3,…,N;fs为采样频率。 根据宽带Chirp信号形式,建立过完备原子库,其基本原子为 (18) 原子gγ的长度与信号x1n本身长度相同,原子参数组为γ=f,k,f、k分别对应Chirp信号的起始频率和调频斜率参量。假设f的取值范围为f∈0,0.6,k的取值范围为k∈0,0.1,f、k按照需要的精度取值(本文设原子库的搜索精度为0.001),构造出过完备原子库Df=gγγ∈Γ: Df=gγγ∈Γ= (19) 式中,Γ为参数组γ所属的集合,其值视具体情况而定。 由于OMP分解的特性,对Chirp信号进行分解时,将在某一分量上达到最大匹配,而噪声不具有Chirp信号的特征,因此在这一分量上投影接近零,从而可以达到滤除噪声的目的。将淹没在噪声中的多个Chirp信号进行OMP分解,将会在不同分量上得到最大匹配,根据这些与信号最大匹配的原子参数,即可估计出每个Chirp信号的起始频率和调频斜率。 经过P步OMP分解后,可以得到P个原子gγi和原子系数αi=〈Ri-1xin,gγi〉。根据原子的参数γi=fi,ki就可以得到P个Chirp信号的起始频率和调频斜率参数估计: (20) (21) 由此,我们可以重新构造出P个宽带Chirp信号: (22) 在得到Chirp信号具体形式的基础上,我们再进行DOA估计。 首先,针对各个不同的Chirp信号分别建立过完备库的原子: (23) Gθgl=g1,g2,g3,…,gL (24) 整个原子库的原子数为L个。 通过在原子库Gθgl上对阵列信号用OMP算法做稀疏分解,由所获得的最佳原子便可以得到信源DOA估计参数,我们通过计算阵列接收数据与原子库Gθgl中原子之间的互相关矩阵的迹,搜索迹的最大峰值来获得。假定互相关矩阵Rxy的m个特征值为λ1,λ2,λ3,…,λm。由矩阵的迹的概念可知: (25) 即互相关矩阵Rxy的特征值之和trRxy反映了两信号xt和yt之间的相关程度。由此,分别计算阵列接收数据矩阵xn与原子库Gθgl中原子gl的互相关矩阵: (26) 并求解互相关矩阵Rxg的迹,通过比较迹的大小获得最佳匹配原子gi的参数,进一步得到DOA估计: (27) 综合上述分析,将基于OMP分解的宽带Chirp信号参数估计算法步骤总结如下: (1)建立过完备库的原子gγ,如式(18)所示,进一步建立过完备原子库Df=gγγ∈Γ,如式(19)所示; (3)建立过完备库的原子gl,如式(23)所示;进一步建立原子库Gθgl,如式(24)所示; (5)多信号时重复第3步和第4步,得到各个信号的DOA估计。 为体现OMP算法中信号原子之间的正交性,考虑5个宽带Chirp信号从远场入射到八阵元均匀线阵,信号的起始频率和调频斜率分别如下: 信号1:f10=0.150 000 1,K1=0.033 000 000 01; 信号2:f20=0.250 000 1,K2=0.066 000 000 01; 信号3:f30=0.350 000 1,K3=0.099 000 000 01; 信号4:f40=0.450 000 1,K4=0.055 000 000 01; 信号5:f50=0.550 000 1,K5=0.077 000 000 01。 5个信号的波达方向角分别为10°、20°、30°、40°、50°,阵元间距为信号最高频率对应的半波长。 (1)实验1:用OMP算法和WVD算法进行DOA估计的空间谱 (a)OMP的空间谱曲线 (b)WVD的空间谱曲线图1 五信源的DOA估计的空间谱Fig.1 Spatial spectrum curve of DOA estimation of five source signals 从图1中可见,OMP算法准确有效地估计出了5个信源的波达方向,在波达方向角为10°、20°、30°、40°、50°处,空间谱出现了谱峰,而WVD算法在40°处出现偏差。仿真结果表明,OMP算法的估计性能优于WVD算法。 (2)实验2:用OMP算法对宽带Chirp信号起始频率和调频斜率的估计 信号采样长度取N=512。用OMP算法估计信号1、信号2、信号3的起始频率和调频斜率。信噪比从-20~20 dB,每隔1 dB进行100次Monte-Carlo实验,实验结果如图2和图3所示。 (a)信号1 (b)信号2 (c)信号3图2 3个信号的起始频率估计Fig.2 The starting frequency estimation of three signals (a)信号1 (b)信号2 (c)信号3图3 3个信号的调频斜率估计Fig.3 Modulation frequency estimation of three signals 由图2和图3可见,OMP算法很好地实现了对Chirp信号起始频率和调频斜率的估计。在信噪比为-20 dB时,OMP算法对起始频率和调频斜率的估计性能很好,估计误差较小。3个信号的起始频率估计误差分别为0.11、0.15、0.14,调频斜率估计误差分别为0.03、0.03、0.053;在信噪比门限值-2 dB时,起始频率和调频斜率估计误差(RMSE)值达到了克拉美罗限,并且当信噪比进一步增加时,由于本文所设的原子库的搜索精度为0.001,OMP算法只能估计到起始频率和调频斜率真实数值的小数点后3位,且估计值不再随信噪比的增加而变化,故估计误差(RMSE)不随信噪比的增加而增加,在仿真结果中表现为一条水平的线段;当信噪比在信噪比门限值-2 dB以下时,OMP算法对起始频率和调频斜率的估计误差随信噪比的增加越来越小。 (3)实验3:用OMP算法和WVD算法对宽带Chirp信号的DOA的估计性能与快拍数的关系 (a)信号1 (b)信号2 (c)信号3图4 3个信号DOA估计的RMSEFig.4 RMSE of three signals DOA estimation 固定信噪比为10 dB,分别采用OMP算法和WVD算法,信号采样长度N(取值从100到1 000)每隔100进行200次Monte-Carlo仿真实验。图4给出了这两种算法在信噪比为10 dB时,在不同快拍数下的3个信号DOA估计的RMSE曲线。 从图4可见,在固定信噪比为10 dB条件下,随着信号采样长度的增加,OMP算法的DOA估计的均方误差减小,且估计性能明显优于WVD方法。 (4)实验4:用OMP算法和WVD算法对宽带Chirp信号的DOA估计性能与信噪比的关系 实验中分别采用OMP算法(信噪比从-20~20 dB)和WVD算法(信噪比从-10~20 dB),信噪比每隔2 dB进行200次的Monte-Carlo实验。其中,阵元数M=8,信号采样长度N=512。结果如图5所示。 (a)信号1 (b)信号2 (c)信号3图5 3个信号DOA估计的RMSEFig.5 RMSE of three signals DOA estimation 由图5明显可见,OMP算法对信号DOA估计效果非常好。随着信噪比的提高,DOA估计的均方误差越来越小,估计精度明显优于WVD方法。在信噪比为-14 dB时,该算法仍具有很好的性能,而WVD方法在-10 dB几乎失效。 本文通过大量的仿真实验证明了在多信源低信噪比的情况下,OMP对宽带阵列信号参数估计的有效性。论文的研究尤其在以下方面得到了很大改进:在信噪比为-20 dB时,OMP算法对起始频率和调频斜率的估计性能仍很好;在信噪比门限值为-2 dB时,该方法对起始频率和调频斜率的估计的RMSE值达到了克拉美罗限;在信噪比为-14 dB时,该方法对波达方向角度的估计仍然有良好的性能,且其估计精度明显优于传统的WVD方法。 参考文献: [1] 张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社,1998. ZHANG Xian-da, BAO Zheng.Non-stationary signal analysis and process[M].Beijing:National Defense Industry Press, 1998.(in Chinese) [2] Belouchrani A, Amin M G. Blind source separation based on time-frequency signal representations [J]. IEEE Transactions on Signal Processing, 1998,46(11):2888-2897. [3] Belouchrani A, Amin M G. Time-frequency MUSIC [J].IEEE Signal Processing Letters,1999, 6(5):109-110. [4] Schmidt R O. Multiple emitter location and signal parameter estimation [J].IEEE Transactions on Antennas and Propagation, 1986,34(3):276-280. [5] Roy R,Kailath T.ESPRIT-estimation of signal parameters via rotational invariance technique[J].IEEE Transactions on Acoust, Speech and Signal Processing,1989,37(7):984-995. [6] Mallat S,Zhang Z. Matching Pursuit with Time-frequency Dictionaries[J].IEEE Transactions on Signal Processing, 1993, 41(12):3397-3415. [7] 杨愚.图像稀疏分解快速实现与初步应用[D].成都:西南交通大学出版社,2007. YANG Yu.Fast implement and preliminary application of picture sparse decomposition[D].Chengdu: Southwest Jiaotong University Press, 2007. (in Chinese) [8] 张贤达.现代信号处理[M].北京:清华大学出版社,2002. ZHANG Xian-da.Modern Signal Processing [M].Beijing:Tsinghua University Press, 2002. (in Chinese)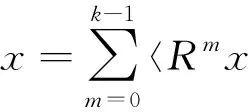
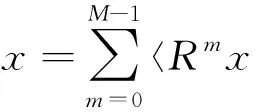
3.1 宽带Chirp信号起始频率和调频斜率的估计
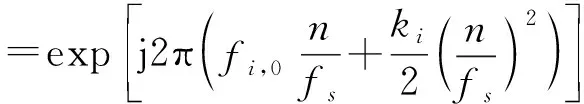
3.2 宽带Chirp信号的DOA估计
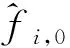

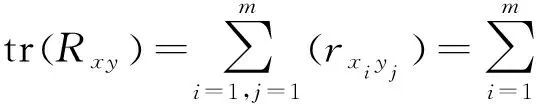
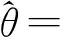
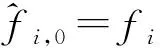
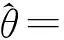
4 仿真实验




5 结 论

