利用有向图实现多用户下行多天线系统的用户选择
(1.海军航空工程学院 青岛分院,山东 青岛 266041;2.海军飞行学院,辽宁 葫芦岛 125001)
1 引 言
在多用户下行多天线系统中,基站可通过同时将独立的数据流发送到多个用户来保证高的和速率,其技术难点在于如何设计发射向量以消除用户间的共信道干扰。DPC编码在理论上被证明可获得与在无干扰环境下相同的信道容量[1],但因为基于DPC编码的算法需要基站已知所有同时工作的用户附加噪声的干扰信息,其高度非线性、极高的复杂度以及和现有通信编码方式的不兼容性使其很难实用。迫零波束成形算法是一个次优的算法,当用户数趋于无穷的时候它可以达到和DPC算法同样的和容量[2]。在高信噪比情况下,采用Tomlinson-Harashim预编码(THP)[3]能够达到下行多用户多天线系统的和容量。以上预编码技术都需要发端实时知道每个用户的信道状态信息,这在实际的系统中很难实现。特别是在FDD系统中,为了使发送端得到及时、准确的接收端信道信息,接收端必须不断地通过多址接入信道将自己的信道状态信息反馈到发送端,巨大的反馈数据量降低了系统的效率,同时,反馈造成了发送端的信息滞后于实际的信道变化,也会对系统性能造成一定影响。因此,研究在发端已知部分信道状态信息下的预编码技术尤其重要。文献[4] 根据Grassmann流形码本[5]提出了一种有限反馈的多用户下行多用户多天线系统的发送策略,其基本思想是先通过用户选择,根据有限的信道反馈量选择互相之间干扰最小的用户一起工作以获得最大的系统和速率。该算法克服了常规的随机波束成形算法[6]只有在用户数非常多的时候才能有效工作的弱点,因此更具有实用性。本文在文献[4]的基础上提出了一种基于有向图的用户选择算法,可以大大加快用户选择的速度, 在用户数少或中等的时候能得到比常规的随机波束成形算法更好的性能。
2 系统模型
考虑一个多用户下行系统,基站端有nT根发送天线,系统中的总用户数为K,每个用户有ni根天线,i=1,2,3,…,K。每个用户的信道假设为准静态和平衰落,可以表示为ni×nT维矩阵Hi。每个用户在接收端已知自己的信道矩阵但基站端未知。假设S是发送信号矢量且E{S*S}=nT,也就是总发送功率是nT。基站在所有被选择的用户中平均分配功率,用户i接收到的信号可以表示为
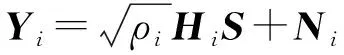
(1)
式中,Yi是ni×1维接收信号矢量,Ni是ni×1维加性噪声,各元素为服从独立同分布、均值为0、方差为1的复高斯随机变量。为了便于和常规的随机波束成形算法进行比较,类似文献[6],先假定所有用户ni=1,各用户具有相同的SNR即ρi=ρ(i=1,2,3,…,K)。随机波束成形算法中是随机产生nT维独立分布的正交矢量作为nT个用户的发射矢量,而在我们的算法中先从基于Grassmann流形构造的码本C=C1,C2,…CP中选择nT维矢量φm(m=1,2,3,…,M)。M是同时工作的用户数目,根据用户信道的状态信息以及用户信道间的空间相互关系确定,M不大于nT,M的确定将在后面的用户选择算法中详细讨论。码本是离线确定的,基站和每个用户已知。基站的发送信号为
(2)
式中,sm是第m个用户的发送符号。根据假设,发送总功率为nT,每个用户的发送功率是E{si2}=nT/M,则第i个用户的接收信号为
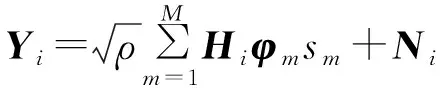
(3)
3 用户选择算法
由于Grassmann流形码本的构造和发射波束的选择准则是针对单用户环境的,并没有考虑用户之间的干扰,不能直接应用。在多用户环境中,除了在选择发送波束的时候,要使发射波束和用户信道匹配之外,一个重要的问题是还要使用户之间的干扰最小。为解决这个问题,可以通过合理的用户选择使信道正交性最好的用户一起工作,这样可以使一个多用户信道近似分解为若干平行独立的单用户信道。那么,在单用户环境中设计的码本和选择准则就能应用了。尽管通过用户选择后还会存在一定的干扰,可以通过增加用户数获得多用户分集增益的方法来解决。
根据系统模型,用户i的输出SINR为
(4)
系统的瞬时和速率为
(5)
在多用户环境中,每个用户不仅需要反馈表示其本身信道增益的信息,还要反馈其对其它用户的干扰信息,根据这些信息我们可以选择互相之间正交性用户一起工作,使用户之间干扰最小。用户选择的准则实际上就是最大化式(5)的和速率。第i个用户在码本中选择最适合它的发送矢量φi和分配给其它用户的能使它的SINR最大化的(nT-1)个矢量。定义Ai为(nU-1)个矢量的标号,di定义为φi的标号。位于di中的发射矢量是和用户i的信道最匹配的,位于Ai的发射矢量是对用户i干扰最小的发射矢量。
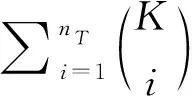
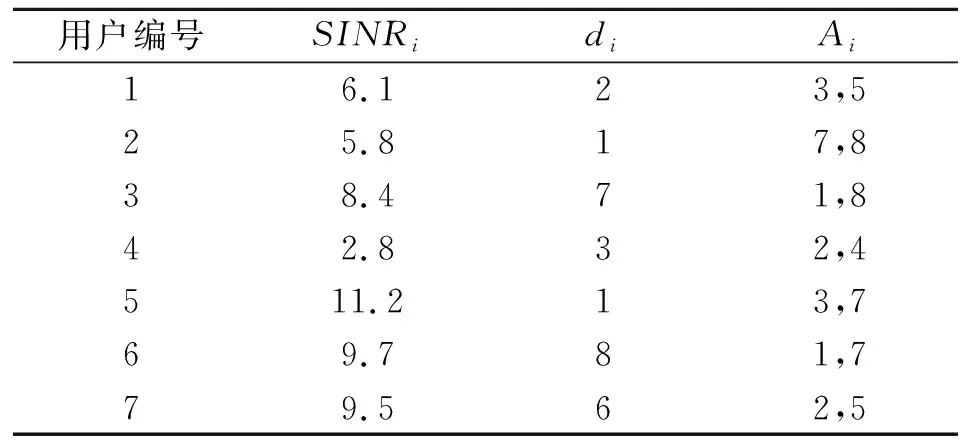
表1 所有用户反馈的信道状态信息(K=7)Table 1 Feedback channel state information of all users(K=7)
首先根据表1用户反馈的信道状态信息构造有向图,如图1所示。每一个用户生成一个顶点,其中顶点旁小方框里的数字表示用户编号,顶点圆圈里的数字表示该用户的di。各用户根据其Ai中的数值向和它有相同数值的其它用户的顶点di画出有向边。这里说明一下,如果某一用户Ai中的某一数值没有任何用户的顶点di和它相同,则不画有向边。如果某一用户Ai中的某一数值和多个用户的顶点di相同(不同用户可以有相同的di)则画出多条有向边。为了使例子更具有一般性,表1中的用户2和用户5就是具有相同的di={1},当然它们的Ai不相同,如果Ai完全相同,则这两个用户可以合并成一个,只需要考虑SINRi大的用户即可。用户3的Ai中有元素1,所以它需要分别向用户2和用户5画两条有向边。按照以上准则构造好有向图,用户选择的问题就变成了在图中寻找闭合环的问题。例如,如果图中用户1和用户4要一起工作,A1中要包含d4,A4中要要包含d1,形成图1中的单向环。也就是说,和用户1的信道最匹配的发送矢量恰好是对用户4干扰最小的矢量,而和用户4的信道最匹配的矢量恰好是对用户1干扰最小的。对于有3个用户一起工作的情况要复杂一点,将形成图1中用户2、用户3和用户6所形成的双向环。对用户2干扰最小的发射矢量恰好是和用户7和用户8信道最匹配的矢量,对用户3和用户6也是类似的关系。为了更好从有向图中搜索到闭合环,这里先介绍一下图论里的两个基本术语[7]:入度和出度。在有向图中则以某顶点为终点的有向边数目称为该顶点的入度,从某顶点出发的有向边的数目称为该顶点的出度。利用有向图中各顶点的入度和出度可以判断环的存在。如图中可同时工作用户1和用户4的顶点的入度和出度至少都大于等于1,可同时工作的用户2、用户3和用户6的顶点的入度和出度都至少要大于等于2。一般地,如果有n个用户可以同时工作,则各用户对应的顶点的入度和出度都需要大于等于n-1。 按照这个原则,在判断系统能否同时支持nT到1个用户的过程中可以依次排除不满足条件的用户。
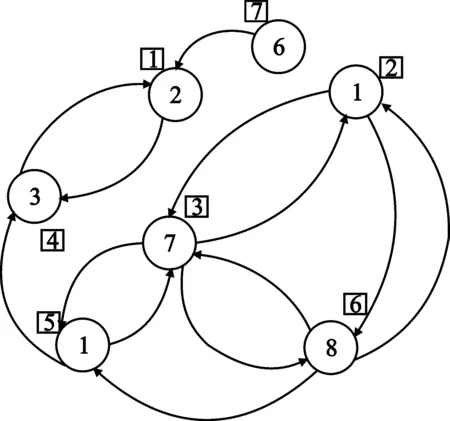
图1 有向图的构造Fig.1 Construction of directed graph
由于nT=3,我们首先检查是否存在满足3个用户同时存在的环。去掉所有不满足入度和出度都大于等于2这个条件的顶点及其相应的边。如图2所示,图中去掉的顶点与相应的边用虚线表示(下同)。再次检查各顶点的入度和出度,用户5的顶点在去掉和用户4相连的边后也不满足入度和出度都大于等于2这个条件了,去掉用户5的顶点及相应的边,如图3所示。这样,满足条件的只剩下用户2、用户3和用户6的顶点了。按照避免SINRi的中断条件进一步检查,集合{2,3,6}是可以一起工作的一组用户了。如图4所示,由于集合{2,3,6}的子集的和速率一定小于其父集合的和速率,所以在进行进一步的用户搜索之前要去掉构成集合{2,3,6}一起工作的相应的边。如果某一用户顶点的所有的边都去掉了,则顶点本身也去掉(如用户2的顶点)。第二步检查是否存在满足2个用户同时工作的环。去掉所有不满足入度和出度都大于等于1这个条件的顶点及其相应的边。在这一步,如图5,去掉用户6和用户7的顶点,及相应的边。再剩下的用户的顶点中按照避免SINRi的中断条件进一步检查,用户集合{1,4}和{3,5}可以同时工作。最后一步确认单独工作的用户,选择没有组成任何环路的用户。只需从全部用户的集合中去掉前两步中已选择过的用户集合即可。
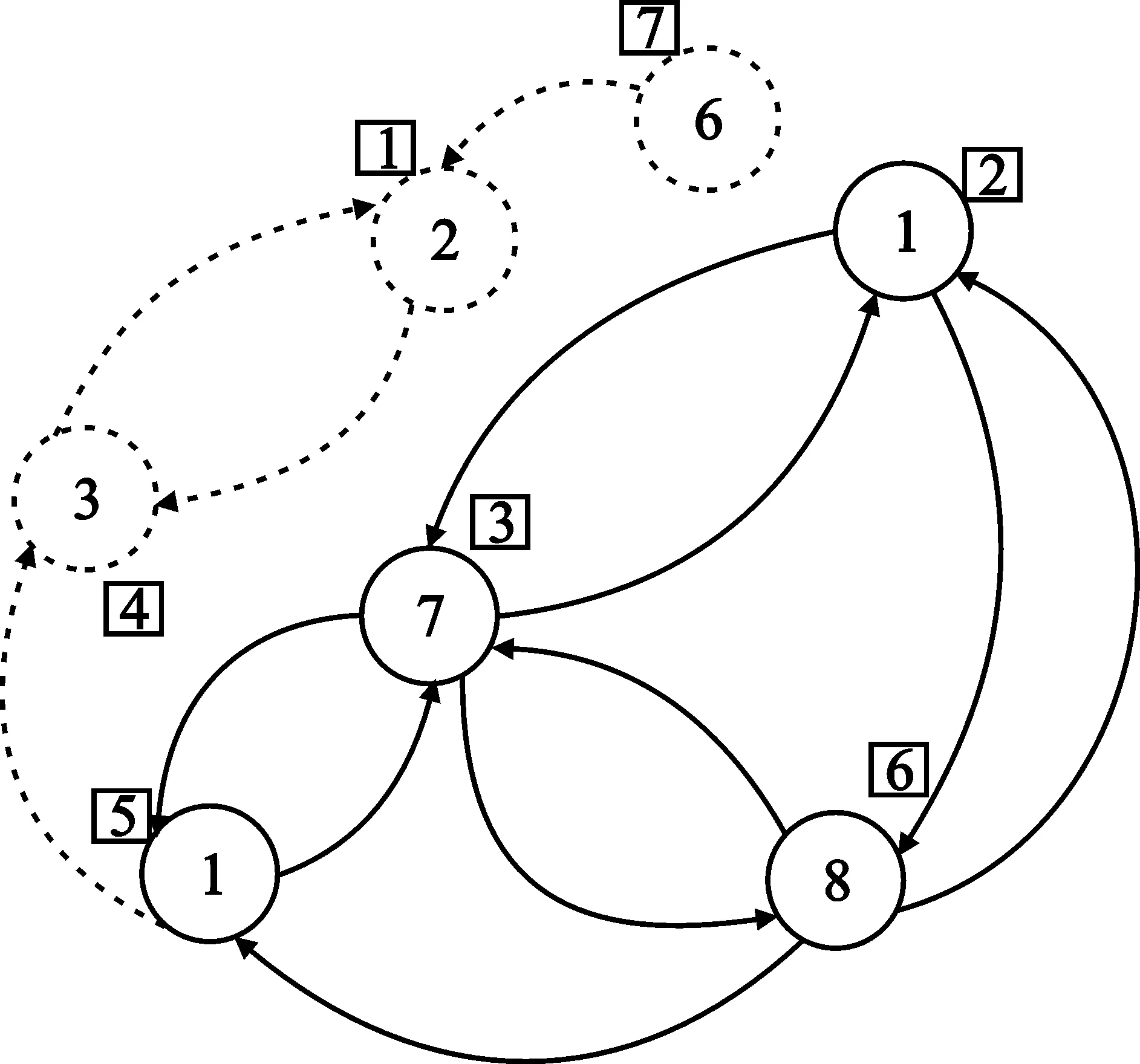
图2 有向图用户搜索(1)Fig.2 No.1 directed graph based user selection
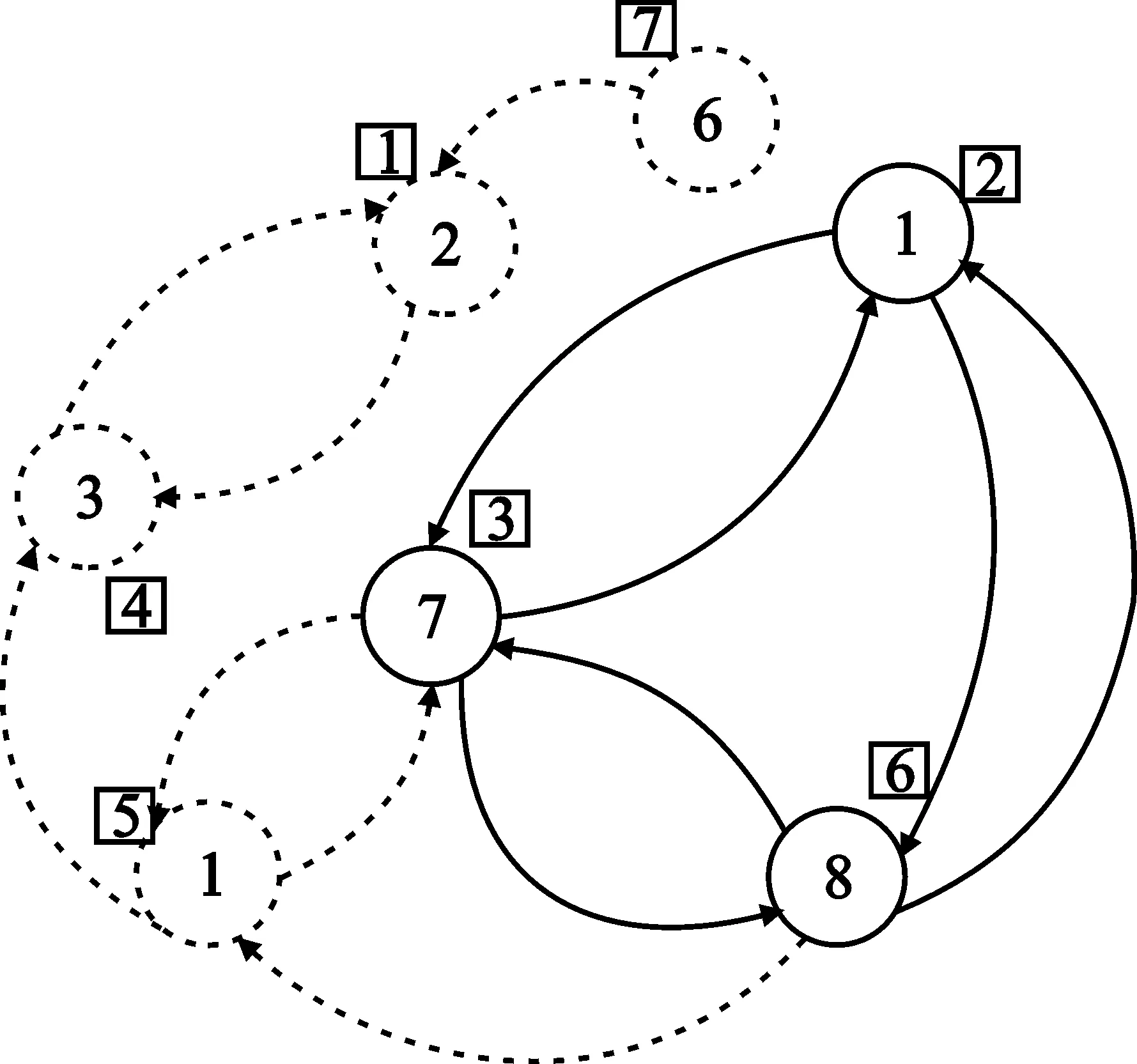
图3 有向图用户搜索(2)Fig.3 No.2 directed graph based user selection
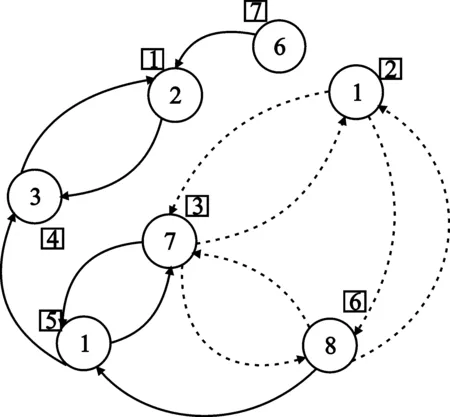
图4 有向图用户搜索(3)Fig.4 No.3 directed graph based user selection
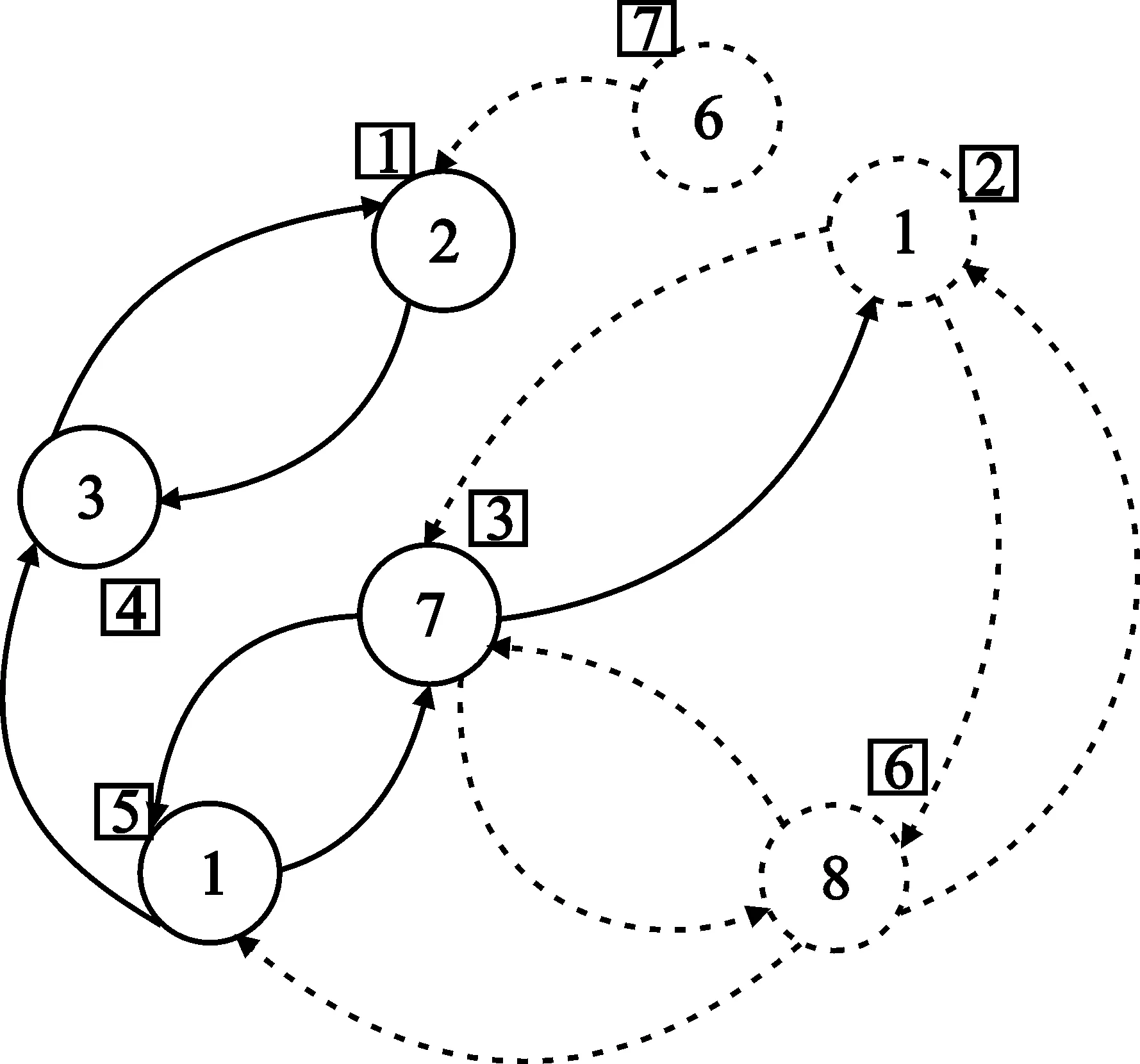
图5 有向图用户搜索(4)Fig.5 No.4 directed graph based user selection
根据以上用户选择算法,基站只需要考虑以下可能的用户集合:{2,3,6},{1,4},{3,5},{7}。根据式(5)计算所有可能的用户集合,最后选择能使和速率最大的集合{2,3,6},也就是说同时工作的用户数是3。如果集合{3,5}或{7}比集合{2,3,6}有更大的和速率,则同时工作的用户数是2或1。同时工作的用户数是根据各用户之间的信道状况和反馈的信息自适应调整的。
根据前面的例子,可以归纳用户选择算法如下:
步骤1:所有的用户反馈其SINRi、di和Ai给基站,Θ=1,2,3,…,K,i∈Θ,j=nT;
步骤2:采用前述基于有向图的用户选择算法从集合Θ中选择可以使j个用户同时工作的所有可能的子集Sj,k,k=1,2,3,…,Nj(Nj是子集的数目);
步骤3:对任意k∈{1,2,3,…,Nj},Θ=Θ/Sj,k;
步骤4:j=j-1;
步骤5:重复步骤2~5直到j=1或Θ为空集;
步骤6:用公式(5)计算所有可能子集Sj,k(j=1,2,3,…,nT;k=1,2,3,…,Nj)的和速率,选择其中和速率最大的子集为最终选择的用户集合。
4 仿真结果与分析
通过计算机仿真将文中提出的基于Grassmann流形码本的多用户下行多用户多天线系统的发送算法和经典的多波束随机波束成形算法做了比较。信道假定为准静态瑞利平衰落,系统有一个基站,基站有nT=3根天线,每个用户有ni=1根天线。
图6和图7分别为发送算法在不同码本大小和不同用户数情况下的和速率。每个用户的SNR分别为ρ=0 dB和ρ=20 dB。作为对照,文献[6]中随机波束成形的算法的结果也表示在图中。通过仿真结果可以看出,选择合适的码本维数大小,本文所提出的发送算法在用户数少或中等的时候能得到比随机波束成形算法更好的性能。码本维数越大效果越好,但需要更多的反馈量。码本的维数越大,基站就越容易选择到空间关系正交性好的用户,从而得到更大的和容量。从图6和图7还可以看出,在高信噪比时,基于Grassmann流形码本的发送算法比常规多波束随机波束成形算法有更大的性能增益,这可以解释为在高信噪比时系统是干扰受限的,用户之间的干扰对性能影响最大;而基于Grassmann流形码本的发送算法由于选择更大的码本维数,所以在用户选择的时候具有更大的空间自由度,更容易选择到匹配的发送矢量,使得用户之间的干扰最小。
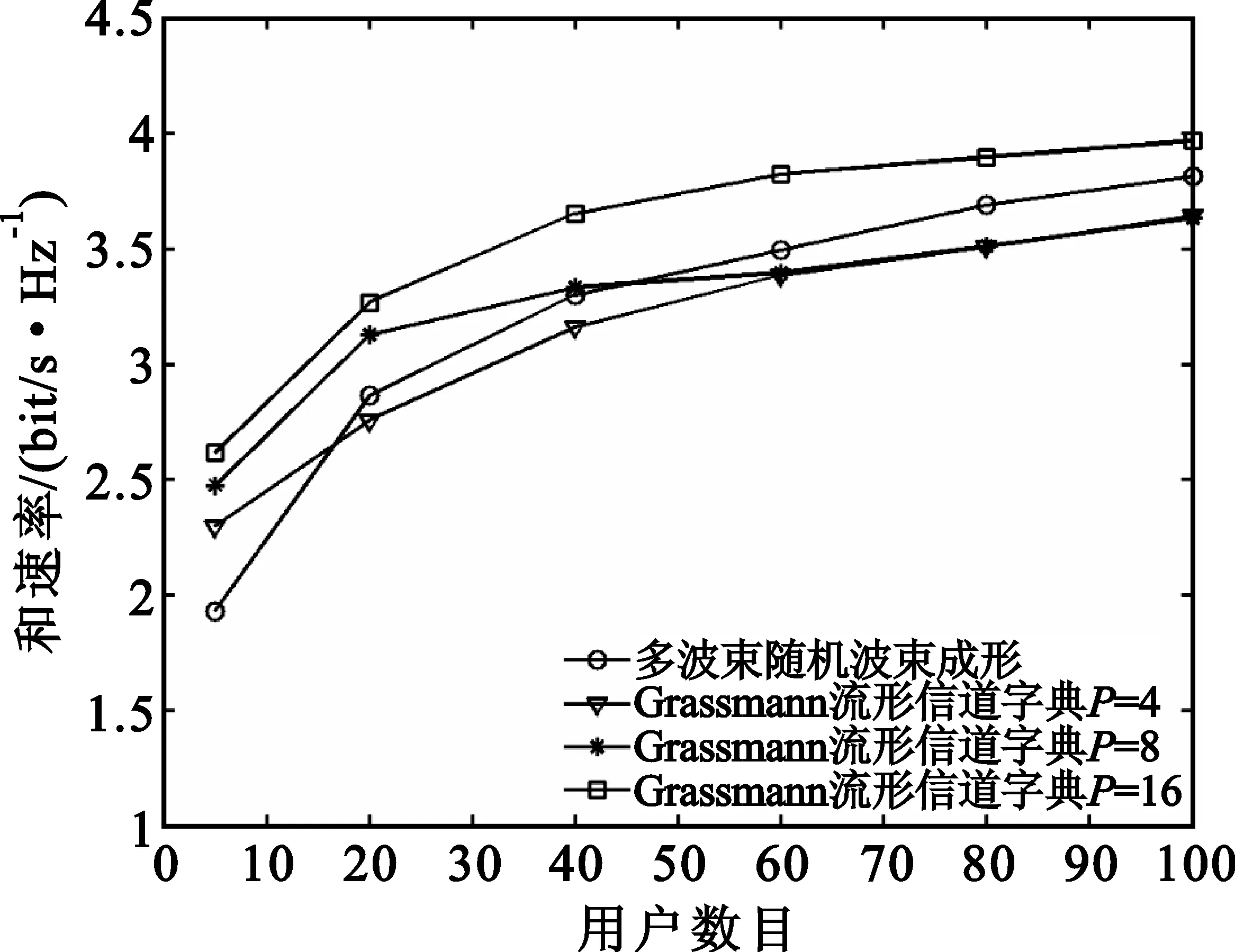
图6 不同用户数目下的和速率(SNR=0 dB)Fig.6 Sum rate throughput versus the number of users when SNR=0 dB

图7 不同用户数目下的和速率(SNR=20 dB)Fig.7 Sum rate throughput versus the number of users when SNR=20 dB
5 结 论
在多用户下行多天线系统中,由于基站很难实时得到各用户的完全信道状态信息,研究在发端已知部分信道状态信息下的预编码技术尤其重要。根据有限的信道反馈量选择互相之间干扰最小的用户一起工作可以获得最大的系统和速率。本文提出的利用有向图实现多用户下行多天线系统的用户选择方法,实质上是将用户选择的问题变成了在有向图中寻找闭合环的问题,大大降低了用户选择算法的复杂度。通过计算机仿真证实了该算法克服了常规随机波束成形算法只有在用户数非常多的时候才能有效工作的弱点,在用户数少或中等的时候能得到比其更好的性能,而这恰好适应实际系统中每一个基站同时服务的用户较少的情况,因此更具适用性。本文介绍的用户选择算法的系统模型是以码本法为基础的,而采用码本法减轻信道反馈量实际上是对用户瞬时信道状态信息进行量化,还可以进一步研究发送端只知道用户信道统计信息情况下的传输技术。
参考文献:
[1] CAIRE G,SHAMAI S. On the achievable throughput of a multiantenna Gaussian broadcast channel [J]. IEEE Transactions on Information Theory, 2003, 49(7): 1691-1706.
[2] DIMIC G,SIDROPOULOS N D. Low-complexity downlink beamforming for maximum sum capacity [C]//Proceeding of IEEE International Conference on Acoustics, Speech, and Signal Processing.Montreal, Quebec, Canada:IEEE,2004:701-704.
[3] WINDPASSINGER C, FISCHER R F H, VENCELT, et al. Precoding in multiantenna and multiuser communications [J]. IEEE Transactions on Communications,2004,3(4):1305-1316.
[4] ZHENG Hai-bo, WU Yong-le, LI Yun-zhou, et al. Limited Feedback Precoding Scheme for Downlink Multiuser MIMO Systems [J]. IEICE Transactions on Communications, 2007, E90-B (3): 689-692.
[5] LOVE D J, HEATH R W,STROHMER T. Grassmannian beamforming for multiple-input multiple-output wireless systems [J]. IEEE Transactions on Information Theory,2003, 49(10): 2735-2747.
[6] SHARIF M,HASSIBI B. On the capacity of MIMO broadcast channels with partial side information [J]. IEEE Transactions on Information Theory, 2005, 51 (2): 506-522.
[7] BONDY J A,MURTY U S R. Graph Theory with Applications [M]. New York: Macmillan Ltd. Press, 1976.

