基于BP神经网络的直扩信号扩频码盲识别
(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)
1 引 言
虽然扩频通信最初是为军事应用而开发的,但是现在已被广泛用于商业应用,特别是码分多址(CDMA)通信,或全球定位系统(GPS)。扩频技术由于其本身具备的优良性能而得到广泛应用,到目前为止,其最主要的两个应用领域仍是军事抗干扰通信和民用无线通信系统。一般而言,跳频系统与直扩系统则分别是在这两个领域应用最多的扩频方式,它们具有完全不同的抗干扰机理,前者采取的是“躲避”策略,即载有信息的载频在某一频率集内随机跳变,使非合作方无法进行跟踪干扰;后者则采用的是“隐蔽”策略,即通过扩频把直扩信号的功率谱密度降低,直至被噪声所淹没,使非合作方无法检测并截获到有用直扩信号。扩频通信中通常接收方必须要知道发送方使用的扩频序列才能用相关器解扩恢复所传输的数据。
我们的目的是自动确定扩频序列,而接收方此时并不知道发送方的伪噪声(PN)码。文献[1]提出了基于分段互相关的PN码序列快速盲估计,但是该盲估计还是要先搜索信息码波形与PN码波形同步起始点,且在伪码很长时计算开销比较大。文献[2]使用了带约束的Hebb学习规则来对DS信号PN码进行估计,但其是在已知信息码波形与PN波形同步起止时刻的前提下来进行估计的。文献[3]使用统计谱分析结合神经网络的方法实现对DS信号PN码序列的估计,但是该文提到了用来搜索信息码波形与PN码波形同步起始点的自相关方法存在较为严重的缺陷,因此在实用上增加了DS通信盲解扩处理的难度。文献[4]提出了一种主分量神经网络(N.N.或Neural Networks)的解决方法,该方法充分利用了无监督N.N.的自适应主分量提取特性,能较好完成直扩信号伪码序列的盲估计。
本文提出一种不同于文献[4]的方法,其最主要的区别在于该方法是基于有监督的反向传播(BP)神经网络,而文献[4]是基于无监督的主分量神经网络。本文的方法仅需知道符号周期即可,因而克服了文献[1-3]所提方法的缺陷。
本文首先简要介绍直接序列扩频(DSSS)技术,解释在非合作通信中恢复数据的难度;然后,介绍利用BP神经网络来解决问题的方法;最后,第4部分给出在不同的信号情况下的实验结果。
2 DSSS技术
直接序列扩频所传送的信息符号经伪随机序列(或称伪噪声码)扩频后对载波进行调制。伪随机序列的速率远大于要传送信息的速率,因而调制后的信号频谱宽度将远大于所传送信息的频谱宽度。
2.1 简化的直扩信号发送接收模型
假设信息信号为
(1)
式中,an=±1为等概分布的信息码序列,q(t)是持续时间为Ts的矩形脉冲。
假设PN序列的周期长度为P,定义PN序列为y,即:
y=y0,y1,y2,…,yP-1
(2)
(3)
假设接收方知道扩频序列,可以用一个相关器来解扩信号,解扩方法如下:
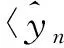
(4)
根据PN序列的性质,可以恢复出信息码。
然而,当接收方不知道发送方使用的扩频码序列时,则恢复信息码将变得极具挑战性。

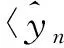
(5)
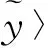
2.2 实际使用的DSSS系统模型
通常情况下,直接序列扩频系统使用二进制或四进制相移键控(BPSK或QPSK)数据调制。通常PN序列是最大长度的二进制m序列或Gold序列。
这里我们考虑一个BPSK数字调制,用一个特征伪码序列来对信号扩频。在接收滤波器输出端的基带接收信号可以写为
(6)
式中,h(t)是信道的联合冲激响应及扩频码,即:
(7)
p(t)=(e*g*c)(t)
(8)
式中,P是扩频序列的周期长度,{ym;m=0,1,2,…,P-1}是扩频序列,ak是第k个信息码符号,Tc是切普周期,Ts是信息码符号周期(Ts=PTc),e(t)是发送滤波器,c(t)是信道滤波器,g(t)是接收滤波器,p(t)是发射滤波器、信道冲激响应、接收滤波器的卷积,n(t)是接收滤波器输出端的噪声。基带信道噪声假设是均值为零的高斯白噪声。
本文中提出一种基于BP神经网络的方法来实现估计PN序列,该方法仅需知道信息码符号周期即可。
3 PN序列的盲估计
在不知道发送方PN序列的前提下,为了恢复数据信息,必须估计出h(t)。本节将用基于人工神经网络的方法估计PN序列。
3.1 理论分析
传输的信号如前所定义的一样。假设已知符号周期Ts,它可以用循环平稳分析来估计得到。接收信号的采样周期假设为Te,且Te=Tc,即一个切普采一个点,则有Ts=PTe。先以Te为采样周期对接收到的信号进行采样,然后将采样后的信号按Ts进行连续周期分段形成数据向量集。信号采样随机起始点记为t=mTs+t0,其中m为整数,0≤t0≤Ts。则接收信号x(t)按Ts进行连续周期分段所形成的数据向量为
xl=sl+nl,l=1,2,3,…
(9)
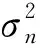
x(t)=x(t),x(t+Te),…,x(t+Ts-Te)T
(10)
同理,h(t)和n(t)以同样的方式定义。
我们可以根据采样后的信号按Ts进行连续周期分段后形成的数据向量集来创建一个P行N列的矩阵X,每一列为一周期的数据向量,N是用于估计的时间窗口数,即输入的数据组数。矩阵X如下所示:
(11)
从式(6)可以写出:
(12)
(13)
定义hk(t0)向量如下:
hk(t0)=h(t0+kTs),…,h(t0+(k+1)Ts-Te)T
(14)
因此有:
(15)
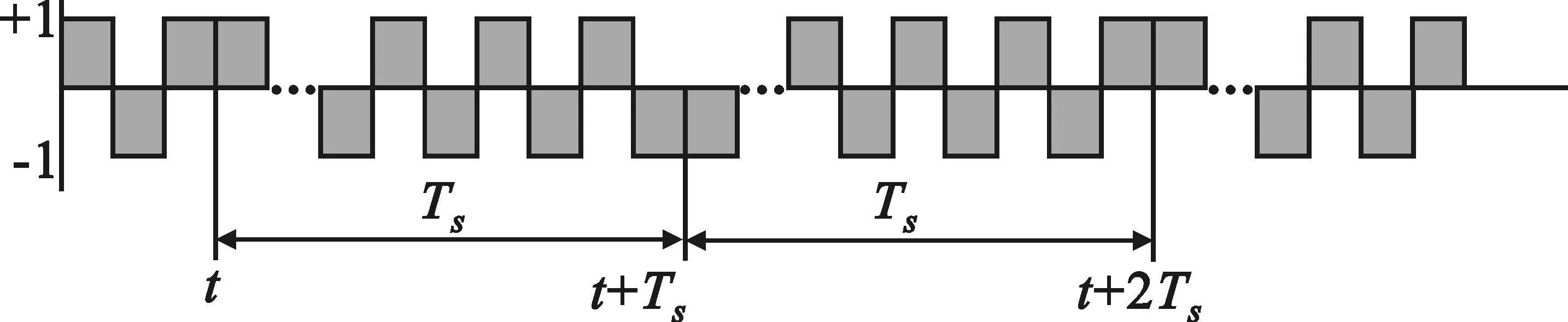
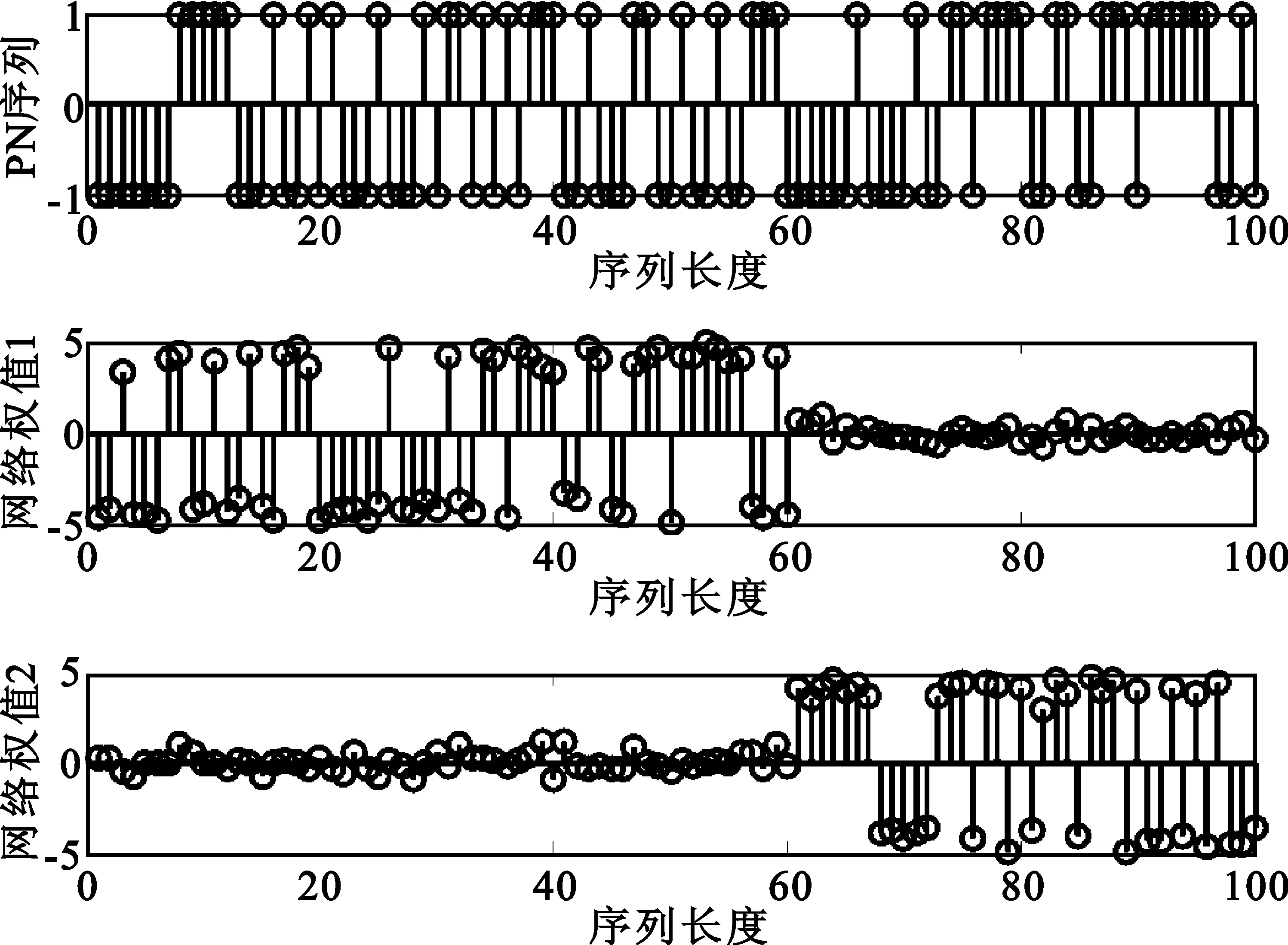
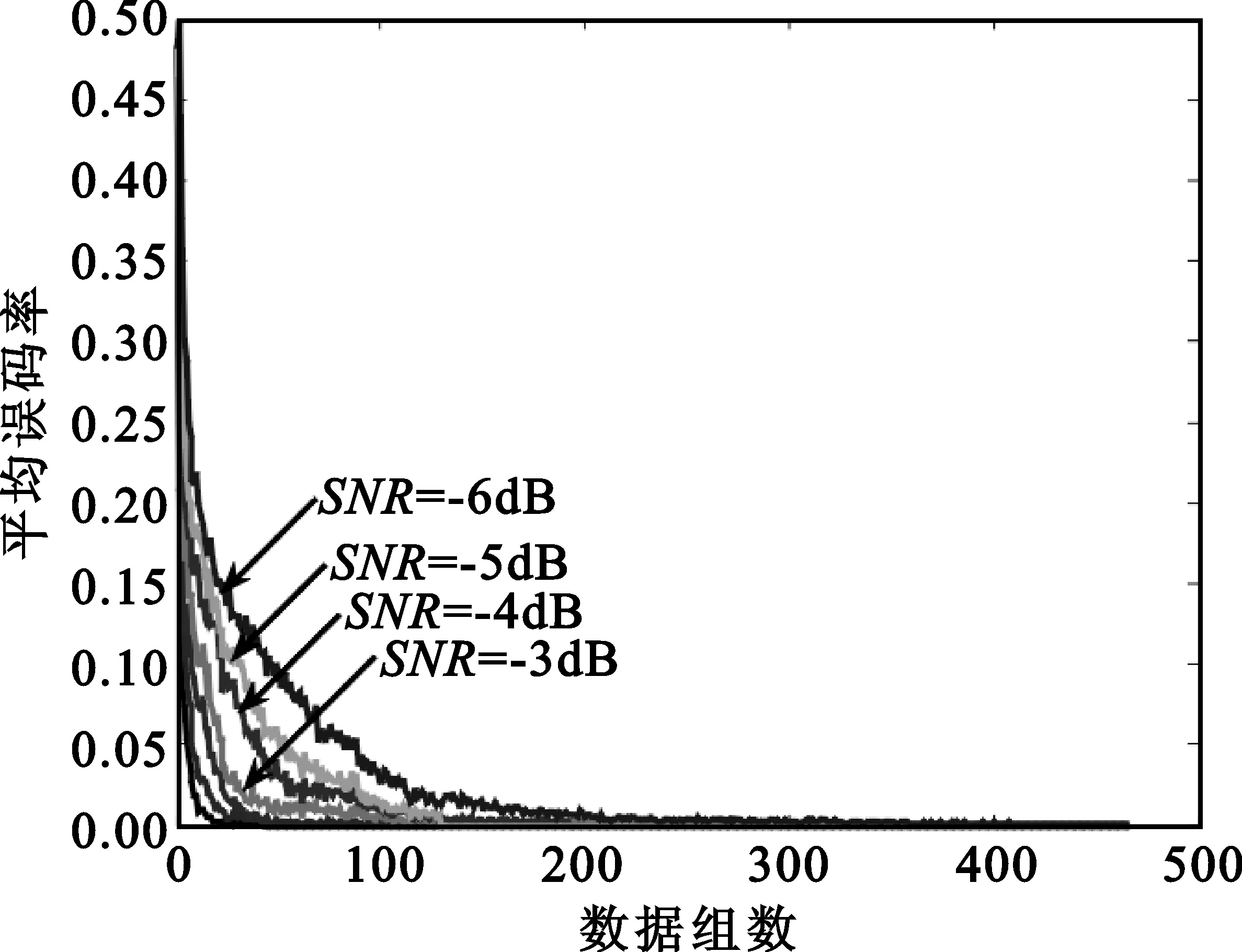
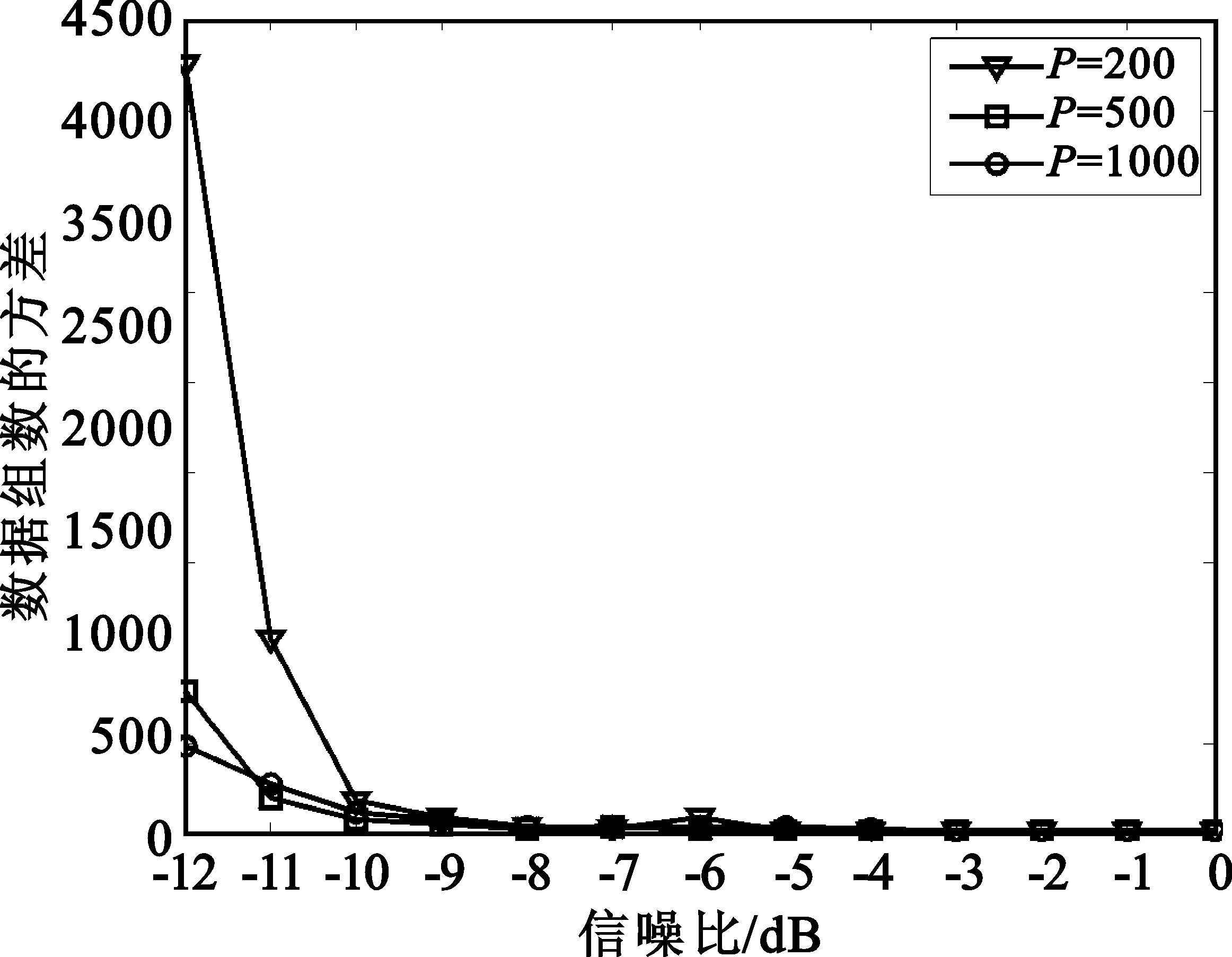
如果采样起始点t=mTs+t0并不恰好处于信息码与PN序列调制的同步点上(t0≠0,0 x(t)=amh0(t0)+am+1h-1(t0)+n(t) (16) 式中,h0(t0)是P维向量,该向量包含持续时间为Ts-t0的扩频波形的后半段,后面紧接着是持续时间为t0的零值,即: h0(t0)=h(t0),h(t0+Te),…,h(Ts-Te),0,…,0T (17) h-1(t0)也是P维向量,该向量包含持续时间为Ts-t0的零值,后面紧接着是持续时间为t0的扩频波形的前半段,即: h-1(t0)=0,…,0,h(0),h(Te),…,h(t0-Te)T (18) 因此我们可将矩阵写成如下形式: (19) 式中,am=am,am+1,…,am+N-1T,h0(t0)和h-1(t0)是正交的,噪声和信号是不相关的。因此由h0(t0)和h-1(t0)张成的子空间可以由3层神经网络来确定,该网络的隐层包含两个神经元[5]。事实上,估计的h(t)在第二层的权值上显示出来。 图1为简单的接收信号数据模型(未含噪声)。图1(a)是连续的信息码am,符号周期为Ts;图1(b)是扩频序列,切普周期是Tc;图1(c)是经过扩频以后的信号。输入信号数据为图1(c)中经采样后连续截取一周期的信号数据,如图所示,t到t+Ts之间的信号数据,t+Ts到t+2Ts之间的信号数据,依此类推。 (a)连续的信息码 (b)扩频系列 (c)扩频以后的信号图1 输入信号数据模型Fig.1 Model of input data 在此创建一个3层网络:一个输入层,一个含有两个神经元的隐层和一个输出层。 多层网络可以解决非线性可分问题,但是加入隐层使得学习比较困难,因此限制了多层网络的发展,反向传播(BP)算法的出现解决了这一困难。 本文用到的BP神经网络模型如图2所示。 图2 BP神经网络模型Fig.2 Model of BP neural network 该神经网络的输入数据向量x(n)是矩阵X的列向量,期望输出向量d(n)是和输入数据向量一样的数据向量,即d(n)=x(n)。根据BP算法来调节网络权值,该算法使得网络输出和期望输出的均方误差最小。 该神经网络有两种信号流通:一种是工作信号,它是施加输入信号后向前传播直到在输出端产生实际输出的信号,是输入和权值的函数;另一种是误差信号,即网络实际输出与期望输出之间的差值,它由输出端开始逐层向后传播。 设在第n次迭代中输出端的第k个神经元的输出为ok(n),期望输出为dk(n),则该神经元的误差信号ek(n)为 ek(n)=dk(n)-ok(n) (20) (21) 设最大迭代次数为N,则平方误差的均值EAV为 (22) 按照BP算法来运行网络,可以使均方误差达到最小[6]。 假设输入数据向量为矩阵X的列向量,可简化表示为 x(n)=x1(n),x2(n),…,xi(n),…,xP(n)T (23) 对于隐层的神经元有: (24) 典型的神经元激活函数为单极性sigmoid函数,所以隐层神经元的输出为 (25) 且有: yj(n)1-yj(n) (26) 对于输出层的神经元,有: (27) 计算输出层神经元的输出为 (28) 且有: ok(n)1-ok(n) (29) 然后反向计算各神经元的偏量值(误差对权值的梯度)δ。对于输出神经元,计算输出层的权值偏量值: ek(n)ok(n)1-ok(n), k=1,2,3,…,P (30) 对于隐层神经元,计算隐层的权值偏量值: (31) 按下式修改权值: (32) (33) 然后置n=n+1,输入新的数据向量,直到达到允许的条件为止。 为了防止出现局部极小值,加快收敛速度,在修改权值时加入动量项αΔvij(n-1)、αΔwjk(n-1)[7],且修改权值的学习步长由固定步长η改为变步长η(n),采用步长减小法[8]。权值改变量为 (34) (35) 其中: (36) 即学习步长随着输入数据组数的增加逐渐变小,SNR为信噪比,α取值为经验值0.9。 根据实际需要,在估计PN码的实验中,我们采用双极性sigmoid函数来作为神经元的激活函数,所以在此隐层的输出为 (37) 则: 2yj(n)1-yj(n) (38) 同理,输出层神经元的输出为 (39) 则有: (40) 2ok(n)1-ok(n) (41) 因此对应的权值调节公式要做相应的更改。首先对于输出层神经元,计算: (42) 对于隐层神经元,计算: j=1,2 (43) 权值改变量为 (44) (45) 所以权值修正公式为 i=1,2,3,…,P;j=1,2 (46) j=1,2;k=1,2,3,…,P (47) 等到神经网络达到收敛时,即达到允许的最小误码率,PN序列可通过第二层的权值向量恢复出来,这样就可以进一步恢复出信息码。此处的误码率为估计的PN序列与标准PN序列相对比后错误码位数与PN序列周期长度的比值。比如PN序列周期长度为P,估计出来的PN序列有d位码与标准PN序列码不同,则误码率为d/P。 本文方法利用误差反向传播来有监督地调节网络,输入信号为基带DS信号,期望输出向量d(n)是和输入数据向量一样的数据向量,即d(n)=x(n)。图中输入神经元的个数与输入信号向量x(n)的维数相同。 综上所述,改进的BP算法应用于神经网络来估计PN序列,其步骤简述如下: 第1步:网络初始化,置所有网络权值vij和wjk为均匀分布的1和-1,i=1,2,3,…,P;j=1,2;k=1,2,3,…,P,设置终止条件,即允许的最小误码率; 第2步:对于时刻n,输入新的数据向量x(n); 第3步:前向计算,根据式(37)和式(39)计算隐层和输出层神经元的输出; 第4步:根据式(40)计算误差; 第5步:反向计算,根据式(47)和式(42)计算隐层到输出层的权值和输出层的权值偏量; 第6步:反向计算,根据式(46)和式(43)计算输入层到隐层的权值和隐层的权值偏量; 第7步:置n=n+1,返回步骤2继续,直到达到允许的最小误码率为止。 以下所有实验的信号采样率Sa=8 bit/chip(即Tc=8Te,Te为采样周期)。 (1)实验一:验证BP神经网络估计PN序列的可行性 这里输入数据考虑一个BPSK数据模型,PN码长是100位,输入数据信号截断100位,截取第一个信息码扩频波形的后60位和第二个信息码扩频波形的前40位。信道噪声为高斯白噪声,信噪比SNR=-5 dB,时间窗口数即输入的数据组数N=100。如图3所示,PN序列是由PN序列发生器产生的100位标准PN序列码,网络权值1的前60位的符号函数值对应PN序列的后60位,网络权值2的后40位的符号函数值对应PN序列的前40位的反码。从图中可以看出,扩频序列可以从第二层网络权值中恢复出来。 图3 网络权值与PN序列对比Fig.3 Weights of the network compared with the PN sequence (2)实验二:验证该BP神经网络的收敛性能 图4为不同信噪比的情况下(从-6~0 dB)估计PN码的平均误码率随着数据组数的增加的变化曲线,即该神经网络的学习收敛曲线。该输入信号的PN码长为500位,截取第一个信息码扩频波形的后300位和第二个信息码扩频波形的前200位。该平均误码率的求法是对每一个信噪比的输入信号进行100次蒙特卡洛仿真然后求平均值得到的。从图中可以看出,当N逐渐增大时,误码率逐渐减小,最后变为0;且信噪比越高,误码率减小得越快。所以PN码估计的效果会随着N的增加而变好,且同一信号在高信噪比的情况下会收敛得更快。 图4 网络收敛曲线Fig.4 Convergence curve of network 图5是针对不同PN码长的输入信号,数据组数(完全收敛时所需的数据组数)的均值随输入信噪比的变化曲线。图6是针对不同PN码长的输入信号,数据组数(完全收敛时所需的数据组数)的方差随输入信噪比的变化曲线。这里设收敛误码率为0.02,即允许存在0.02的误码率,比如PN码长为100位,允许存在2位错误码的估计。在此,当PN码长为200位时,截断200位,截取第一个信息码扩频波形的后120位和第二个信息码扩频波形的前80位;当PN码长为500位时,截断500位,截取第一个信息码扩频波形的后300位和第二个信息码扩频波形的前200位;当PN码长为1 000位时,截断1 000位,截取第一个信息码扩频波形的后600位和第二个信息码扩频波形的前400位。 从图5可以看出,在PN码长和取样率确定时,信噪比越低则神经网络收敛所需的数据组数的均值就越大。而在信噪比相同时,以-9 dB为分界线,当信噪比小于-9 dB时,PN码越长则所需数据组数的均值就越小;当信噪比大于-9 dB时,则所需数据组数的均值差不多相同。 图5 数据组数的均值随信噪比的变化曲线Fig.5 Curves of mean number of data sets with SNR 图6 数据组数的方差随信噪比的变化曲线Fig.6 Curves of the variance of data sets with SNR 从图6中可以看出,在PN码长和取样率确定时,信噪比越低则神经网络收敛所需的数据组数的方差就越大,即估计的偏越大;而且在信噪比相同时,PN码越长则所需数据组数的方差就越小,尤其是在低信噪比的情况下更为明显。 从实验一和实验二的结果可以得出,本文的方法完全可以准确估计到DS信号的PN码序列,而且可以在较低信噪比的条件下实现估计。由图4、图5和图6可以看出,在信噪比相同时,PN码越长则所需数据组数的均值和方差就越小,即PN码越长则算法的估计性能也会越好。 本文提出了一种用BP神经网络来估计直扩信号PN序列的方法。该方法是基于反向传播(BP)神经网络,它的输入是接收到的信号,期望输出是和输入相同的数据,根据误差反向传播来有监督地调节网络,估计的PN序列值在第二层的权值上显示出来。本文采用改进的BP算法来运行网络,计算机仿真结果表明,该方法对PN序列可以得到很好估计,尤其是在低信噪比下对长伪码的估计会更有效。因此本文的方法将为解决DS信号PN序列的实时盲估计问题提供一种途径,为DS通信的管理、侦察和干扰以及DS-CDMA的盲多用户检测等铺平道路。对于优化神经网络,提高收敛速度,是以后需要深入研究的工作。 参考文献: [1] 江莉,李林,董惠,等.通信侦察中的伪码序列盲估计算法[J].现代防御技术,2009,37(3):85-89. JIANG Li, LI Lin, DONG Hui, et al. Blind Estimation Algorithm for PN Sequence in Communication Reconnaissance[J].Modern Defense Technology,2009,37(3):85-89.(in Chinese) [2] Dominique F, Reed J H. Simple PN Code Sequence Estimation and Synchronization Technique Using the Constrained Hebb Rule [J].Electronics Letters, 1997, 33(1): 37-38. [3] 张天骐,周正中.直扩信号的谱检测和神经网络估计[J].系统工程与电子技术,2001,23(12):12-15. ZHANG Tian-qi, ZHOU Zheng-zhong. Direct Sequence Spread Spectrum Signal Detection and Neural Network Estimation [J]. Systems Engineering and Electronics, 2001,23(12):12-15. (in Chinese) [4] 张天骐,林孝康,周正中.基于神经网络的低信噪比直扩信号扩频码的盲估计方法[J].电路与系统学报, 2007,10(2): 118-123. ZHANG Tian-qi,LIN Xiao-kang,ZHOU Zheng-zhong.A Neural Network Approach to Blind Estimation of PN Spreading Sequence in Lower SNR DS/SS Signals[J].Journal of Circuits and Systems,2007,10(2):118-123.(in Chinese) [5] Celine Bouder, Gilles Burel. Spread Spectrum Codes Identification by Neural Networks[C]//Proceedings of 4th World Multiconference on Cirulits,Systems,Communications & Computers.Vougliameni:[s.n.],2000:257-262. [6] 阎平凡,张长水.人工神经网络与模拟进化算法[M].北京:清华大学出版社,2006:19-27. YAN Ping-fan, ZHANG Chang-shui.Artificial Neural Networks and Evolutionary Computing[M].Beijing:Qinghua University Press, 2006:19-27.(in Chinese) [7] 刘希玉,刘弘. 人工神经网络与微粒群优化[M].北京:北京邮电大学出版社,2009:88-96. LIU Xi-yu, LIU Hong. Artificial Neural Network and Particle Swarm Optimization[M].Beijing:Beijing University of Posts and Telecommunications Press, 2009:88-96.(in Chinese) [8] 韩力群. 人工神经网络理论、设计及应用[M].北京:化学工业出版社,2002:43-56. HAN Li-qun.Artificial Neural Network Theory, Design and Application[M].Beijing:Chemical Industry Press, 2002:43-56.(in Chinese)

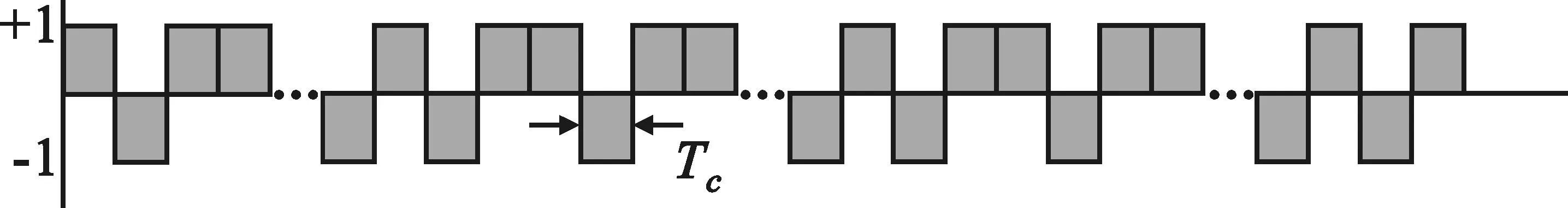
3.2 PN序列盲估计的BP神经网络实现



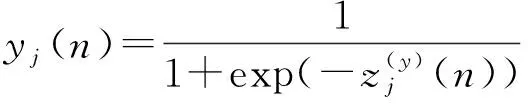
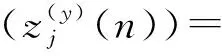

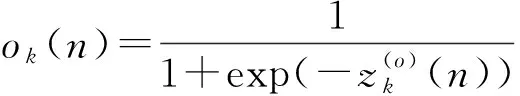
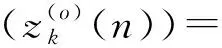


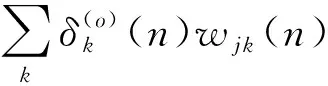

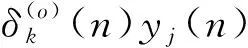
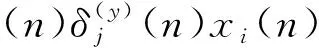

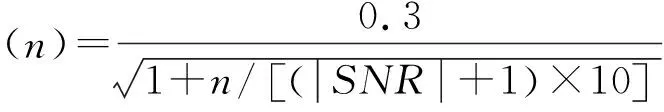
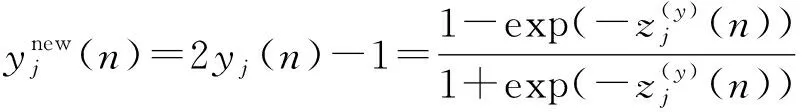


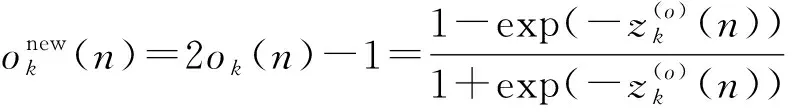


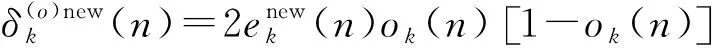

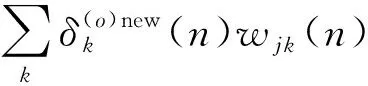
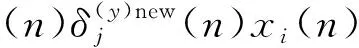
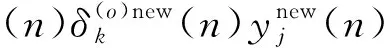
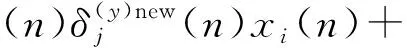


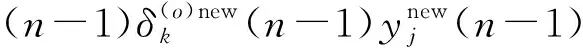
4 计算机仿真结果

5 结 论

