基于小波变换的神经网络模拟电路故障诊断

李 维

( 大连工业大学 信息科学与工程学院， 辽宁 大连 116034 )

0 引 言

电子线路是电子设备的核心，它的可靠性直接影响电子设备的可靠性。电子线路的故障诊断理论研究是保证电子设备设计质量的重要手段。在故障诊断中，突变信号往往对应设备的某种故障，分析和识别系统中产生的各种波形信号，并判别其状态，是进行模拟电路故障诊断的有效方法。设备正常运行时发出的信号较平稳，一旦设备出现故障，就将发出具有奇异性的动态非平稳信号，为实现设备故障的快速、准确检测，必须有效地识别故障发生瞬间的非平稳信号。

由于基于小波神经网络的故障诊断方法无需知道模拟电路故障的物理模型、组件容差和非线性特性，近年来已被用于模拟电路的故障诊断[1]，如BPNN、Hopfield网络和ART自组织网络等。为进一步提高故障诊断定位速度，获得更好的实时性，本文采用小波变换提取模拟电路故障信号的特征，以减小神经网络输入数目，从而简化神经网络结构，缩短检测时间和提高辨识故障类别的能力。信号的处理与分析是故障预测和诊断的基础，提高诊断的准确度，需要先进的信号处理和分析方法，小波变换以其对非平稳信号局部化分析及良好的定位功能，为故障诊断提供了新的分析手段。

1 小波变换及信号处理

小波变换的基本原理是通过小波母函数在尺度的伸缩和时域上的平移来分析信号，适当选择母函数可以使扩张函数具有较好的局部性，因此，它是一种时-频分析方法。在时-频域具有良好的局部化性质并具有多分辨分析的特性[2]，非常适合非平稳信号的奇异性分析，如利用连续小波变换可以检测信号的奇异性，区分信号突变和噪声；利用离散小波变换可以检测随机信号频率结构的突变。

1.1 Haar小波函数的定义及特性

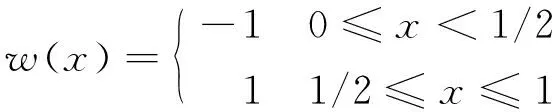
(1)

自变量x的定义域为[0，1]，对于任意一个信号f(x)可表示成不同尺度的Haar小波之和：

(2)

式中，f(x)为有限长度的信号，0≤x<1，ai为小波变换系数，w(x)为小波函数。

1.2 信号的奇异点与奇异性指数

从工程角度看，奇异点就是指信号中的突变点，奇异性则是关于奇异点突变程度的定性和定量描述。函数的突变点可以用它的可微性来表示，信号在突变点处是不可微的，同样对无限次可导的函数则称它没有奇异性。

对于任意信号f(x)，其小波变换定义为

Wf(ψ，x)=f*ψa，b(x)=

(3)

若函数f(x)[f(x)∈R]在某处间断或某阶导数不连续，则称该函数在此处有奇异性；若函数f(x)在其定义域有无限次导数，则称该函数是光滑的或没有奇异性。一个突变的信号在其突变点必然是奇异的。检测和识别信号的突变点并用奇异性指数Lipischitz来刻画它就是信号的奇异性检测理论。一个函数(或信号)f(x)∈R，设0≤a≤1，在点x0若存在常数K，对x0的邻域使得下式成立：|f(x)-f(x0)|≤K|x-x0|a，则称f(x)在点x0是Lipischitz。

如果a=1，则函数f(x)在x0是可微的，称f(x)没有奇异性；如果a=0，则函数f(x)在x0点间断。a越大说明奇异函数f(x)越接近规则，a越小说明奇异函数f(x)在x0处变化越尖锐。信号的奇异点可从小波变换的模极大值检测出来。小波变换的模极大值都出现在信号有突变的地方，而信号的突变点一定是信号的奇异点，即可能的故障点。

1.3 信号的分解及特征提取

在模拟集成电路故障诊断中，小波变换用来预处理采样信号，提取故障特征。在式(3)中令a=2j，b=k2j，(j，k)∈z2，则W(a，b)为二进小波变换，二进小波变换通过多分辨分析算法来实现，将信号f(x)分解为不同尺度上的低频概貌和高频细貌信号，分解公式为

(4)

将二进小波变换后各尺度空间的分解系数进行绝对值求和，按尺度顺序排列作为模拟电路故障特征向量，即：对采样信号进行N层二进小波分解，得到第1层到第N层，共N+1个小波分解系数序列{d1，d2，…，dN，cN}；对各层小波分解系数序列进行绝对值求和。设CN为第N层低频小波分解系数序列的绝对值之和，Dj为第j层高频小波分解系数序列的绝对值之和。特征向量构成是按尺度顺序以各层小波分解系数序列的绝对值之和为元素构成特征向量，即{D1，D2，…，DN，CN};标准化处理是通过变换处理将网络输入数据限制在[-1，1]区间内，从而避免较大的动态变化。

2 小波神经网络在模拟电路故障诊断中的应用

2.1 小波变换作为神经网络的预处理器

在模拟电路故障诊断中采用神经网络方法，是将所有的电路故障用1组唯一的特征来表示，这些特征与相关的故障类别一起作为输入(输出)送给神经网络，然后神经网络对它的权和偏置参数进行调解，以达到所要求的关系。在试验阶段神经网络得到了1组故障特征作为输入，并由该网络决定故障类别。这样神经网络的输入数目将是大量的，为此，利用小波变换作为神经网络的预处理器可以大大减少神经网络输入的数目，提高了辨识故障类别的能力。基于小波-神经网络的故障诊断流程图如图1所示。

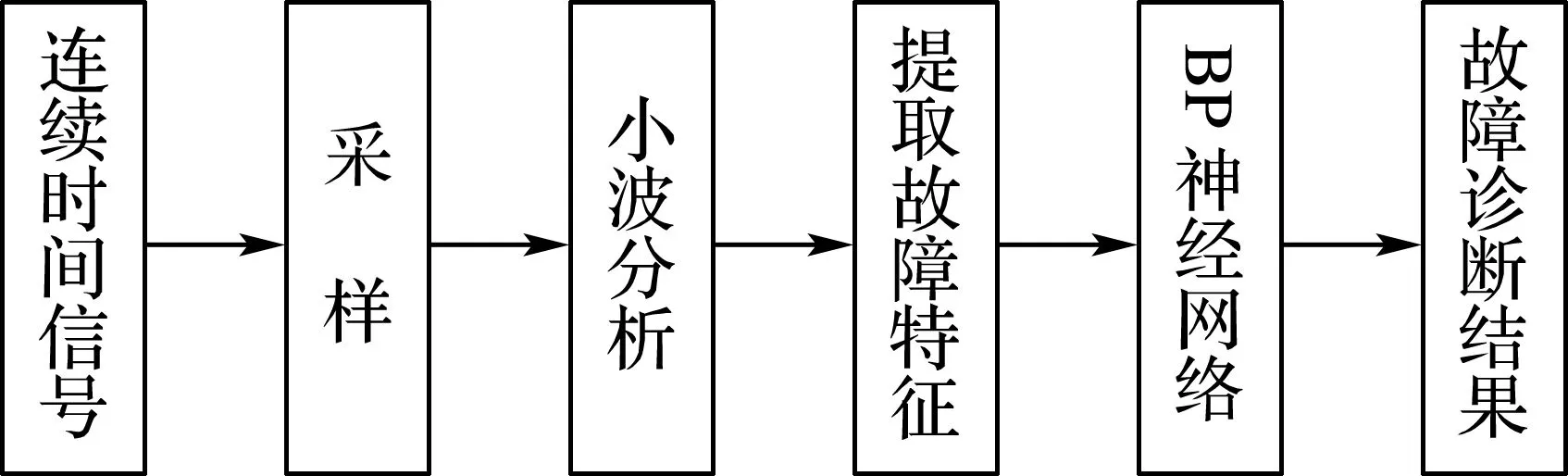
图1 小波-神经网络的故障诊断流程图Fig.1 Flow diagram of WNN fault diagnoses

小波分解是把原始信号分解为一个低频概貌信号和一个高频细貌信号，它是利用小波母函数的平移和伸缩实现的。低频概貌和高频细貌分别相应于信号大的尺度参数(低频段)和小的尺度参数(高频段)成分，所以小波分解可看成是信号形成低频和高频成分的产生过程。

2.2 模拟电路实例及故障特征选择

图2所示电路为某测试系统中的滤波电路，图中所示参数值为额定值。电路元件R1、C1、R2、C2均在容差范围内改变的情况属于无故障类(NF)。现只研究电路单一故障，即当这4个元件中的1个值高于或低于其额定值50%(分别用↑和↓表示)，而其他3个元件值均在容差范围内变化。这样，形成故障分类有8种(R1↑、R1↓、C1↑、C1↓、R2↑、R2↓、C2↑、C2↓)，它们与NF一起组成9种不同的电路工作状态，电路的冲激响应可通过一个窄脉冲来近似产生。

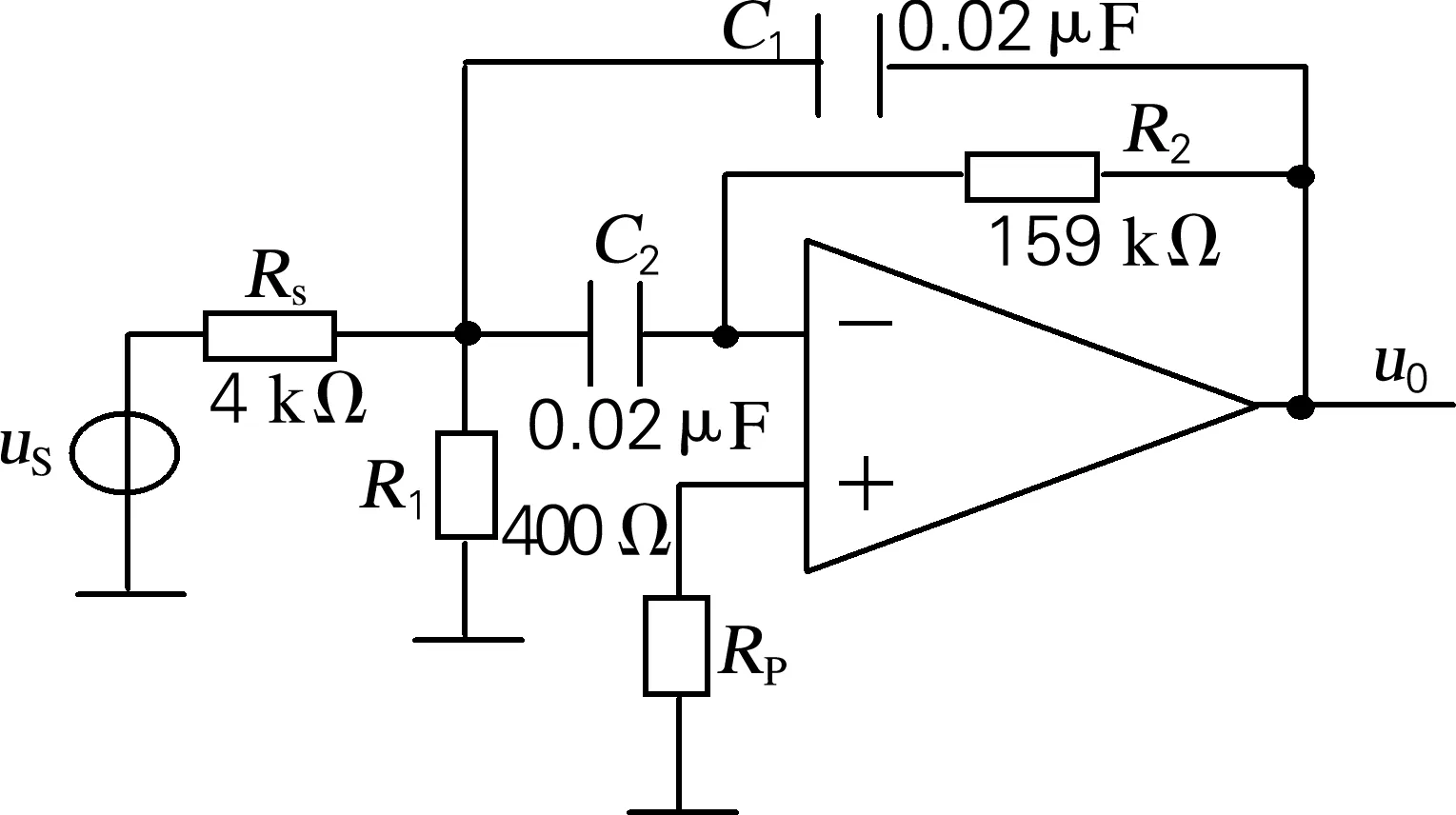
图2 滤波电路Fig.2 Filter circuit

故障电路冲激响应经二进制的小波变换式(4)分解为低频概貌系数CN和高频细貌系数Dj，这些细数分别反映了信号的低频和高频的内容。对图2每一层次的9种工作类别中对每一个类别由激励产生50个冲激响应，利用MATLAB小波分解仿真程序计算得到与这些冲激响应联系的低频概貌系数CN，即故障特征，它们为带状曲线，每一层有9条带状曲线分别对应9种不同的电路工作类别。然后对故障信号进行多层次分解，以实现对电路所有故障类别进行完全准确分类。针对该电路，神经网络结构参数为：输入层，神经元数目5个，即小波变换获得的故障特征向量；输出层，神经元数目9个，即电路故障模式；隐含层，神经元数目8个。神经网络的结构如图3所示。

在本例中，无小波处理时，神经网络结构为3层，输入节点数为49个，而采用小波预处理后结构变为2层，输入节点为5个。

图3 神经网络结构Fig.3 Neural networks structure

3 结 论

在模拟电路故障诊断中引入神经网络方法可大大改善其诊断能力，但神经网络的结构和输入数目很大，而采用小波变换做神经网络输入的预处理，使得神经网络的结构和神经网络的输入数目得到了简化，提高了辨识故障类别的能力，同时也改善了其工作性能。实例证明，采用小波预处理后神经网络结构的层数、输入节点数大大减少。

[1] 尉乃红. 基于神经网络的模型电路故障定位[M]. 武汉:华中理工大学出版社, 1996.

[2] 李清泉,张伟政,李彦明. 基于小波包的瞬变信号的提取[J]. 西安:西安交通大学学报, 2003, 22(4):43-46.

[3] 胡昌华,张军波,夏军,等. 基于Matlab的系统分析与设计—小波分析[M]. 西安:西安电子科技大学出版社, 1999.

[4] 谢宏,何怡刚,吴杰. 基于BPNN的非线性电阻网络故障诊断方法的研究[J]. 湖南大学学报, 2002, 29(6):87-90.