三自由度精密定位工作台的设计与运动学分析

贾晓辉，张大卫

(天津大学机械工程学院，天津 300072)

20世纪 90年代提出的纳米压印光刻技术同其他光刻技术相比具有分辨率高、制作成本低、生产效率高，适合产量化生产等优点，已成为下一代32纳米工艺的关键技术[1-3]．近年来，应用于纳米压印光刻技术的微纳定位系统的研究已引起各国科学家的高度重视，美国德克萨斯大学[4]，韩国机械与材料研究院[5-6]、国内华中科技大学[7]、西安交通大学[8]以及中国科学院[9]等科研院所均已在该领域开展了卓有成效的研究工作．

纳米压印定位系统分为被动调节和主动调节 2种类型[10]．现有的纳米压印定位系统大都属于被动调节类型，即利用机构本身的柔性来被动的适应模板和基片之间的不平行，范细秋[7]、严乐[8]等设计的定位系统中主动调整部分并没有涉及柔性结构而且也只有部分自由度实现了主动的调整，而完全意义上的主动调整型定位系统还较为鲜见，因此开展这方面的研究是十分必要的．

与传统的伺服电机驱动和精密丝杠传动相比，压电元件体积小、刚度大、位移分辨率高、响应快．而柔性铰链机构结构紧凑、无传动空程、无摩擦，适于组成结构简洁的超高精度定位系统[11]．因此压电陶瓷驱动的柔性并联机构以其分辨率高、运动灵活、动态特性良好等特点，广泛应用于超精密加工和微纳米操作等研究领域[12]．

基于此，笔者提出采用压电陶瓷驱动的柔性并联机构实现纳米压印过程中的精密定位，给出了该新型精密定位工作台的机械结构设计，并根据其伪刚体模型开展了运动学分析，提出了一种修正系数矩阵方法，提高所建数学模型的准确性．并通过有限元方法验证了该方法的有效性和所设计精密定位工作台的性能．

1 精密定位工作台的机构设计

并联机构具有高刚度、高精度、低惯量、结构紧凑、无误差积累等优点[13]，使其用作精密定位工作台时具有突出的优越性．由美国的 Tsai等[14]提出的改进 Delta机构中仅含有转动副，该转动副仅提供绕单轴的转动自由度．单自由度柔性铰链同样可以提供绕某固定轴的转动自由度，因此用单自由度柔性铰链代替传统改进 Delta机构中的回转副，并对并联结构的杆长进行调整，即可得到运动学性能与传统机构等效的柔性并联精密定位系统．笔者以改进的 Delta机构(见图 1)为基础，设计的一种新型纳米压印精密定位工作台，如图2所示．

图1 改进的Delta机构Fig.1 Modified Delta mechanism

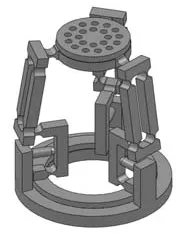
图2 精密定位工作台Fig.2 Precision positioning stage

在多种截面形式的柔性铰链中，圆形凹槽柔性铰链的变形精度最佳[15]，因此该精密定位工作台各关节位置采用单自由度圆形凹槽弹性铰链．

原则上讲，为了方便设计加工，各关节位置上的铰链通常会尽量选用同一系列，但在此类柔性定位工作台中，由于受整体构型以及材料应力极限的限制，在压印力作用下，主动臂上端的柔性铰链与其他位置上铰链相比，会首先达到应力极限，如图 3所示．因此为保证机构安全同时也为了提高机构高度方向上的刚度，在不影响整体构型的前提下将此处柔性铰链的刚度适度的提高．

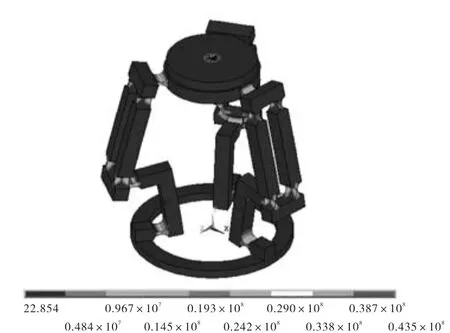
图3 应力分布示意(单位：N)Fig.3 Distribution of stress(unit：N)

根据悬臂梁柔度公式可知，两铰链之间的连杆越长，其柔度也就越大，那么相对于柔性铰链所表现的柔性而言，其对于柔性机构整体刚度的影响则不能忽略．具体在本文所涉及的柔性工作台中，如果连接主动臂两端铰链的连杆长度比较大，其表现出的柔性会令从动臂平行四边形上的柔性铰链不能形成有效的摆动，使得此处的柔性铰链形同虚设，从而造成与原有刚性机构运动学特性的不一致，引起运动学分析错误．针对这一点，在工作台的设计中恰当的分配长杆长度的同时将从动臂上的柔性铰链刚度适当降低，使其在保证机构整体刚度的同时又能形成明显的摆动，如图4所示．

图4 从动臂变形示意Fig.4 Distortion of the passive arm

采用 3个压电陶瓷驱动器推动主动臂来实现工作台沿 x、y 和 z 轴的平动自由度．考虑到压电陶瓷的脆性特性，在压电陶瓷和驱动点之间增加球形接头环节，以克服较大的弯矩作用在压电陶瓷驱动器上，避免其承受弯矩和拉力，保证压电陶瓷驱动器能够正常工作．由于采用了球形接头结构，从而使得压电陶瓷和驱动点的接触形式为赫兹接触．当压电陶瓷快速运动过程中，赫兹接触会使主动臂与压电陶瓷器驱动器分离，进而降低运动精度．为了克服这一缺点，需要对压电陶瓷施加一定的预紧力．通过调整压电陶瓷驱动器和支持之间的调整垫片，并借助柔性机构的弹性，即可实现对压电陶瓷驱动器的预紧．

由于该工作台采用柔性铰链代替回转副作为传动机构，因此，具有无机械摩擦、无间隙等特点．此外，由于该类工作台铰链处的位移以及工作台的工作空间都很小，使得并联机构固有的一些缺点，如非线性、位置运动学正解复杂、各运动支链驱动器之间的耦合等都得到了一定的改善．

2 运动学分析

在运动学分析过程中，将柔性铰链等效为传统的转动副，即不考虑柔性铰链转动过程中铰链中心点偏移的影响，建立精密定位工作台的伪刚体模型．同时，为了消除由于忽略柔性铰链中心偏移而带来的误差，进而提高所建运动学模型的准确性，引入了基于最小二乘法的修正矩阵方法对所得到的雅克比矩阵进行修正．

2.1 伪刚体运动学模型

伪刚体模型法将柔性机构等效为普通的刚性连杆机构后，再利用传统的刚性机构分析方法进行建模分析，是一种有效的柔性机构运动学分析方法．这种方法仅仅考虑柔性机构中各柔性铰链沿其运动方向上的刚度，而将其他方向上的柔性加以忽略．据此，在此类柔性定位工作台的分析中首先假设机构中只有柔性铰链产生绕轴向的弯曲弹性变形，且变形在其弹性极限范围之内，而其他构件及动平台则认为是刚性的．这样就可以将柔性铰链之间的连杆等效简化为刚性杆，将柔性铰链等效为转动副和线性扭簧，这样建立三自由度精密定位工作台机构单个支链的伪刚体模型如图5所示．

可以注意到，机构中各部分杆件的相对转动均绕着铰链转动轴线方向，因此建立如图 5所示的坐标系，将基平台的中心设为全局坐标系O-xyz 的坐标原点 O，y轴平行于基平台平面法线方向并指向动平台，x轴指向 OA1，z轴方向由右手坐标系确定．动平台的中心为 P，基平台和动平台半径分别为 r0和 r5，主动臂 AiBi(i=1，2，3)杆长为 r1，BiCi长度为 r2，从动平行四边形机构宽度为 2l，长度 CiDi为 r3，DiEi长度为 r4，αi为 OAi与全局坐标系 x轴的夹角，驱动臂的初始夹角为 γi，BiCi的初始夹角为βi，EiDi的初始夹角为ϕi．在各关节处建立局部坐标系，各坐标系的 z轴均与该处转动铰链的转轴方向平行，各铰链绕局部坐标系 z轴的相对转动表示为 θk,k-1i(k＝1，…，7)．根据坐标变换建立上述各坐标系间的矩阵转换关系为

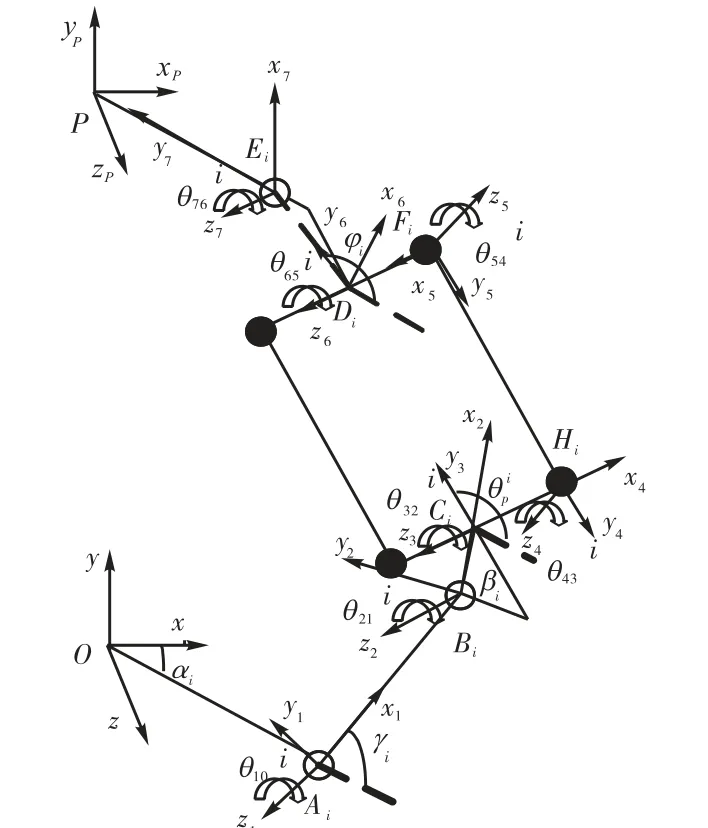
图5 单个支链伪刚体模型及坐标系设置Fig.5 Pseudo-rigid-body model and coordinate system of one kinematic chain

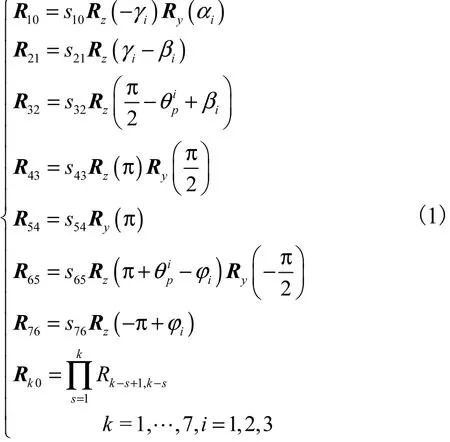
式中Ry(αi)为绕y轴转动αi角的基本旋转变换矩阵，其他类似，不再一一说明．

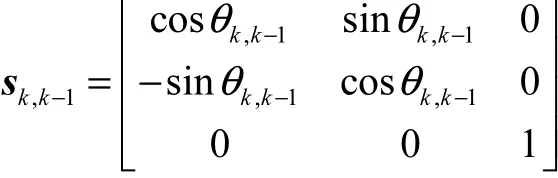
将动平台中心点 P在全局坐标系 O-xyz中的位置矢量表示为 P=(xP，yP，zP)T，从图 3所示单个支链各杆件之间的形位关系可以得到

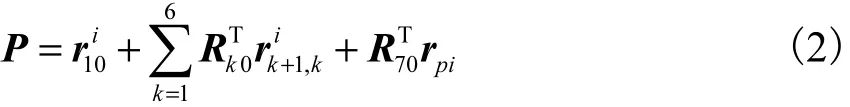
式中：r10＝r0yR(αi)u1，r21=r1u1，r32＝r2u1，r43=－lu3，r54i＝－r3u2，r65i=lu1，r76i＝r4u1，rPi=r5u2，ui(i＝1，2，3)为沿 x、y、z坐标轴的单位方向矢量．

由于工作台的工作空间及铰链处的运动范围很小，可将微小的相对偏转角的三角函数作线性化处理，即 cos θk,k-1i≈1，sin θk,k-1i≈θk,k-1i．由图 5 所示杆件BiCi、DiEi之间的形位关系，可以得到关系：θ21i=θ32i=θ65i=θ76i和 θ43i=θ54i，因此将式(2)简化消元后，可建立输出Δx、Δy、Δz与输入 θ10i之间的线性关系为

其中：J为雅克比矩阵且

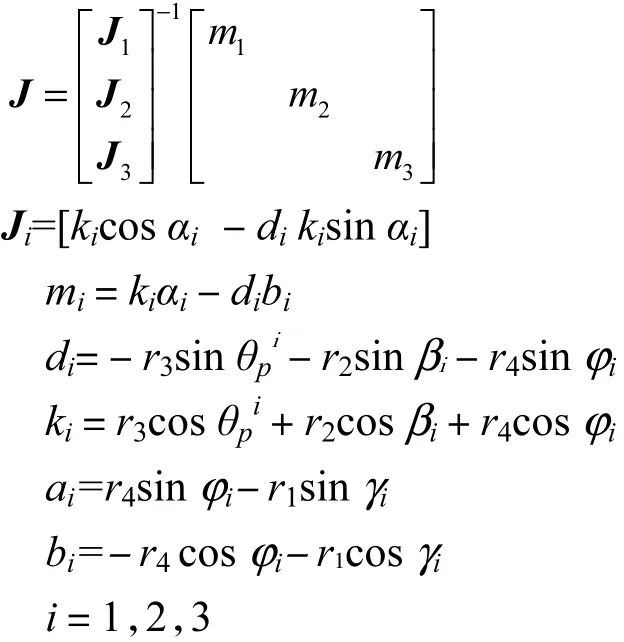
2.2 修正系数矩阵

在建立的机构运动学理论方程中引入修正系数矩阵 S，旨在消除由于柔性铰链中心偏移带来的误差，提高理论结果的准确性，该矩阵为

则式(3)可改写为

式(4)所示的修正系数矩阵可以利用最小二乘法分析动平台 P点的位置输出理论计算结果及仿真结果两者之间的偏差加以确定．这样动平台中心 P点分别沿全局坐标系 x、y、z轴 3个方向的位置误差xi、yi和zi平方和就可以表示为

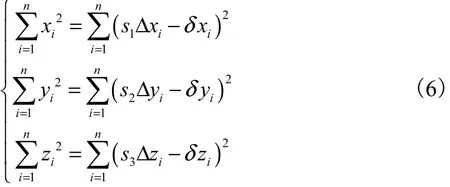
式中δ x、δ y、δ z为动平台中心P点实际值．

利用最小二乘原理求解式(6)得

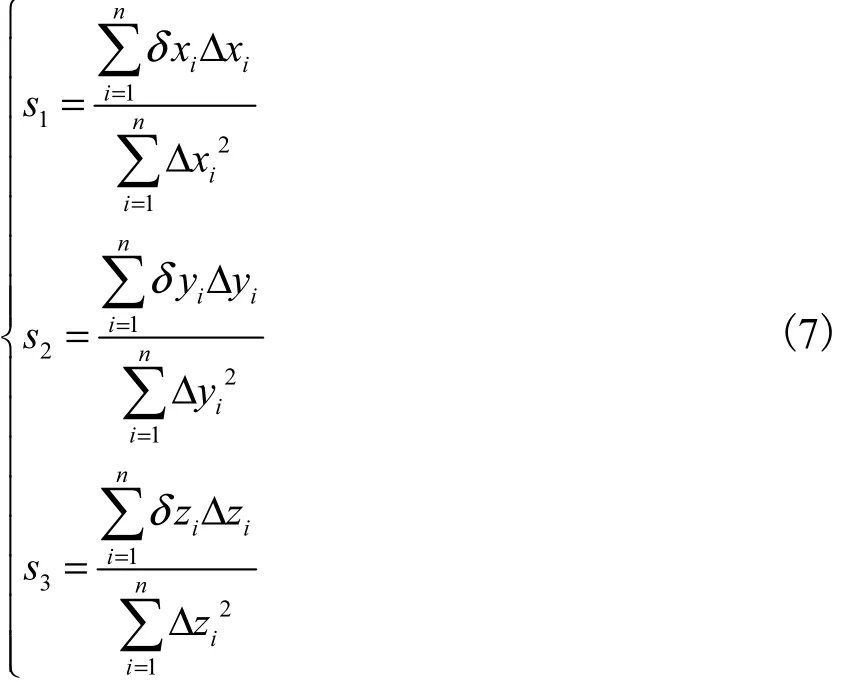
3 有限元仿真

利用有限元仿真软件 ANSYS对精密定位工作台进行有限元仿真分析来验证其性能．为了提高有限元计算精度，动平台、柔性铰链、连杆、底座均采用扫掠技术进行映射网格划分，在柔性铰链和动平台之间的圆环以及柔性铰链与基平台之间的连接处，采用自由网格划分来保证各个实体上单元节点的对应．柔性铰链有限元模型采用二次实体单元 Solid,95，定位工作台的其他部分则采用了 8节点的三维实体单元Solid,45．柔性铰链是精密定位工作台产生运动变形过程中变形最大的部分，因此将柔性铰链处的网格划分加密以提高计算精度．根据实际情况，模型材料选用弹簧钢65Mn，其弹性模量为210,GPa，泊松比0.27．结构参数分别为：r0=25,mm，r1=39.24,mm，r2=11.2,mm，r3=53.87,mm，r4=12.08,mm，r5=25,mm，θpi=98°，γi=75.6°，βi=49.4°，ϕi＝ 142.1°，α1=0°，α2=120°，α3=240°．

有限元仿真分析时，约束方式对仿真结果影响很大，约束方式应尽可能与实际使用中的约束情况一致，精密定位工作台在应用过程中把基座与机架固联，因而在本文仿真时，也对其做上述一致的约束．另外为了保证仿真的有效性又不失一般性，仿真时驱动位移垂直于驱动面且随时间递增．仿真过程分为2个步骤：

(1)分别对支链1、2、3施加按递增规律变化的位移载荷；

(2)对3个支链同时施加位移载荷，并且将3个支链上输入的位移量依次分为按递增规律变化的3段．

根据上述加载情况，进行有限元仿真分析，得到工作台中心P点在不同驱动位移作用下，沿全局坐标系 3个坐标轴方向上的偏移量，与式(3)中的理论结果比较，得出各方向上的位置偏移量关系曲线．为了确定修正系数矩阵，提取仿真过程中各支链主动臂输入偏转角求解理论计算值Δx、Δy、Δz，同时记录仿真过程中得到的动平台中心P点沿3个坐标轴方向的仿真值δx、δy、δz，代入式(7)得修正系数矩阵 S=diag(0.408 0.518 0.407)．利用修正系数矩阵将理论结果修正后，再与采集的仿真结果作比较，得到修正后各方向上的位置偏移量关系曲线，将之与前面得到的理论结果及采集的仿真值作比较(图 6～图 9)．要说明的是，理论计算中得出的输出量存在正负两种结果，但考虑到实际情况，Δy取负值显然是不合理的，所以将其忽略．另外为了便于观察，这里在两者符号一致的情况下均取其绝对值进行描述．

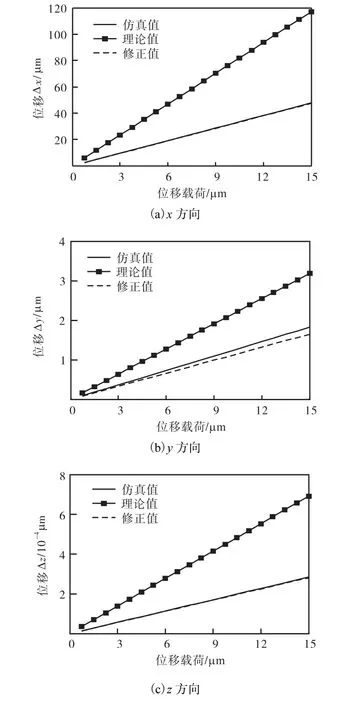
图6 仅驱动支链1时不同方向上3种位移结果比较Fig.6 Comparison of three results of displacement in different directions driven by link 1

图7 仅驱动支链2时不同方向上3种位移结果比较Fig.7 Comparison of three results of displacement in different directions driven by link 2

通过分析以上各图，可以得到结果如下．

(1)精密定位工作台中心P点的位置偏移量的理论计算结果与仿真结果误差比较大，但分布均匀，利用修正系数将其修正后，各方向上误差值均得到了有效降低．

(2)在保证机构有效的条件下，根据图6中所示，当仅驱动支链1时，沿x方向误差约为59.5%，沿y方向误差约为42.7%，沿z方向误差约为59.2%；利用修正系数修正后，沿x方向误差约为0.68%，沿y方向误差约为－10.6%，沿z方向误差约为－0.5%．

(3)根据图7中所示，当仅驱动支链2时，沿x方向误差约为57.7%，沿y方向误差约为45.6%，沿z方向误差约为 59.5%；利用修正系数修正后，沿 x方向误差约为－3.5%，沿y方向误差约为－4.93%，沿z方向误差约为0.34%．

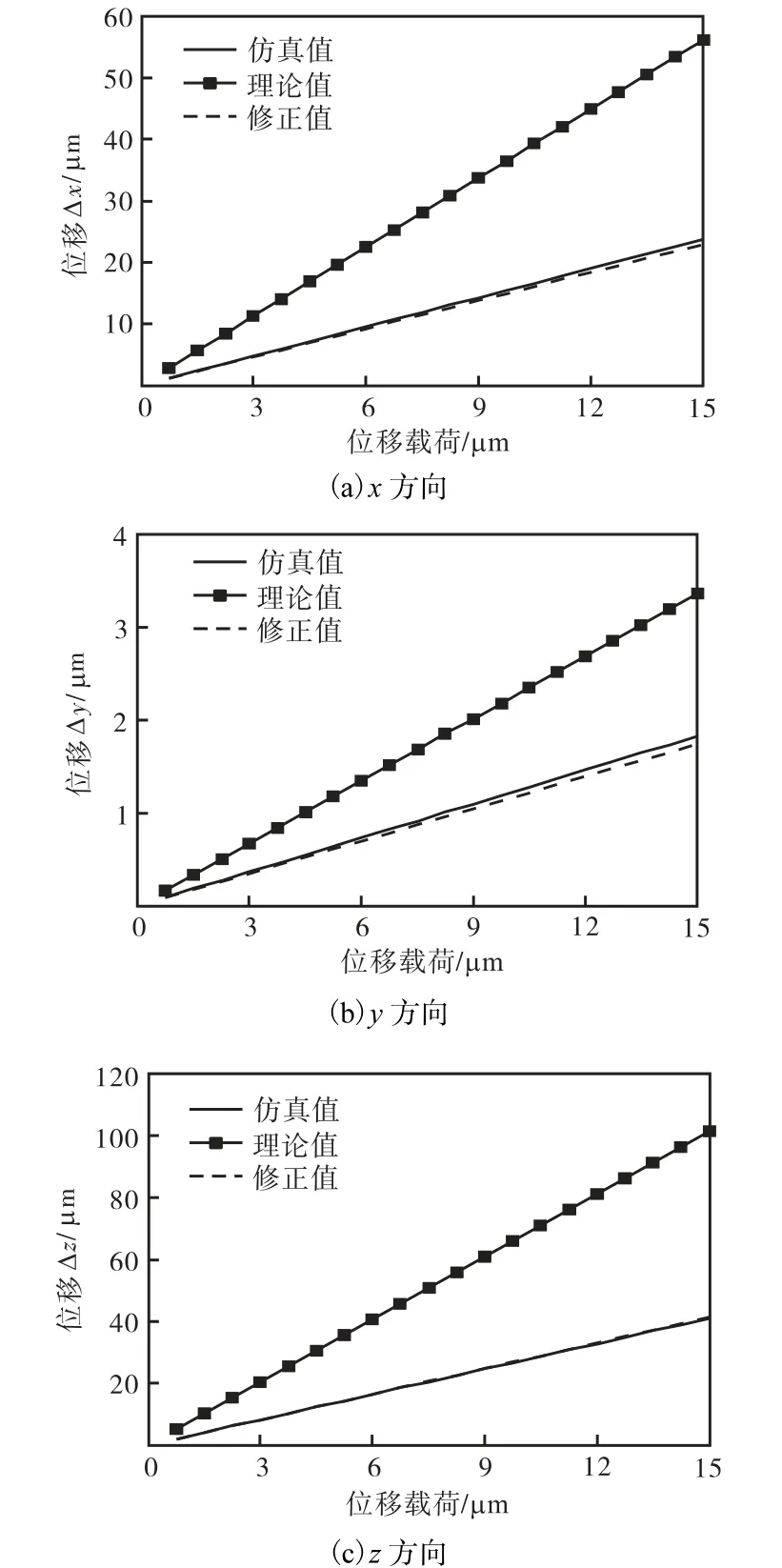
图8 仅驱动支链3时不同方向上3种位移结果比较Fig.8 Comparison of three results of displacement indifferent directions driven by link 3

(4)根据图8所示，当仅驱动支链3时，沿x方向误差约为57.7%，沿y方向误差约为45.6%，沿z方向误差约为 59.5%；利用修正系数修正后，沿 x方向误差约为－3.5%，沿y方向误差约为－4.93%，沿z方向误差约为0.34%．

(5)根据图9所示，当3个支链同时驱动时，沿x方向误差约为 59.3%，沿 y方向误差约为 48.3%，沿 z方向误差约为58.9%左右；利用修正系数修正后，沿x方向误差约为 0.3%，沿 y方向误差约为 0.21%，沿 z方向误差约为－1.1%．

(6)造成较大误差的原因除了 ANSYS中建模分网，方程简化等方面的原因外，根据“伪刚体模型”概念对空间并联柔性定位工作台机构建立理论模型时将长杆等效为刚性杆，忽略了其柔性特性对工作台中心位置的影响．另外柔性铰链具有多个方向上的柔度，但在进行伪刚体模型简化时，只主要考虑其单方向的转动柔度，而将其他方向上的柔度加以忽略，也是造成位置误差的主要因素．

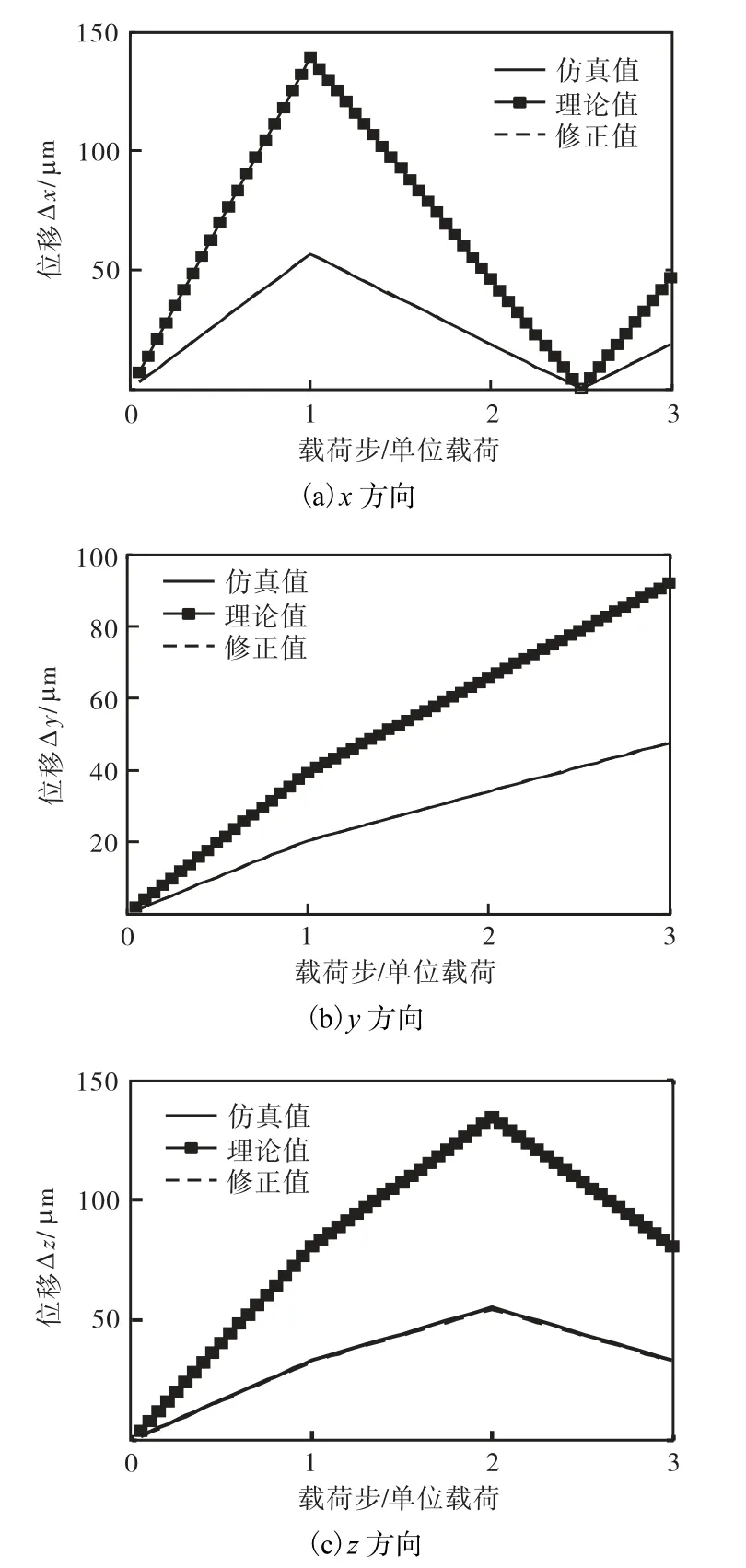
图9 3个支链同时驱动时不同方向上3种位移结果比较Fig.9 Comparison of three results of displacement in different directions driven by three links

4 结 语

笔者设计了一种可用于纳米压印工艺的柔性精密定位工作台，利用3个压电陶瓷驱动器实现工作台沿x、y、z轴3个平动自由度的主动调整．建立其伪刚体模型进行运动学分析，依据柔性机构特有的性能，将三角函数线性化以简化求解过程，得到了工作台输入转角与输出位移之间的线性表达式．为提高所建数学模型的准确度，引入修正系数矩阵对理论位移输出结果进行修正，有效的消除机构中长杆柔性及运动过程中柔性铰链中心偏移对工作台位移输出的影响，降低了位置误差．最后利用有限元分析工具对所设计的精密定位工作台进行仿真，验证了所建运动学模型的正确性．

［1］ Guo L J. Recent progress in nanoimprint technology and its applications[J]. Journal of Physics D：Applied Physics，2004，37(2)：123-141.

［2］ 刘彦伯，顾长庚，乌建中，等. 下一代实用光刻技术—纳米压印技术[J]. 机电一体化，2005，11(6)：14-19.

Liu Yanbo，Gu Changgeng，Wu Jianzhong，et al. The next generation lithograph：Nanoimprint lithography[J].Mechatronics，2005，11(6)：14-19 (in Chinese)．

［3］ Schulz H，Pavlicek H，Reng N. Step and flash nanoimprint lithography in Europe[C]// 2004 4th IEEE Conference on Nanotechnology. Munich，Germany，2004：655-656.

［4］ Choi B J，Sreenivasan S V，Johnson S，et al. Design of orientation stage for step and flash imprint lithography[J]. Precision Engineering，2001，25(3)：192-199.

［5］ Lee J J，Choi K B，Kim G H. Design and analysis of the single-step nanoimprinting lithography equipment for sub-100 nm linewidth[J]. Current Applied Physics，2006，6(6)：1007-1011.

［6］ Lee J J，Choi K B，Kim G H，et al. The UV-nanoimprint lithography with multi-head nanoimprinting unit for sub-50nm half-pitch patterns[C] // SIC-EICASE International Joint Conference．Busan，Korea，2006：4902-4904.

［7］ 范细秋，张鸿海，胡晓峰，等. 宽范围高对准精度纳米压印样机的研制[J]. 中国机械工程，2005，16(增)：64-67.

Fan Xiqiu，Zhang Honghai，Hu Xiaofeng，et al. A nanoimprint lithography prototype with wide working range and high precision alignment[J]. China Mechanical Engineering，2005，16(Suppl)：64-67(in Chinese)．

［8］ 严 乐，卢秉恒，丁玉成，等. 冷压印光刻工艺精密定位工作台的研制[J]. 中国机械工程，2004，15(1)：75-78.

Yan Le，Lu Bingheng，Ding Yucheng，et al. Highprecision orientation stage for room-temperature imprint lithography[J]. China Mechanical Engineering，2004，15(1)：75-78(in Chinese)．

［9］ 董晓文，司卫华，顾文琪. 气囊气缸式紫外纳米压印系统的设计[J]. 半导体光电，2007，28(5)：676-684.

Dong Xiaowen，Si Weihua，Gu Wenqi. Design of bellows cylinder type UV nanoimprint lithography system[J]. Semiconductor Optoelectronics，2007，28(5)：676-684(in Chinese)．

［10］ Lan H B，Ding Y C，Liu H Z，et al. Review of the wafer stage for nanoimprint lithography[J]. Microelectronic Engineering，2007，84(4)：684-688.

［11］ Tian Y，Shirinzadeh B，Zhang D. A flexure-based mechanism and control methodology for ultra-precision turning operation[J]. Precision Engineering，2009，33(2)：160-166.

［12］ Tian Y，Shirinzadeh B，Zhang D，et al. Design and forward kinematics of the compliant micro-manipulator with lever mechanisms[J]. Precision Engineering，2009，33(4)：466-475.

［13］ Tian Y，Shirinzadeh B，Zhang D，et al. Development and dynamic modeling of a flexure-based Scott-Russell mechanism for nano-manipulation[J]. Mechanical Systems and Signal Processing，2007，23(3)：957-978.

［14］ Tsai L，Stamper R E. A parallel manipulator with only translational degrees of freedom MECH：1152[C]//Proceedings of the 1996 ASME Design Engineering Technical Conference． Baltimore，USA，1996.

［15］ Tian Y，Shirinzadeh B，Zhang D，et al. Forward kinematics and solution methodologies for a flexurebased micro-manipulator[C]// 1st International Conference on Intelligent Robotics and Applications．Wuhan，China，2008，5315：250-259.