地下径流退水过程规律
李建柱,冯 平,王 勇
(1. 天津大学建筑工程学院,天津 300072;2. 天津市水文水资源勘测管理中心,天津 300061)
地下径流退水过程是指在降雨很少或无降雨时期内连续的排水和消退过程,是水文过程的重要组成部分[1].对退水过程的认识也是研究流域水量平衡和流域水文响应的重要内容之一.如果不考虑流域的降雨入渗、蒸发和地下水开采等因素的影响,流域的退水曲线可根据蓄水量和出流量之间的关系,并结合连续性方程建立出流量和时间的关系[2],这种关系可以用于枯水季节径流预测[3-5]、水文模型中地下径流的汇流计算[6]、水资源评价、规划与管理,以及面向灌溉、供水、地下水资源估算等的短期预报[7-8].
在实际应用中,通常把地下水退水流量和含水层蓄量之间表示为线性关系,从而推导出流域地下径流的退水过程,但是不同的流域,其地下径流的退水过程规律不一定相同,需要从实测资料进行分析.因此,笔者选择实测径流资料较全的滦河流域子流域(柳河和瀑河流域)的一组退水过程来进行分析,确定其地下径流的退水规律.
1 流域概况
滦河流域位于华北平原东北部,流经内蒙古、辽宁、河北三省、自治区的 27个县、旗、区,于河北省乐亭县兜网铺注入渤海,全长 888,km.流域面积44,750,km2,其中山区占 98%,平原占 2%.流域降水量年内分配不均,冬季仅占全年的 1%~2%,春季占9%,夏季占 67%~76%,秋季占 11%~19%.雨热同期.降水量年际变化也很大,年降水变率在 14%~26%之间.流域内地形差异很大,高原、山地、丘陵、平原以及河谷、盆地等各自形成小气候区.坝上、坝下因地势跌落明显,气候截然不同.坝上为高原气候,坝下山地、丘陵、河谷、盆地气候多样.山地中迎风坡降雨多,背风坡降雨少.
柳河和瀑河是滦河的支流,柳河发源于承德市兴隆县八拨子岭西北麓二道沟,在柳河口滦河右岸汇入滦河,河长 86,km,流域面积 1,020,km2.瀑河发源于平泉县石拉哈沟乡七老图山南麓,在宽城县滦河左岸瀑河口汇入滦河,河长 114,km,流域面积1,990,km2(见图1),2个流域气候和气象条件相似,多年平均降水量 600,mm 左右.由于降水集中,径流年内变化很大,汛期水量较多,占年总量的一半以上.尤其是 7、8月份更集中,常出现短历时、大强度、笼罩面积小的局部暴雨,并由此形成洪水,其洪水具有峰高量小的特征.
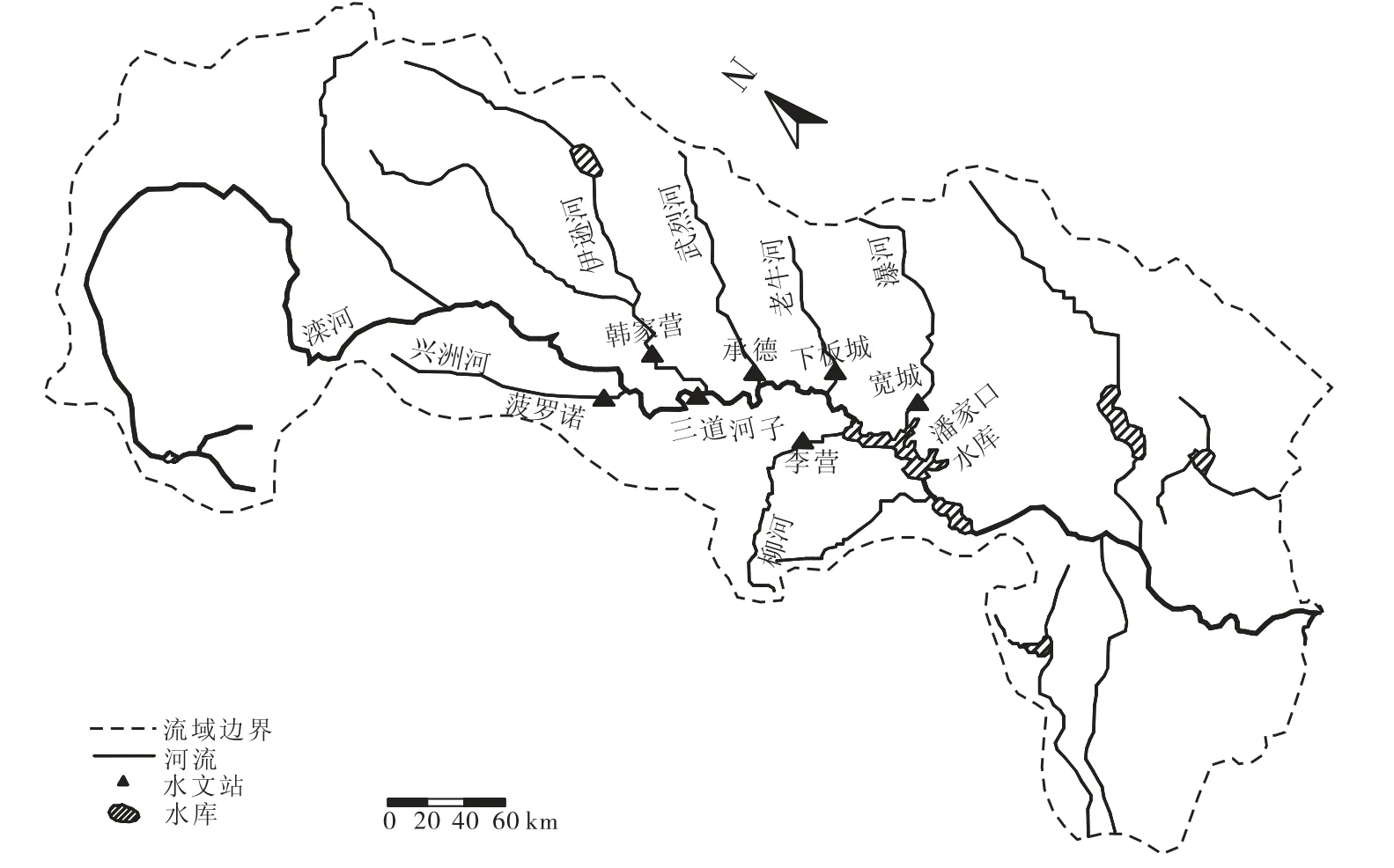
图1 滦河及其支流位置Fig.1 Sketch of Luanhe watershed and its tributaries
2 常用地下径流退水过程表达方法
假定退水流量和含水层蓄水量之间的几种关系,可以推导出不同形式的退水流量随时间的变化关系如下.
2.1 退水流量和含水层蓄水量呈线性关系
退水流量和含水层蓄水量的线性关系可表示为

式中:Q为退水流量,m3/s;S为含水层蓄水量,m3;k为待定参数,k越大,表示含水层的水力传导度越大.
联合连续性方程为

由此可求得退水方程为

式中Q0为退水曲线的初始流量,m3/s.
2.2 退水流量和含水层蓄水量呈指数关系
退水流量和含水层蓄水量的指数关系为

式中:D为含水层缺水量,m3;QB和φ为待定参数.
联立连续性方程,可求得退水方程为

2.3 退水流量和含水层蓄水量呈幂函数关系
退水流量和含水层蓄水量的幂函数关系[9]为

联立连续性方程,可求得退水方程为
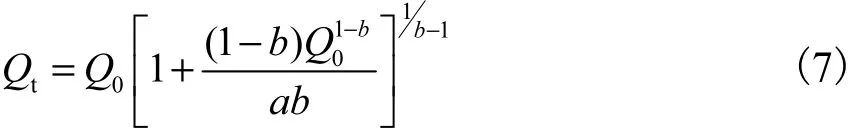
式中a、b为待定参数,可通过以下步骤来求出.
(1)假定一个b值;
(2)在流域退水曲线上,每隔一个时间步长tΔ取2个相邻的流量1iQ−和iQ,根据下式求出a的一个估计值

(3)对于退水曲线上不同的相邻流量,就会得到一个关于a的不同估计值,所有的估计值构成一个序列,其均值和方差分别为a(b)和 Cv[a(b ) ];
(4)在 0和 1之间对b值进行系统取样,根据以上步骤计算出相应的均值和方差;
(5)对应着最小的方差值的a(b)和b被选作2个参数的最优值.

模型的精度用 Powell提出的损失函数来评定,该方法将选择的所有场次洪水的退水过程综合考虑,能对各种模型的精度进行对比,即式中:ijr为第i条退水曲线第j个时间段模拟与实测出流量的相对误差;in为第i条退水曲线观测数据的个数;rn为选取退水曲线的条数.损失函数值越小,表明模型精度越高.利用选择的退水曲线率定模型中的参数,然后用每个模型模拟退水过程,比较模型的精度,从而确定流域的退水规律.
另外,还有退水流量和含水层蓄水量呈2个并联线性水库关系或串联线性水库关系的假定.
3 地下径流退水曲线的图形分析
图形分析是对线性水库退水和指数退水而言的.如果退水曲线符合线性水库假定,则一组退水曲线在ln Q -t图中表现为平行的直线.直线的斜率为
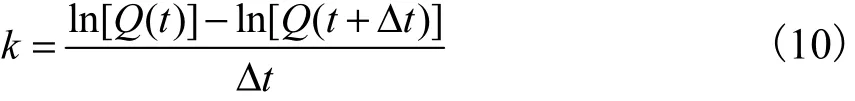
如果退水曲线服从指数假定,则一组退水曲线在Q-1-t关系图中表现为平行直线.直线的斜率为

选择柳河和瀑河的地下径流退水曲线,原则是:从一次洪水退水曲线的转折点开始到径流开始起涨点结束,中间时段每小时降雨量不超过 0.1,mm,这样,从柳河和瀑河流域分别选取了4次和6次地下径流退水过程,并绘在ln Q,-t和Q-1-t关系图上,如图2和图3所示.
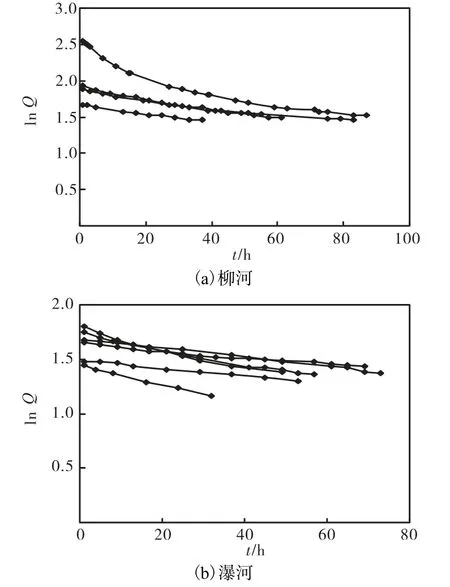
图2 地下径流退水过程的lnQ -t关系Fig.2 ln Q -t of groundwater recession processes
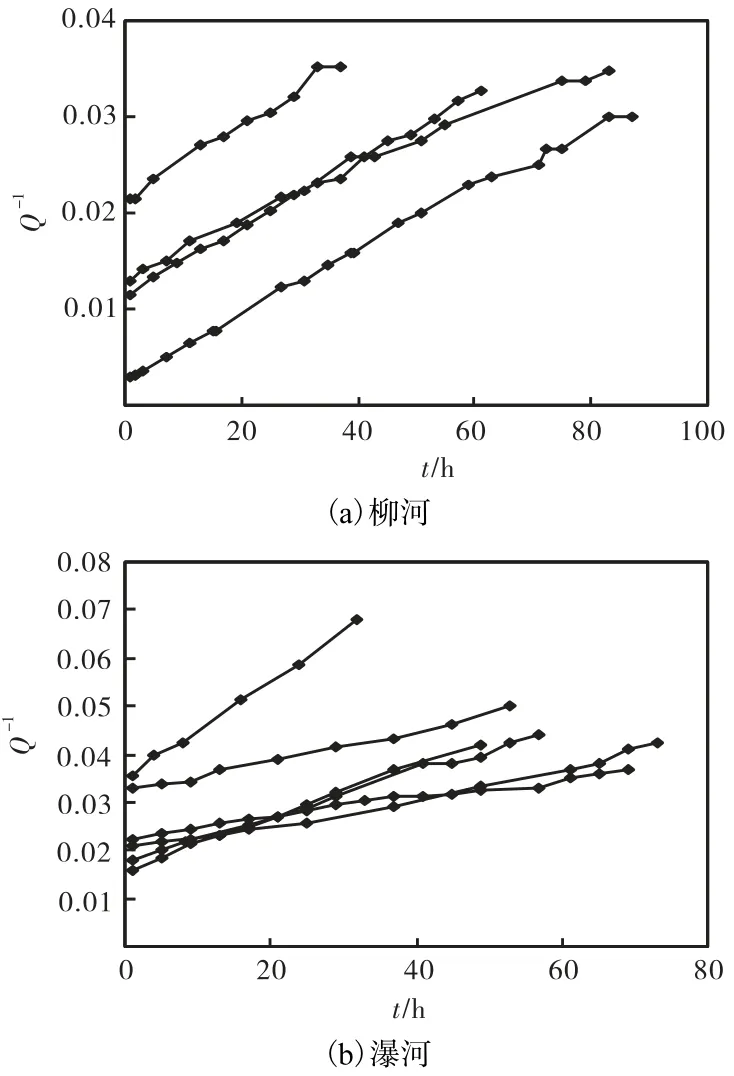
图3 地下径流退水过程的Q-1-t关系Fig.3 Q-1-t ,groundwater recession processes
从图2和图3可以看出,柳河流域地下径流退水过程在ln Q,-t图上并不是直线,而在Q-1-t关系图上,则表现为一组平行的直线,因此,可以初步判定其退水过程服从指数退水规律.瀑河流域的地下径流退水过程基本服从线性水库退水假定,但是在ln Q,-t图上直线的斜率表现为2组不同的情况,其中3次退水过程的斜率较大,另外 3次退水过程的斜率较小.这与Zillgens分析的结果一致 .经分析这2组退水过程之前产生的降雨过程可知,强度大、历时短的降雨过程产生的地下径流退水过程在 ln Q,-t图上的斜率小,而强度小、历时长的降雨过程产生的地下径流退水过程在 ln Q,-t图上的斜率大.这主要是因为随着降雨历时的增长,流域中饱和面积不断增大,地下水的补给越来越多.而短历时降雨过程下渗的水量大部分补充了非饱和带,并没有或很少形成地下径流.
4 地下径流退水过程的模型模拟分析
由于图形分析的方法不能反映非线性水库退水等复杂的退水过程,需要采用模型模拟的方法,对比模型模拟的精度来确定流域地下径流到底服从哪种退水规律.将前面所述的线性水库模型、指数模型和非线性水库模型应用于滦河水系子流域柳河流域和瀑河流域的地下径流退水过程模拟,模型参数采用式(10)和式(11)计算.线性水库模型求得的柳河k值范围在 0.012~0.017之间,平均值为 0.014,瀑河 k值范围较大,在0.006,9~0.020 0之间,主要受降雨类型的影响.将瀑河流域的地下径流退水分为 2类:①强度大(大于20,mm/h)、历时短(小于6,h)的降雨对应的k的平均值为 0.008,2;②强度小(小于 20,mm/h)、历时长(大于6,h)的降雨对应的k的平均值为0.019.
指数模型求得柳河φ 值范围在 2.63×10-4~3.89×10-4之间,平均值为 3.32×10-4,瀑河φ 值范围比较大,在 2.10×10-4~1.03×10-3之间,同样受降雨类型的影响.强度大、历时短的降雨对应的φ的平均值为2.75×10-4,强度小、历时长的降雨对应的φ的平均值为6.80×10-4.
用非线性模型求得的柳河,β,值为 0.56,α范围在758.37~1,022.22之间,平均值为 891.68,瀑河α值范围较大,在 421.86~1,569.58之间,其取值受降雨类型的影响.强度大、历时短的降雨对应的α的平均值为 1,228.99,强度小、历时长的降雨对应的α的平均值为 563.57.模拟各次地下径流退水过程时用计算所得参数的平均值.表 1和表 2列出了各个模型在模拟柳河和瀑河地下径流退水过程的参数值.图 4~图6以及表3是用不同方法模拟的结果.

表1 柳河地下径流退水过程模拟参数值Tab.1 Simulation parameters of groundwater recession in Liuhe sub-watershed
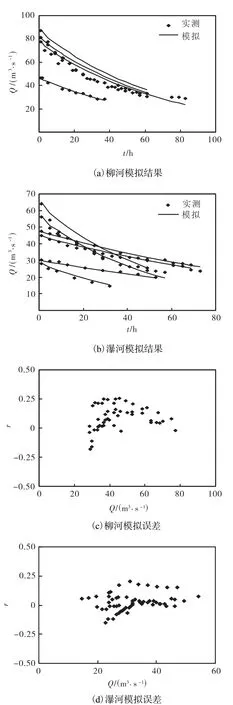
图4 地下径流退水过程线性水库模型模拟结果Fig.4 Simulation results of groundwater recession with linear reservoir model
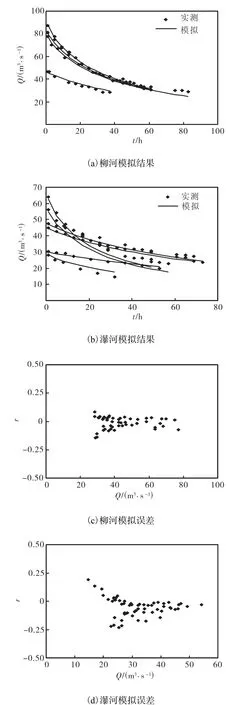
图5 地下径流退水过程指数模型模拟结果Fig.5 Simulation results of groundwater recession with exponential model
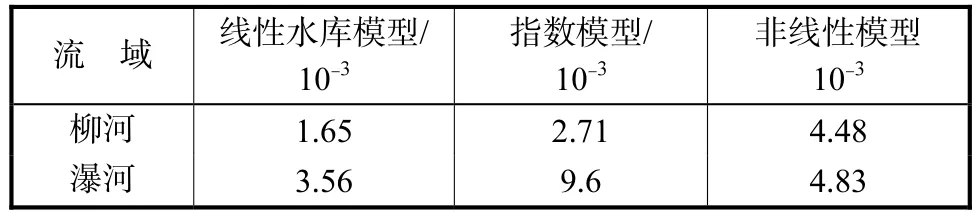
表3 不同模型损失函数值Tab.3 Values of loss function in three models
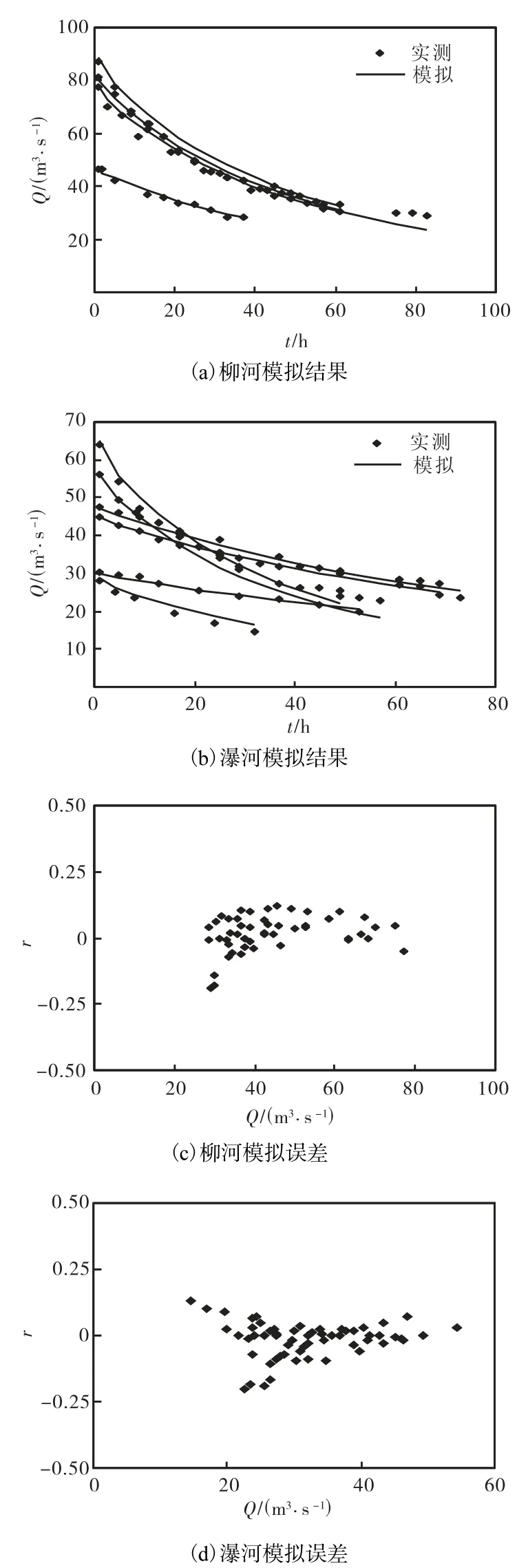
图6 地下径流退水过程非线性模型模拟结果Fig.6 Simulation results of groundwater recession with non-linear reservoir model
从退水模拟结果图上并不能清楚地辨别各个模型模拟效果的优劣,但是从模拟误差分析图上可以看出,在柳河流域,指数模型模拟的误差值在0左右小幅度摆动,最大相对误差为-0.14,比线性水库模型和非线性模型模拟效果更好.而在瀑河流域,线性水库模型比指数模型和非线性模型模拟效果稍好,这从表 3也可以看出,但是线性水库模型对其中一次洪水地下径流退水过程的模拟误差较大,最大误差达到0.2.
5 结 论
(1)从退水曲线在图中的表现形式来看,柳河流域地下径流的退水过程在指数图中呈一组平行的直线,而在瀑河流域,其地下径流的退水过程在 ln Q,-t图中表现为一组平行的直线,这说明,柳河流域的地下径流退水服从指数退水规律,瀑河流域地下径流退水服从线性水库退水规律.
(2)在选取的地下径流退水过程中,在瀑河流域,其退水常数分为2组不同的情况,主要受降雨特性的影响.降雨强度越大、历时越短,不同模型中的参数k、φ、b值越小,而 a值越大;反之,降雨强度越小、历时越长,不同模型中的参数 k、φ、b值越大,而 a值越小.
(3)从模型模拟的结果及其误差来看,柳河流域用指数模型模拟的误差较小,瀑河流域用线性水库模型模拟的结果较好,非线性模型模拟的误差处于线性水库和指数模型模拟的误差范围之内,这定量说明了2个子流域地下径流的退水规律.
[1] 李发东,宋献方,刘昌明,等. 华北典型山区坡地径流的退水过程研究[J]. 北京林业大学学报,2006,28(2):79-84.
Li Fadong,Song Xianfang,Liu Changming,et al.Discharge recession from runoff plots in representative mountain area in North China [J]. Journal of Beijing Forestry University,2006,28(2):79-84(in Chinese).
[2] Moore R D. Storage-outflow modeling of streamflow recessions,with application to a shallow-soil forested catchment [J]. Journal of Hydrology,1997,198(3):260-270.
[3] David B,Justin G H,James T M. Base flow recession rates,low flows,and hydrologic features of small watersheds in Pennsylvania,USA [J]. Journal of the American Water Resources Association,2005,41(5):685-697.
[4] Warren A G,Mandy J R,Ellen J C,et al. Use of streamflow data to estimate base flow/ground-water recharge for Wisconsin[J]. Journal of the American Water Resources Association,2007,43(1):95-113.
[5] Vogel R M,Kroll C N. Regional geohydrologicgeomorphic relationships for the estimation of low flow statistics [J]. Water Resources Research,1992,28(11):2451-2458.
[6] Harlin J. Development of a process oriented calibration scheme for the HBV hydrological model[J]. Nordic Hydrology,1991,22(1):15-36.
[7] Gurudeo A T,Mahbub I. Exponential smoothing method of base flow separation and its impact on continuous loss estimates[J]. American Journal of Environmental Sciences,2008,4(2):136-144.
[8] Smakhtin V U. Low flow hydrology:A review [J].Journal of Hydrology,2001,240(2):147-186.
[9] Wittenberg H. Baseflow recession and recharge as nonlinear storage processes [J]. Hydrological Processes,1995,13(5):715-726.
[10] Zillgens B,Merz B,Kirnbauer R,et al. Analysis of the runoff response of an Alpine catchment at different scales [J]. Hydrology and Earth System Sciences,2007,11(4):1441-1454.
[11] 熊立华,郭生练. 采用非线性水库假设的基流分割方法及应用[J]. 武汉大学学报,2005,38(1):27-29.
Xiong Lihua,Guo Shenglian. A baseflow separation method based on nonlinear reservoir assumption [J].Engineering Journal of Wuhan University,2005,38(1):27-29(in Chinese).

