基于T-S模糊模型的不确定非线性系统的容错保成本控制

费向阳，封文娟，张国山

(天津大学电气与自动化工程学院，天津 300072)

设备运行的可靠性越来越引起人们的重视．容错控制作为提高控制系统可靠性的一个重要手段，已成为控制理论研究的一大热点．近年来，出现了许多有关系统容错控制的研究成果[1-5]．对于不确定系统保成本的控制也引起了众多学者的关注，基于 Riccati方程和线性矩阵不等式(linear matrix inequality，LMI)的处理方法取得了许多有价值的结果[6-9]，其中文献[6]研究了保成本及最优控制器的设计及滤波问题，文献[7]推广了文献[6]的结果，研究了范数有界不确定系统带有时间乘积的保成本控制问题，该成本函数使系统状态快速趋于零而暂态响应时间缩短．文献[8]研究了离散时间不确定系统基于状态反馈与静态输出反馈的鲁棒二次保成本控制，通过 LMI给出控制律保证闭环系统稳定且成本函数有上界．文献[9]对于给定的二次成本函数，研究了一类时滞系统具有有界参数不确定的无记忆状态反馈保成本控制问题，通过基于 LMI的凸优化方法求得控制器使成本最小．

当被控对象含有时滞和不确定性时，往往还含有不同程度的非线性，难以建立精确的数学模型．因此近年来，已有一些采用T-S模糊模型研究状态或控制带有时滞的不确定非线性系统的容错与保成本控制问题论文，如文献[10]应用 LMI方法，对一类带有时滞不确定的模糊系统进行控制器设计，并且使得该模糊控制器能保证闭环系统稳定和二次型性能指标具有上界．文献[11]研究了基于状态反馈与动态输出反馈的非线性时滞系统 T-S模糊模型的保成本控制问题，通过平行分布补偿(PDC)方法，及时滞相关Lyapunov函数方法，给出了个控制器存在的充分条件，使用凸优化获得系统保持稳定时的时滞的上界，并给出了成本函数次优上界的最小化方法．文献[12]研究了状态具有变时滞的非线性系统的 T-S模糊模型的保成本控制问题，使用基于 LMI的凸优化方法，给出了基于状态反馈与基于观测器的输出反馈的保成本控制器的设计．文献[13]给出了 T-S模糊系统的非脆弱保性能控制器存在的充分条件，并且使系统H2性能最小化同时具有期望的H∞指标下的干扰抑制作用．文献[14]研究了不确定时滞系统的鲁棒容错控制问题，基于T-S模糊模型，利用Lyapunov稳定性理论与 LMI， 给出了对于传感器和执行器故障的鲁棒容错控制方法．但就笔者所知，目前鲜有针对基于T-S模糊模型、带有控制滞后的非线性系统的保成本容错控制问题的研究．因此，研究带有控制滞后的不确定时滞系统的模糊保成本容错控制具有一定的理论和实际意义．

为此，针对一类带有控制和状态滞后的不确定非线性时滞系统，基于 T-S模型，笔者研究了系统在执行器故障时的保成本容错控制问题，导出了状态反馈保成本控制器存在的充分条件，该条件保证了对所有允许不确定性，闭环系统是渐近稳定的，且对于一个给定的二次型成本函数，能保证闭环成本值不超过某个界．所得结论均以线性矩阵不等式的形式给出，应用Matlab中的LMI工具箱，给出了最优保成本控制器的设计并通过仿真验证了所给方法的有效性．

1 问题描述

考虑由如下 T-S模糊模型所描述的具有控制与状态滞后的不确定非线性时滞系统

Ri：MipThen

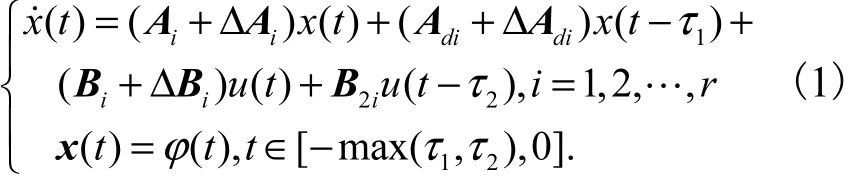
式中：Ri表示 T-S模糊模型的第i条规则，也称为模糊子系统；z1( t),z2(t),… ,zp(t)为模糊规则的前件变量；Mij为模糊语言集合； x ( t) ∈ Rn和 u ( t) ∈ Rm分别为系统的状态向量和控制向量．Ai、Adi、Bi和 B2i为已知的有适当维数的实矩阵，ΔAi、ΔAdi和ΔBi为不确定性矩阵函数，它们反映了系统模型中的不确定性；τ1＞0、 τ2＞0为滞后时间常数；ϕ(t)为实值连续向量函数．

假设不确定性是范数有界的，且满足

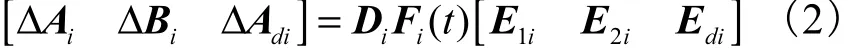
式中：Di、Ε1i、E2i和Edi为已知的具有适当维数的常数实矩阵；Fi( t)为一个具有 Lebesgue可测元的未知矩阵，且满足

应用单点模糊化、乘积推理和中心加权反模糊化推理方法[15]，可得全局模糊系统模型为

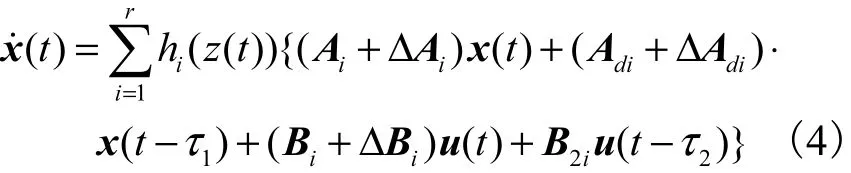
式中

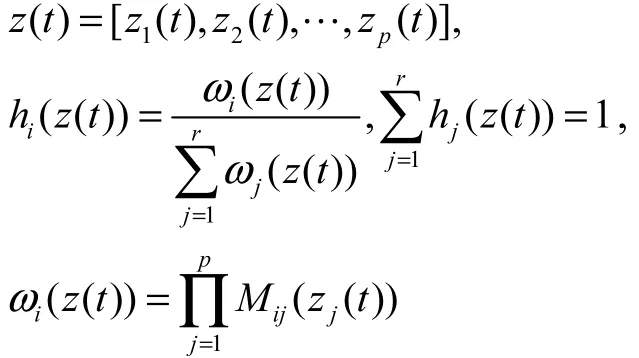
Mij( zj(t))表示前件变量 zj(t)对应于模糊值 Mij的隶属度．

对系统(1)定义成本函数为

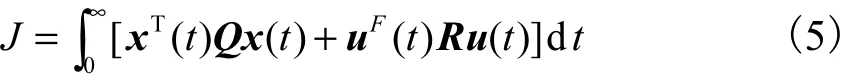
其中0＞Q和0＞R是给定的加权矩阵．

基于平行分布补偿(PDC)[16]，本文考虑如下关于模糊系统式(4)的模糊无记忆状态反馈控制律

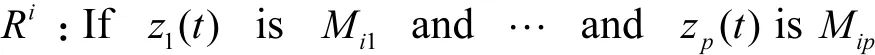
Then

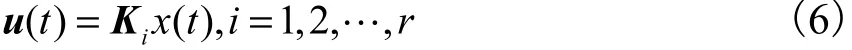
全局状态控制器可以表示为

控制系统在运行的过程中，由于某些元件出现故障会导致系统失效，因此定义某执行器输出恒为零时为该执行器失效，引入表示执行器发生故障的开关矩阵iL，其形式为

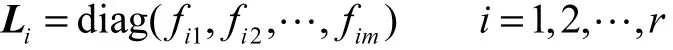
式中

假设控制器设计 fi1= fi2= … = fim=0是被排除的，即不会出现所有执行器同时出现故障的情况，则含执行器故障的不确定参数的闭环系统为

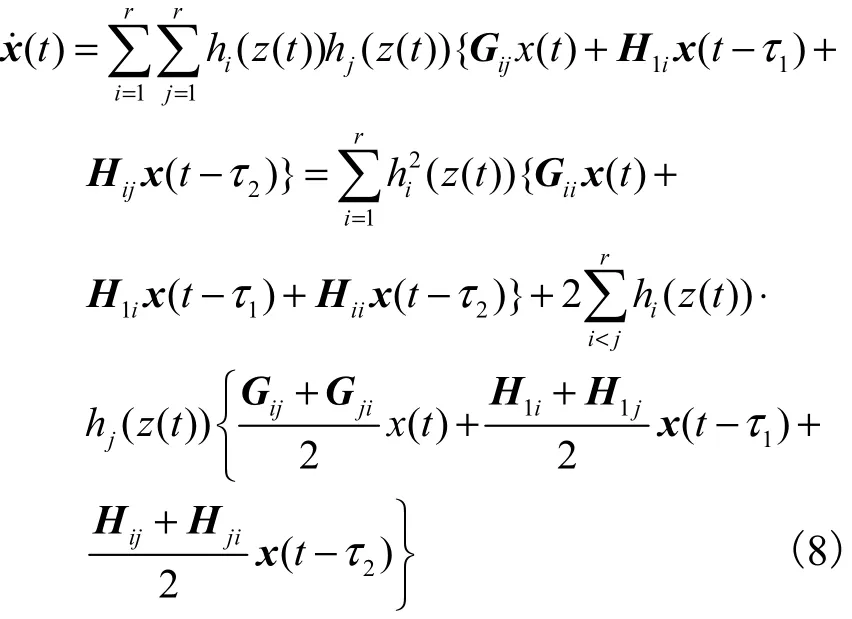
定义 1 对时滞模糊系统式(8)和性能指标式(5)，如果存在控制器式(6)和一个正数 J*，使得对所有允许的不确定性和执行器故障，闭环系统渐近稳定，且性能指标式(5)满足 J ≤J*，则J*称为不确定时滞模糊系统式(8)的一个性能上界，控制器式(6)称为状态反馈容错保性能控制器．

引理 1[17]对于给定的适当维数的任意常数矩阵D、E和对称矩阵S，若

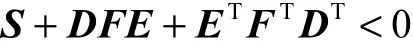
成立，其中T≤FFU，当且仅当存在某一常数0ε＞，有

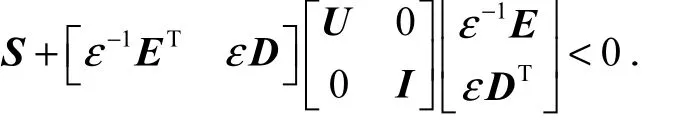
引理2[18]对于任意适当维数的向量x、y和矩阵Y，对任意正定矩阵U，使得

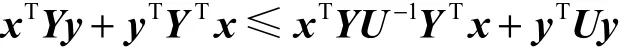
2 容错保成本控制器的设计

本文研究的问题：针对给定的模糊系统式(1)，设计相应的模糊无记忆状态反馈控制器式(7)，使闭环系统式(8)在执行器故障时，仍能保持渐近稳定，同时使性能指标式(5)具有适当的成本上界，进而，优化这个指标使其上界最小化．

首先，给出关于不确定时滞系统式(4)无记忆状态反馈保成本控制律存在的一个充分条件．

定理 1 反馈控制律式(7)是一个保成本控制律，如果对于不确定系统式(8)和一常数σ＞0，存在公共正定矩阵P,U ∈ Rn×n和矩阵 Ki，使得对任意允许的不确定性 Fi( t)，有如下矩阵不等式成立，即

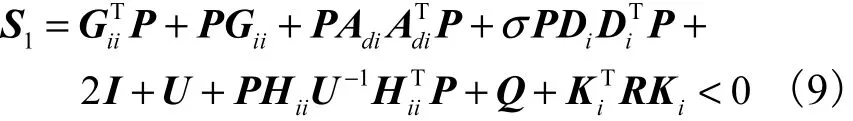
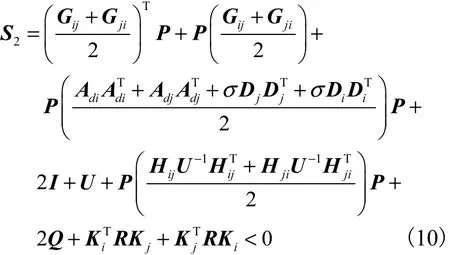
式中1 ≤ i, j≤ r ，且相应的性能指标满足

证明 定义如下准Lyapunov函数

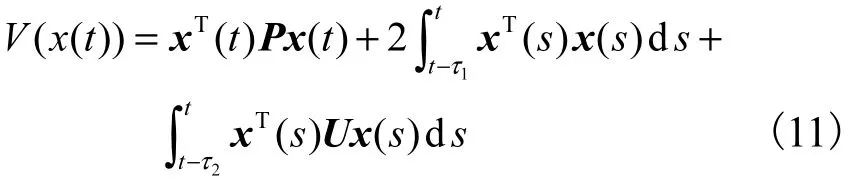
式中，P为对称正定矩阵，U = P2．显然 V (x)＞0,∀x≠ 0 ,则 V (x(t))沿闭环系统式(8)的任意运动轨迹的时间导数为

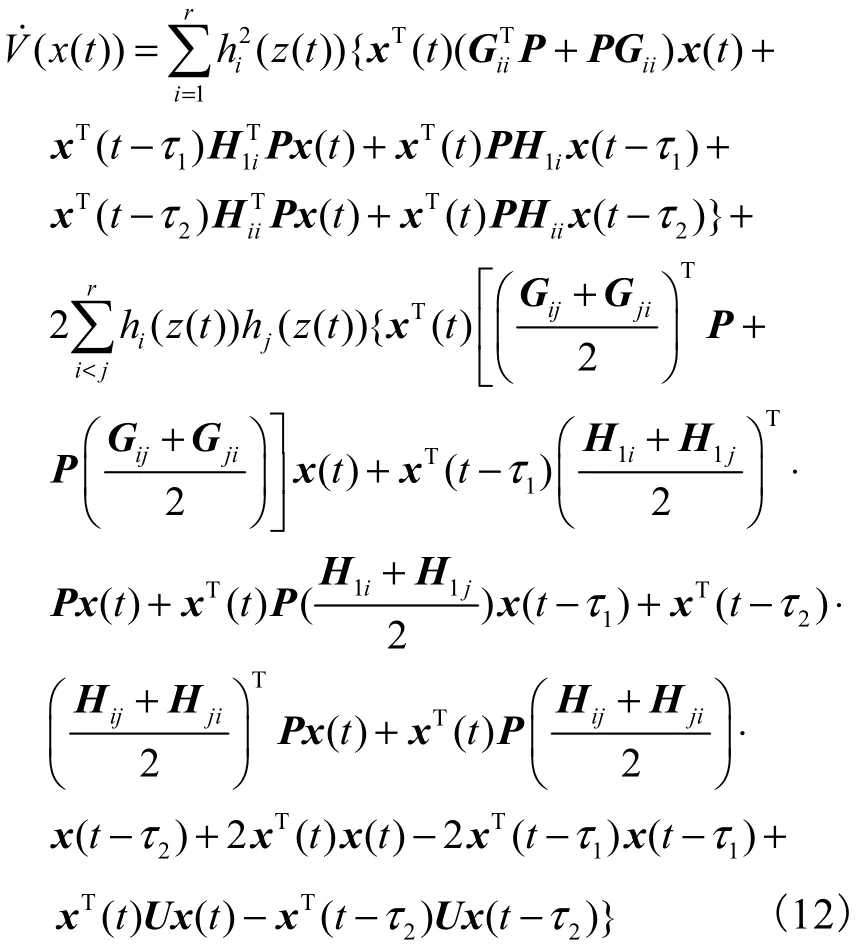
对于任意实矩阵 A，ATA ≤ λmax(ATA)I成立．由假设和引理2，可以得到

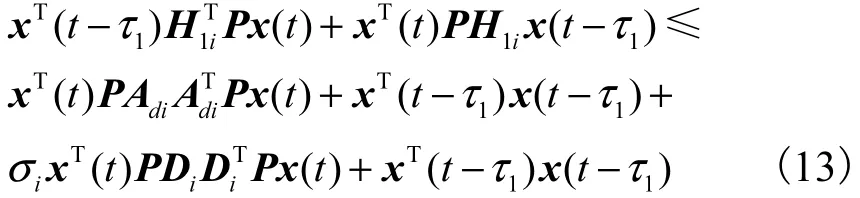
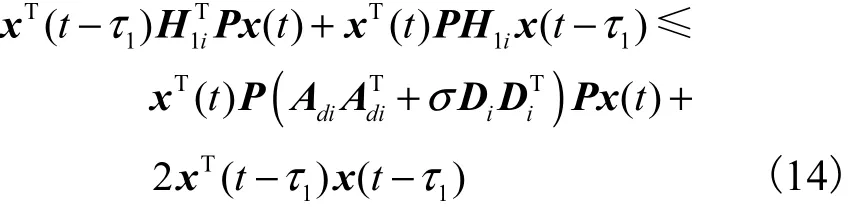
同理可得

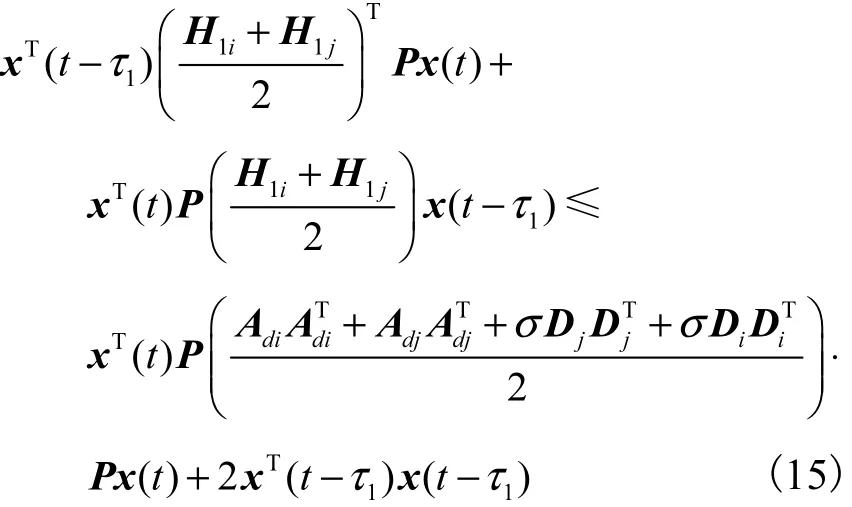
类似地

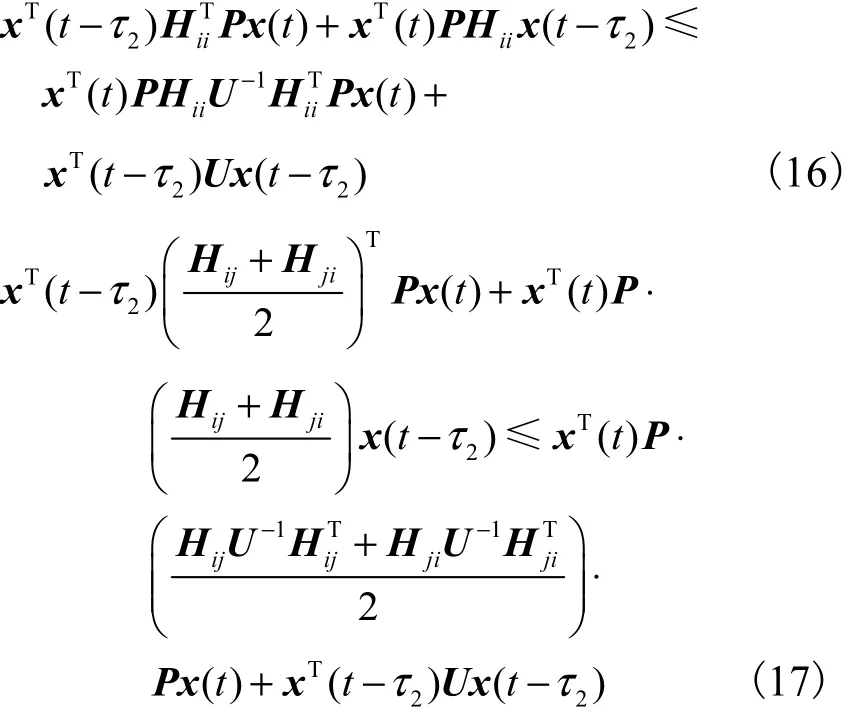
将式(13)～式(17)代入式(12)，得

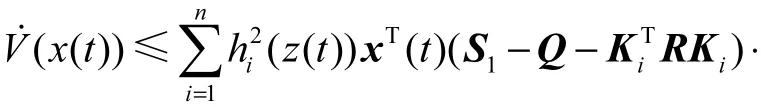
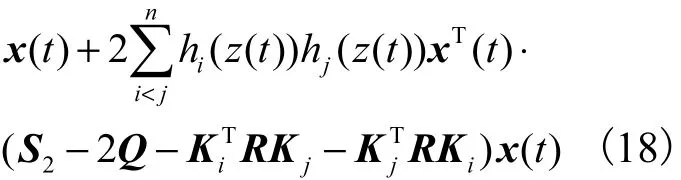
由条件式(9)和式(10)，可得

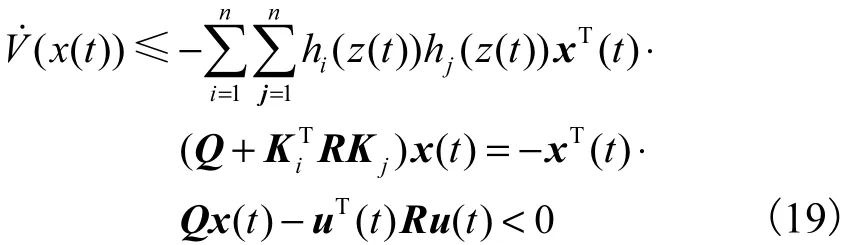
因此，闭环模糊控制系统式(8)是渐近稳定的．进一步利用初始条件式(1)，可得

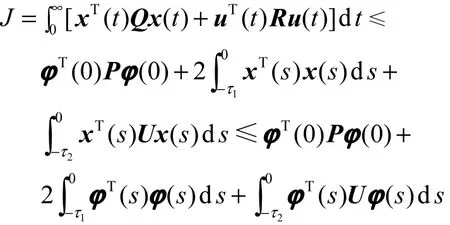
由定义1知，定理1的结论成立．证毕．

由于式(9)和式(10)为非线性矩阵不等式，求解困难，下面给出其LMI的形式．

定理2

(1)存在公共的对称正定阵P和U，使得矩阵不等式(9)和(10)成立，当且仅当存在正数εi，εij(i ＜ j )，矩阵 Wi和公共正定阵X，使得如下线性矩阵不等式成立，即

式中

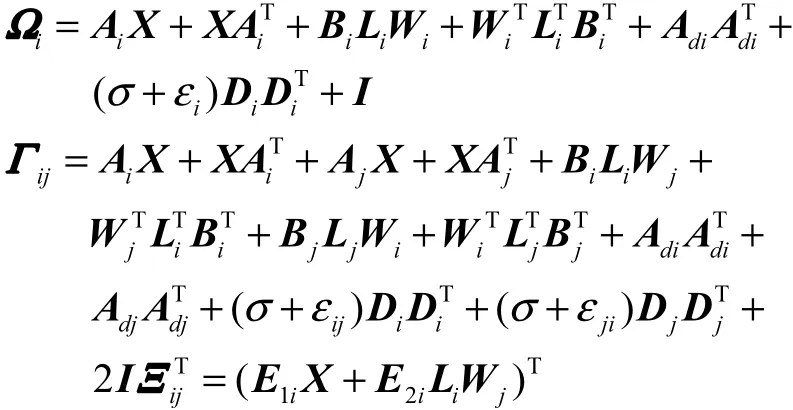
(2)对于系统式(8)，如果线性矩阵不等式(20)、(21)有可行解 εi＞0，εij＞0(i ＜ j)，Wi，X＞0，则无记忆状态反馈控制律

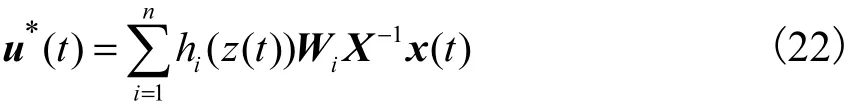
是系统的一个保成本控制律，且

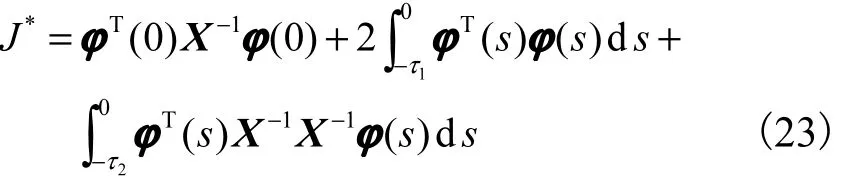
是系统的一个保成本性能指标．

证明 (1)因为

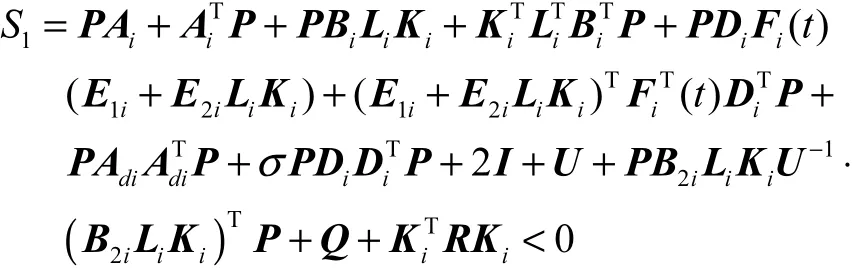
上式两端左右同时乘1−P ，并用引理1，则等价于

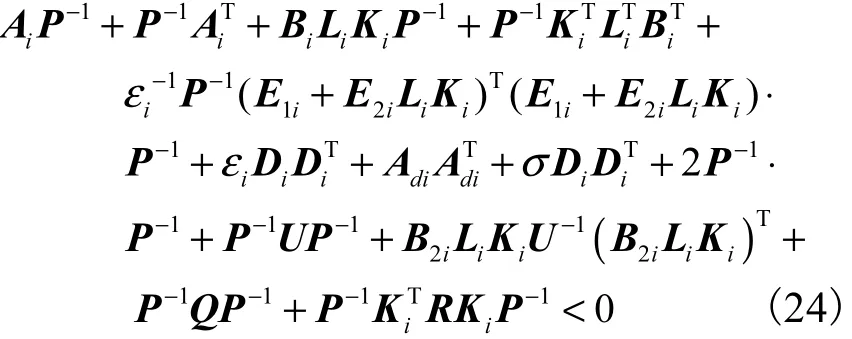
令X = P−1,W =KP−1，则由 Schur补可得式(24)等价

i i于式(20)．同理，式(10)等价于式(21)．

(2)由定理1证明可得．证毕．

定理2提供了一组保性能控制律的参数化表示，这一参数化表示可用来求取使得性能指标值的上界尽可能小的最优保成本控制律．

定理 3 考虑系统式(1)和性能指标式(5)，如果以下优化问题

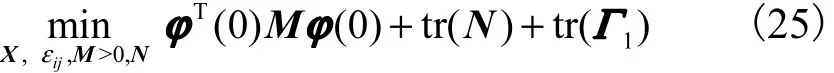
(1) 式(20)和式(21)成立

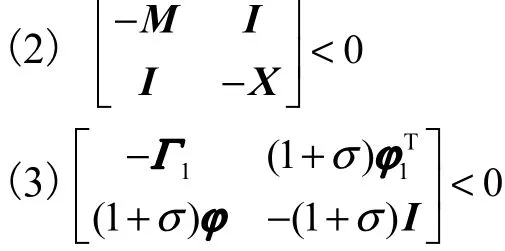
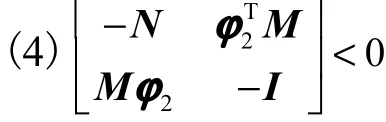
有解 X ,εi, εij( i ＜ j),M ,N ,Γ1，则

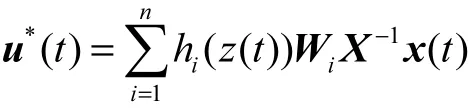
是系统的一个最优保成本控制律．其中

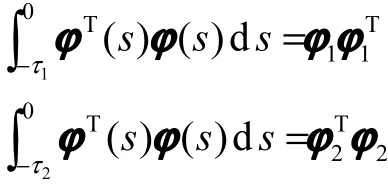
证明 引进M，其中M为对称矩阵，使得1−＜XM，则

同理

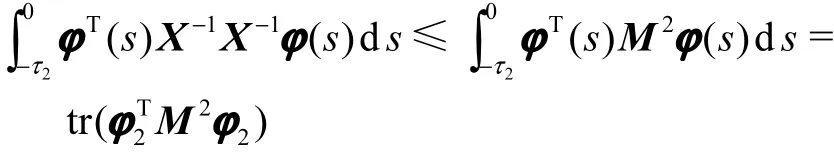
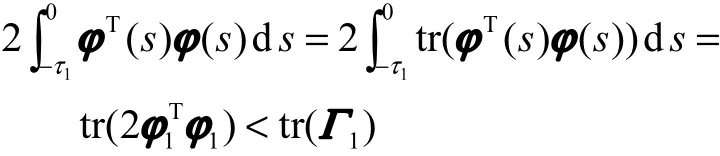
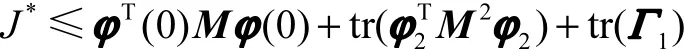
进一步引入矩阵N，使得 ϕ2TM2ϕ2＜ N ，则

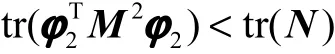
且tr(N)的最小化可以保证 t r(ϕ2TM2ϕ2)的最小化，且可得

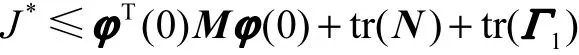
又因为 ϕ2TM2ϕ2＜ N 可等价地表示成线性矩阵不等式，定理得证．证毕．

因为式(25)是一个具有线性矩阵不等式约束的凸优化问题，因此，可以应用凸优化技术来求解该问题的全局最优解．

如果考虑执行器故障但执行器的输出不恒为零的情况，此时，取 fis= αis( 0 ＜ αis＜ 1 )，这时上面结果仍然成立．下一部分故障情况 2即给出了某些故障下αis=0.5时的仿真结果．

3 仿真研究

为了说明控制器的有效性，以文献[19]的非线性系统加控制滞后为例用T-S模糊模型进行描述，即

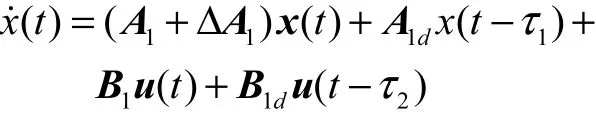
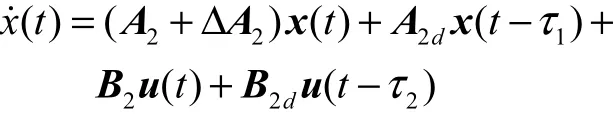
隶属度函数为

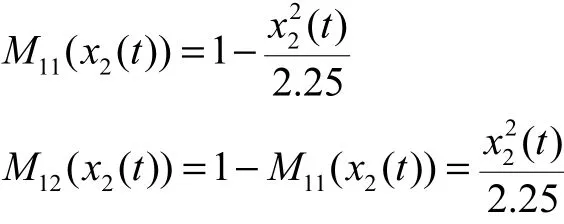
其中

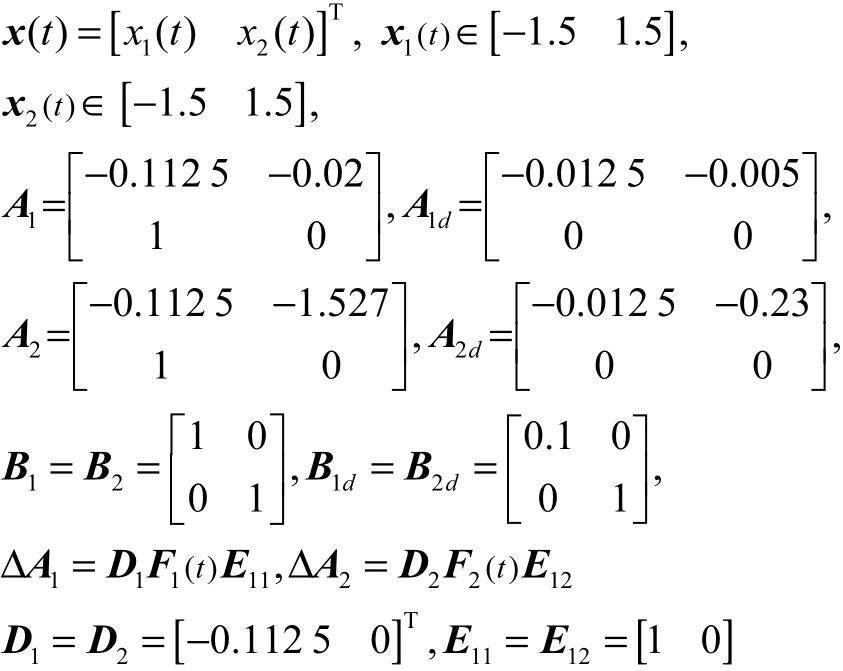
考虑执行器故障分2种情况

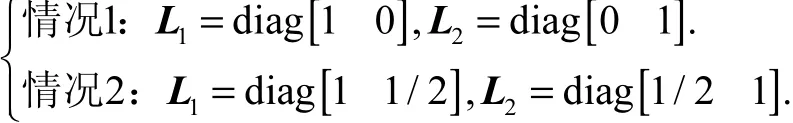
按定理3的 LMIs进行优化，可得到

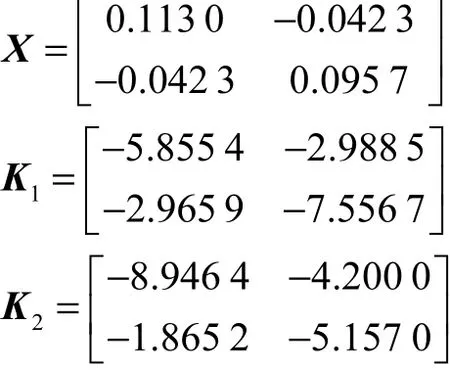
取式(22)的控制律，以初始状态为 x1( 0)=− 1 ,x2(0) = − 1 .2，图 1为系统在执行器无故障时的状态曲线，图2为系统在执行器故障情况1时的状态曲线，图 3为系统在执行器故障情况 2时的状态曲线，如图 1～图 3所示，系统在执行器故障时仍能很快达到稳定，且系统最优性能指标为31.8515= ．

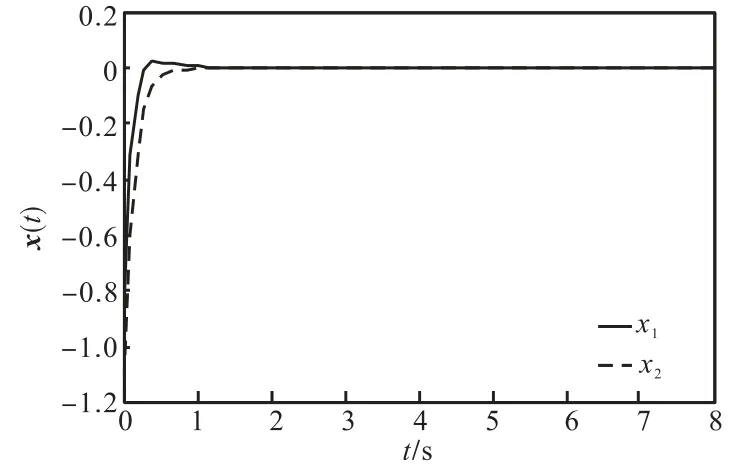
图1 系统正常时状态曲线Fig.1 State curves of system in normal operation

4 结 语

利用模糊 T-S模型对一类不确定非线性时滞系统进行建模，结合一个二次型成本指标，采用线性矩阵不等式的方法，得到系统执行器故障时的保成本容错控制律的一个充分条件．利用求解线性矩阵不等式的方法给出了保成本控制律的设计．最后应用基于LMI的凸优化方法，实现了针对系统故障的最优保成本状态反馈控制器设计．数值算例仿真结果表明，本文提出的保成本容错控制设计方法是有效的．

［1］ 周东华. 叶银忠．现代故障诊断与容错控制[M].北京：清华大学出版社，2000.

Zhou Donghua，Ye Yinzhong. Modern Fault Diagnosis and Fault-Tolerant Control [M]. Beijing：Tsinghua University Press，2000(in Chinese).

［2］ Ackerman J. Parameter space design of robust control systems[J]. IEEE Trans on Automatic Control，1984，20(2)：211-215.

［3］ Shimemura E，Fujita M. A design method for linear state feedback systems possessing integrity based on a solution of a Riccati equation[J]. Int J Control，1985，42(4)：887-899.

［4］ 陈跃鹏，张庆灵，姚 波．广义系统具有完整性的鲁棒二次稳定[J].自动化学报，2002，28(4)：615-619.

Chen Yuepeng，Zhang Qingling，Yao Bo. Robust quadratic stabilization with integrity for descriptor systems[J]. Acta Automatica Sinica，2002，28(4)：615-619(in Chinese).

［5］ 梁 冰，段广仁．基于状态观测器的广义系统鲁棒容错控制[J].吉林大学学报：信息科学版，2004，22(4)：392-396.

Liang Bing，Duan Guangren. Observer-based robust fault-tolerant control for descriptor systems [J]. Journal of Jilin University：Information Science Edition，2004，22(4)：392-396(in Chinese).

［6］ Petersen I R，McFarlane D C. Optimal guaranteed cost control and filtering for uncertain linear systems[J].IEEE Trans on Automatic Control，1994，39(9)：1971-1977.

［7］ Moheimani S O R，Petersen I R. Guaranteed cost control of uncertain systems with a time-multiplied quadratic cost of function：An approach based on linear matrix inequalities [J]. Automatica，1998，34(5)：651-654.

［8］ Guan X P，Lin Z Y，Duan G R. Robust guaranteed cost control for discrete-time uncertain systems with delay[J].IEE Proc Control Theory Appl，1999，146(6)：598-602.

［9］ Yu Li，Chu J. An LMI approach to guaranteed cost control of linear uncertain time-delay systems [J]. Automatica，1999，35(6)：1155-1159.

［10］ Tseng Chwan-Lu，Ko Jung-Yu，Jiang Joe-Air，et al.Guaranteed cost control for uncertain T-S fuzzy systems with time delay[C]// IEEE International Conference on Systems，Man and Cybernetics．Netherlands，2004：2260-2265.

［11］ Guan X P，Chen C L. Delay-dependent guaranteed cost control for T-S fuzzy systems with time delays[J].IEEE Trans on Fuzzy Systems，2004，12(2)：236-249.

［12］ Chen Bing，Liu Xiaoping. Fuzzy guaranteed cost control for nonlinear system with time-varying delay[J].IEEE Trans on Fuzzy Systems，2005，13(2)：238-248.

［13］ Huang Yiqing，Huang Yourui，Tian Yiming. On optimal2H/H∞non-fragile guaranteed cost control for T-S fuzzy system[C]// Proceedings of the 27th Chinese Control Conference. Kunming，China，2008：766-769.

［14］ Wang Xinmei，Pei Hailong，Wu Mei. Robust faulttolerant control studies of state and control time-delay system based on T-S fuzzy model[C]// 2008 International Conference on Intelligent Computation Technology and Automation．Changsha，China，2008：925-930.

［15］ Cao Shuguang，Rees N W，Feng Gang. Analysis and design of fuzzy control systems using dynamic fuzzystate space models[J]. IEEE Trans on Fuzzy Systems，1999，7(2)：192-200.

［16］ Tanaka K，Ikeda T，Wang H O. Robust stabilization of a class of uncertain nonlinear systems via fuzzy control：Quadratic stabilizability，H∞control theory and linear matrix inequalities[J]. IEEE Trans on Fuzzy Systems，1996，4(1)：1-13.

［17］ Lee H J，Park J B，Chen G. Robust fuzzy control of nonlinear system with parametric uncertainties[J]. IEEE Trans on Fuzzy Systems，2001，9(2)：369-379.

［18］ Xu Shengyuan，Lain J. Robust H∞control for uncertain discrete time-delay fuzzy systems via output feedback controllers[J]. IEEE Trans on Fuzzy Systems，2005，13(1)：82-93.

［19］ Lee K R，Kim J H，Jeung E T，et al. Output feedback robust H∞control of uncertain fuzzy dynamic systems with time-varying delay[J]. IEEE Trans on Fuzzy Systems，2000，8(6)：657-663.