土石坝渗流计算中模型尺寸与下游边界条件分析

王建有，郭德霞

（1.郑州大学水利与环境学院，河南 郑州 450001；2.方城县鸭河口灌区管理局，河南 方城 473200）

随着计算机技术的发展，基于有限单元法的渗流分析方法在土石坝的计算分析方面有了广泛的应用[1-6]，在网格剖分和渗透参数一定的条件下，模型尺寸和边界条件成为影响计算结果的主要因素。在模型尺寸方面，文献[4]采用试算法来确定合理的模型尺寸，而在土石坝的下游边界条件方面，则少有文献提及。

1 模型尺寸

在有限单元法中，一个合理模型的建立是至关重要的，在建立渗流计算的模型过程中主要包含4个方面：一是模型尺寸；二是网格剖分；三是介质渗透参数；四是边界条件。模型建立好以后，剩余的就是软件计算问题以及对计算结果的提取和判断问题。

在有限单元法渗流计算过程中，模型尺寸取得越大，坝址附件的计算结果越接近实际情况（如下图1），相应的计算量也在增大。究竟取多大的才能满足实际工程要求，由于不同模型计算条件的复杂性，目前并没有一个明确的说法，有关文献采用试算法来确定合理的模型尺寸。

2 边界条件

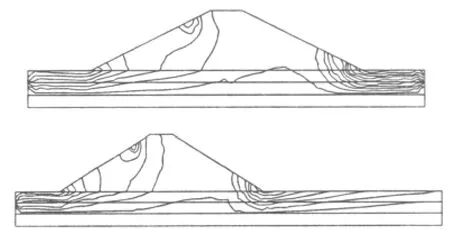
图1 不同模型尺寸情况下的计算结果

在土石坝渗流计算过程中，大部分渗流边界条件是明确的，如河床以上水位线以下部分的水头边界条件（如下图 2 ab，bc，gf，ef）；水位线以上，坝顶以下部分的不透水边界条件 （如下图2 cd）；下游坝顶以下，水面线以上的可能浸出面（如下图2de）。而河床以下部分的边界条件是模糊的（如下图2ah，gi），介于不透水边界和水头边界条件之间。上游边界ah一般取不透水边界，根据上游防渗措施通过延长ab的尺寸来逼近实际情况，这里主要讨论下游边界gi的问题。

图2 土石坝渗流模型

gi边界介于不透水边界和水头边界条件之间，在建立模型的时候，应该尽可能的模拟真实情况，如下游有减压井的情况下取水头边界条件。事实上大多数时候，并不知道下游的真实情况，如下游没有减压井或者水库还没建成的情况，在这种情况下要想准确地模拟下游gi的边界条件是很难的。有些情况下取两种边界条件对大坝的渗流结果影响不大，如下图3，两种边界条件下计算得到的等势线基本一致，最大渗透比降也基本一致。

图3 两种边界条件下计算结果基本一致

有些情况下取两种边界条件对大坝的渗流结果影响很大，如下图4，两种边界条件下计算得到的等势线相差较大，最大渗透比降也相差悬殊。

图4 两种边界条件下计算结果相差悬殊

3 区间检验法

图1计算模型中，坝基第2层的渗透系数较大，模型尺寸对计算结果有较大影响，图3计算模型中，坝基土层渗透系数在1个数量级内，边界条件对计算结果影响较小，图4计算模型中（同图1计算参数），坝基第2层的渗透系数较大，边界条件对计算结果影响较大。

从以上分析可以看出，模型尺寸和边界条件都对计算结果产生影响，且图1、图4的计算条件下，两者都对结果产生较大的影响。为了解决这个问题，提出了区间检验法。

在有限单元法中，边界条件对计算结果的影响是与模型尺寸有关的，模型尺寸越大，边界离中心区域越远，边界条件的变化对中心区域的计算结果影响也越小。对土石坝的渗流计算来说，如果模型尺寸足够大，那么两种边界条件下，坝体附件的渗流计算结果相差不大，当差值小于工程允许的误差范围时，这时候的模型就算合理，两种条件下计算的结果和实际结果的误差也都在允许误差范围之内。

应用区间检验法，图3两种边界条件下，等势线及计算结果都基本一致，说明模型合理。图4两种边界条件下，等势线及计算结果都相去深远，说明模型不合理，需延长模型下游的尺寸，延长至3倍坝高后得到的计算结果如图5，此时等势线及坝体坝脚附近的渗透比降基本一致，说明模型已合理。

图5 延长尺寸后两种边界条件下计算结果基本一致

4 结论

通过对土石坝渗流计算中的模型尺寸以及下游边界条件问题进行了探讨，提出了模型尺寸的区间检验法，解决了模型尺寸及下游边界条件对计算结果的影响问题。

[1]荣冠.三峡工程茅坪溪防护土石坝渗流分析[J].人民长江,2004,35(10):21-23.

[2]张伟,许季军,陈劲松.江口水电站坝址区三维渗流计算分析[J].长江科学院院报,2002,19(2):31-33.

[3]金仁祥.某水库坝基渗透稳定性研究[J].岩土力学,2004,25(1):157-159.

[4]张立杰,杜新强,张立海.哈尔滨市磨盘山水利枢纽区三维渗流数值模拟模型研究[J].吉林大学学报(地球科学版),2003,33(3):327-330.

[5]陆 丽,王瑞骏,李章浩.深厚覆盖层闸坝坝基的三维有限元渗流分析[J].西北水力发电,2006,22(9):9-12.

[6]李宗坤,李彩芳,王建有.燕山水利枢纽土石坝三维渗流分析[J].人民黄河,2008,30(7):92-94.