平行电磁场中锂原子自电离的半经典分析＊

邓善红 高 嵩 李永平 裴云昌 林圣路

(山东师范大学物理与电子科学学院,济南 250014)

平行电磁场中锂原子自电离的半经典分析＊

邓善红 高 嵩 李永平 裴云昌 林圣路†

(山东师范大学物理与电子科学学院,济南 250014)

(2009年6月12日收到;2009年6月24日收到修改稿)

采用包含组合回归的扩展的闭合轨道理论计算了平行电磁场中锂原子依赖于时间的自电离谱,并用半经典的方法解释了电离过程中的混沌现象.讨论了电离电子逃逸时间谱分形结构中隐含的各韵律段的电离轨迹,并得到了轨迹的一般规律,其中特别关注由核散射产生的特殊的逃逸轨迹的性质.具体研究了磁场对锂原子自电离混沌脉冲阵列中电子逃逸轨道和逃逸时间谱的影响.结果发现随着外加磁场的增大,电离脉冲越来越复杂,混沌现象也越明显.这显示了逃逸轨道对初始条件的敏感依赖性.

逃逸轨迹,半经典理论,自电离,核实散射

PACC:0545,0365S,3280D,3260S

1.引言

近年来,超高速扫描照相机斑纹照相术的发展使得高激发态里德堡原子在强场中的鞍点以上自电离的混沌行为越来越引起人们的重视.1996年, Noordam等[1,2]在研究铷原子在外电场中受短脉冲激光激发实验时,发现了里德堡电子波包在Stark鞍点以上自电离衰变的不规则脉冲序列.它不仅提供了一种研究电子波包动力学的新途径,而且开辟了研究混沌输运及粒子从势场逃逸的新领域,成为量子相干控制的典型实例.基于这个实验发现, Mitchell等[3—6]对电磁场中氢原子在鞍点以上自电离做了充分的研究,生动地从理论上重现了Poincaré当年无法定量描绘的有关流形缠绕及同宿栅栏的图像.对于非氢原子,由于原子实的散射作用,在电场中电离就会出现混沌[7],这在Noordam等的开创性实验工作中已经得到证实.而平行电磁场中锂原子的自电离的混沌则是磁场和核散射共同作用的结果[8,9].到达探测器的随时间变化的电离电子流通量可以看做是由短脉冲激光激发的价电子从核和外场中逃逸而形成的.关于电离电子脉冲阵列对于时间的依赖性以及(冰柱状)电离碎片初始出射角分布等,已有较多探讨[3—5].但对于不同出射角度的电子的逃逸轨迹怎样开始进入自电离通道?磁场对自电离混沌性质及电子轨道有什么影响?就我们所知,这些问题还没有人研究.本文用扩展的半经典闭合轨道理论计算了自电离电子流通量[10],给出了依赖于时间和初始出射角度的电离电子逃逸谱,显示了一种无穷嵌套的韵律性自相似结构[11,12],具体讨论了核散射对电离脉冲的影响,详细研究了各韵律段落中电离电子轨迹的规律性.并计算了不同磁场下自电离谱及电子逃逸轨迹的变化.

2.标度变换及体系哈密顿量

平行电磁场中锂原子的哈密顿量在柱坐标中可表示为

这里已假定电、磁场沿对称轴方向.其中,f= F/(5.14×109V/cm),F为电场,a=1/2.13为可调参数[13],势函数中的Z表示原子的核电荷数.为了使量子和经典对应,对上述各个量进行标度变换[14,15]变换后的哈密顿量为

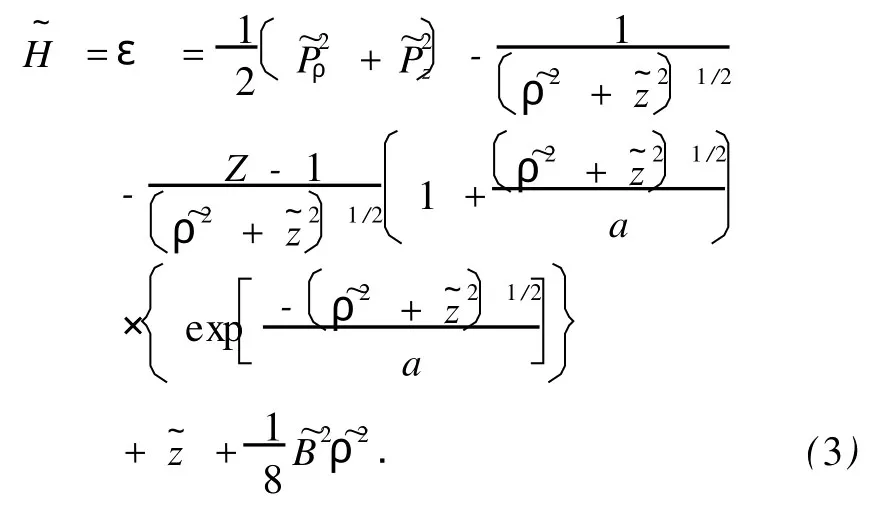
需要说明的是,对存在模型势情况,上述标度律一般不成立,这是因为指数项模型势是短程势,而在近核区,外电场作用可忽略,无法对力学量进行标度.但考虑到电离通量所关注的是远离核的情况,除了非常靠近核的极小区域,(3)式仍是好的近似.此外,为了消除库仑势中的奇异性,变换到半抛物坐标[3]

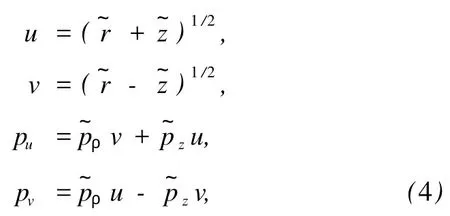
并引入有效哈密顿量标记h=2r～(~H-ε),则

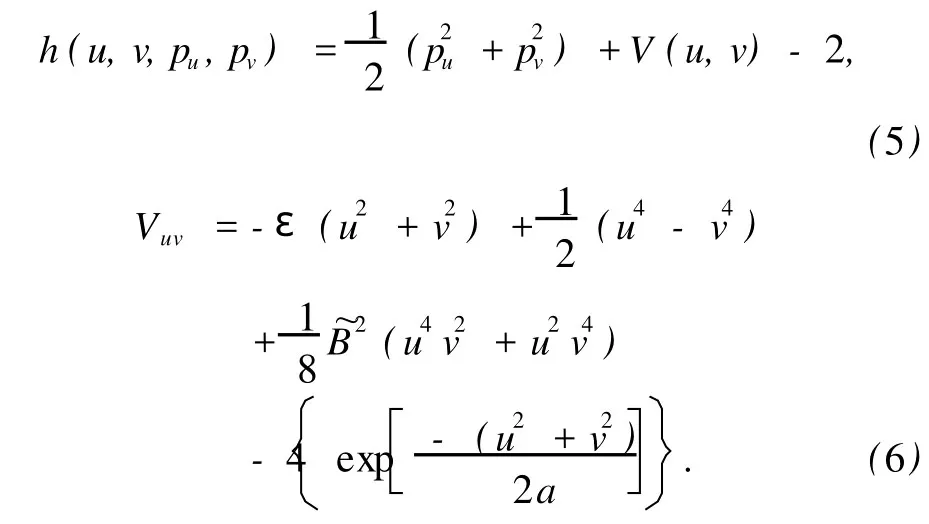
采用包括势散射的扩展的闭合轨道理论方法可以计算外场中原子自电离电子流到达探测器的通量.图1为标度能ε=-1.3,标度磁场B=4.5时锂原子在平行电磁场中的电离率谱,这种逃逸时间图具体展示了电离电子流通量对时间和电子初始出射角的依赖关系.谱的时间分辨率为皮秒(ps)量级.

3.自电离的半经典解释以及不同出射角电子轨迹的研究

自电离过程可以用半经典的方法解释:当一束短脉冲激光打到置于平行电磁场中(沿z轴方向)的锂原子上,价电子吸收光子,产生从原子实向各个方向出射的具有固定标度能量的电子波包.在远离核处,这些电子波包在库仑场和外场联合作用下,沿经典轨道传播.一些沿着探测器的方向的被电场加速后直接向下的电子轨道产生最先看到的即时脉冲.沿着向上方向的电子轨道,在外场的作用下将返回核附近,由于核散射的作用,这些返回的电子波包将被散射到各个方向,其中有一部分将会打在探测器上形成第二个电子脉冲,而那些沿其他方向散射的电子轨道将在场的作用下经过更多次核散射,最终达到探测器产生电子脉冲,从而产生一系列的混沌电子脉冲阵列(见图1(a)).电子打到探测器上的时间(逃逸时间)与电子轨道的初始出射角θ(出射方向与z轴的夹角)有密切的关系,如图1(b)所示,出射角度在一个小范围内的电离电子在沿探测方向上的速度分量不同,它们到达探测器的时间有先后,通量强度也不同,因而形成一个有一定宽度而且高度略有起伏的类似冰柱状图形的电离碎片,每个冰柱对应于一个脉冲,并且每个冰柱有两个临界角,表示初始出射角处在这两个角度范围内,电子轨道将会发生电离(逃逸).当出射角接近该临界值时,逃逸时间趋向无穷.

以下研究在(ρ,z)坐标中电子的电离轨道.电磁场中的锂原子的势能面有个无限深的库仑势阱,在静电场的作用下,势阱将一边被抬高,一边被压低并形成势能鞍点.电离轨迹开始于原子核附近,在库仑势阱中经历混沌的振荡,最终电子越过鞍点区域进入电离通道,打到位于z=-4的探测器上,形成电离脉冲.对于向探测器方向入射的电子,不经过核散射作用而直接电离,我们将这部分电子轨道称为“直接部分”的电子轨道.图2为初始出射角度分别为137.3952°,129.0310°,127.5970°, 127.3112°时直接部分的电子轨道,它们开始于原子核附近,当出射角度很大时电子在ρ方向上不发生振荡,在电场的作用下直接越过势能鞍点打在探测器上,这里相应于初始出射角为137.3952°.随着角度的减小,逃逸的电子轨道在ρ方向上发生振荡,角度越靠近冰柱的临界角,轨道在ρ方向的震荡次数越多.当出射角度达到冰柱的临界值时,电子轨道将会在鞍点区域附近进行无数次的振荡,永远不会发生逃逸,即不发生自电离.在连续逃逸时间图中,每个冰柱的尖端部分发生逃逸的时间最短,随着角度接近冰柱的临界角,逃逸时间趋向无穷.逃逸电子轨迹都将遵循这个规律.

图1 锂原子的电离概率及碎片冰柱图 (a)锂原子在电场强度为19 V/cm,磁场强度为4.5,主量子数为80,标度能为-1.3的电离概率图;(b)锂原子在相同条件下做出标度后的电离时间随初始出射角度变化冰柱图;(c)与(b)相对应的精度较高的逃逸时间图

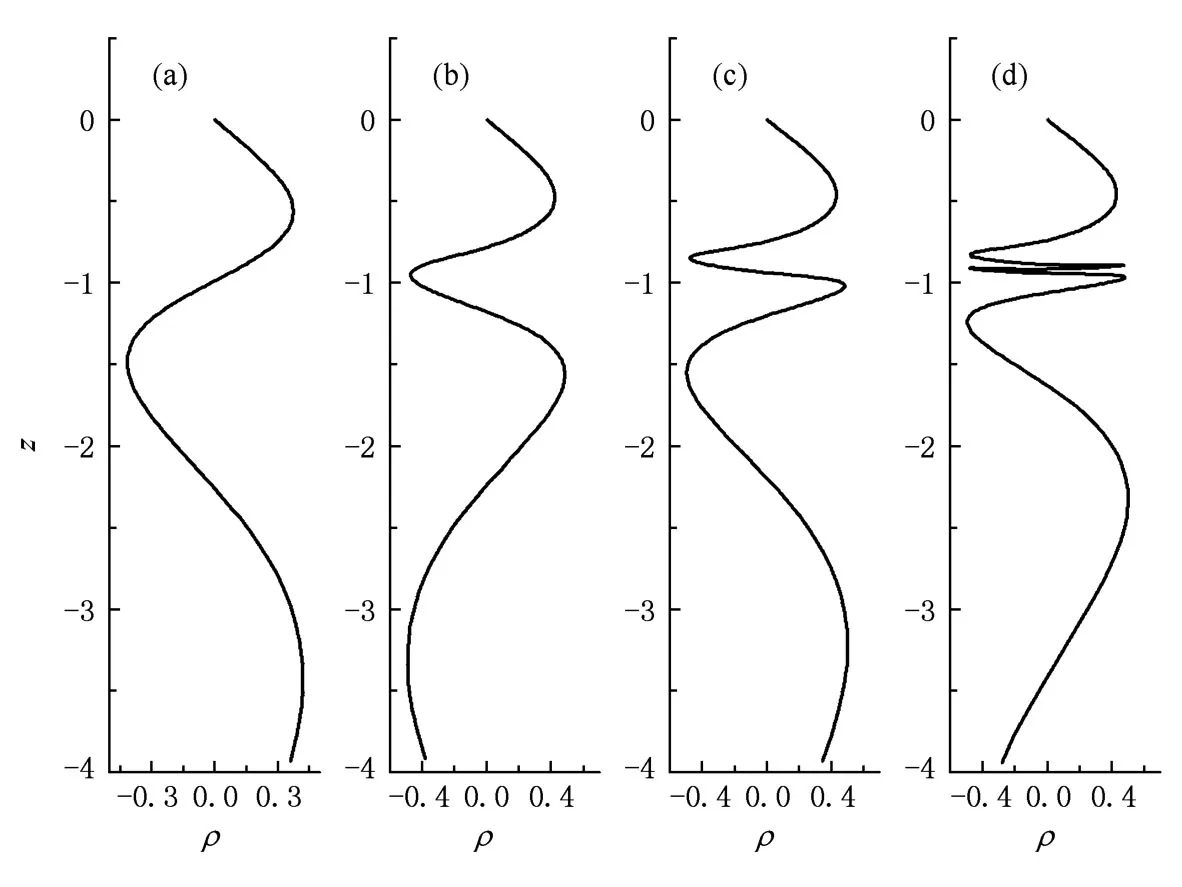
图2 “直接部分”中不同电子初始出射角时的电子逃逸轨道及其振荡行为(a)θ=137.3952°,(b)θ=129.0310°,(c)θ=127.5970°,(d)θ=127.3112°

同一个冰柱上的轨迹存在上述规律,不同的冰柱间的电子轨道也具有一定的规律性.图3为平行电磁场中锂原子F=19 V/cm,B=4.5的电子连续逃逸轨道图,展示了自相似结构,并且具有一定的韵律性[8].图中(a)—(d)为同一类韵律段A,(e)—(h)和(i)—(l)为另外两类韵律段B,C,每个段落中各部分具有相似的结构,其相应电离碎片位置可参看图1(c).例如:(a)和(b),(c),(d)具有相同结构,这种相似性在电离电子轨道中也有所体现.为了便于比较,选择冰柱的尖端部分进行研究,如图3所示A韵律的电子轨道均从核附近出发,(a)尖端的电子轨道绕核一周后发生逃逸,(b)将会在鞍点区域附近发生振荡后再绕核一周,然后发生逃逸,而韵律中(c)和(d)的轨道将会在鞍点附近经历更多的振荡.B韵律的轨迹绕核两周后发生逃逸,韵律开始时(e)的轨迹在鞍点附近振荡得比较小,随后(f),(g),(h)在鞍点附近振荡得越来越剧烈.对于C韵律也同样存在这样的规律.A,B和C韵律的冰柱尖端的电子轨迹产生这种规律是由于模型势和库仑势共同作用的结果,当然,在外部区域则是外加电磁场和库仑场对电子轨道的折转.平行电磁场中的氢原子,由于电子在核附近只有纯库仑散射而没有核散射,其相应电子轨迹略为简单,谱的韵律结构有所不同[5].电磁场中的锂原子存在原子实的核散射作用,但缺少了磁场对电子轨道的回旋作用,使得逃逸时间图中存在一些不同的尖锐的冰柱,这些冰柱的尖端的逃逸轨道如图3(m)—(p)所示,与A,B,C韵律电子轨迹不同的是,这些特殊的轨道由核附近出发,然后再回到核附近,在核散射作用下,由核出发经外电场加速直接达到探测器上,而没有在外磁场中回旋部分,这是直观图像.总之,平行电磁场中锂原子的电离混沌脉冲是由于核散射和磁场共同作用的结果.

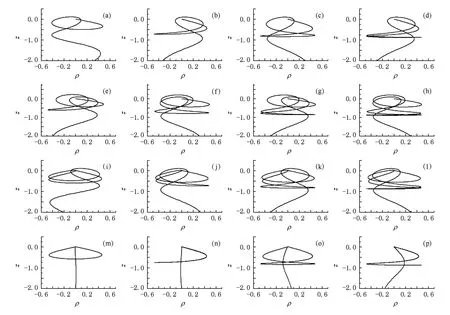
图3 平行电磁场中锂原子的电子连续逃逸轨道图及单独由核散射作用引起的电子逃逸轨道图 (a)—(d)为同一类韵律段落,(e)—(h),(i)—(l)为另两类韵律段落,(m)—(p)为特殊的尖锐冰柱尖端的电子轨道

4.磁场对锂原子自电离混沌脉冲及其电子轨道的影响

磁场是产生锂原子混沌脉冲的原因之一,通过改变磁场强度可以对混沌脉冲产生显著影响.平行电磁场中锂原子鞍点能为ε=-2,发生自电离标度能需要满足大于鞍点能,仍取标度能ε=-1.3,固定电场强度F=19 V/cm,改变磁场强度.考察B= 2.5,3.5,4.5,5.5时,锂原子的逃逸时间图以及在不同磁场引起出射角度为103.91°时电子逃逸轨道的变化.图4给出了数值模拟的结果.

比较不同磁场下的逃逸时间图发现随着磁场强度的增大,冰柱的数量逐渐增多;各个冰柱最短逃逸时间(尖端部分的电子轨道逃逸时间)逐渐减小;“直接部分”的角度范围也逐渐减小;而最早达到探测器上的“直接部分”电子的逃逸时间逐渐增大.直观地可以这样解释:由于电子受到电场、模型势、库仑场以及磁场的共同作用,电子受电场的作用向下运动,而库仑吸引力和磁场增加了它向核的方向运动.当磁场相对较小时,电子受到的回旋作用比较小,使得“直接部分”的电子轨道在大角度范围内不能再次回到核附近而是直接打到探测器上.磁场增强时,电子受到的回旋作用增大,所以最早达到探测器上的“直接部分”电子的逃逸时间逐渐增大.另一方面,当磁场强度增大时,由于回旋运动增加了出射电子返回核附近的可能,因而增加了电离碎片数,与其对应的混沌电离脉冲会越来越复杂,体系的混沌现象越来越明显.图4(a)—(d)表示外加磁场强度依次增大时,相应地依赖于时间的自电离率的变化.显然,随着磁场的增大,自电离谱发生显著变化,其混沌特征越来越突出.图4(b), (e)—(h)显示了在相应外加磁场下一个特定的初始出射角度为103.91°时的电子逃逸轨道变化.可以看出,电子运动的轨迹对于磁场的变化是十分敏感的:当磁场B=2.5时,电子绕核一周后发生逃逸;当磁场强度增为3.5时电子绕核两周后逃逸.磁场越强,电离电子逃逸前绕核的次数越多,轨道越复杂.

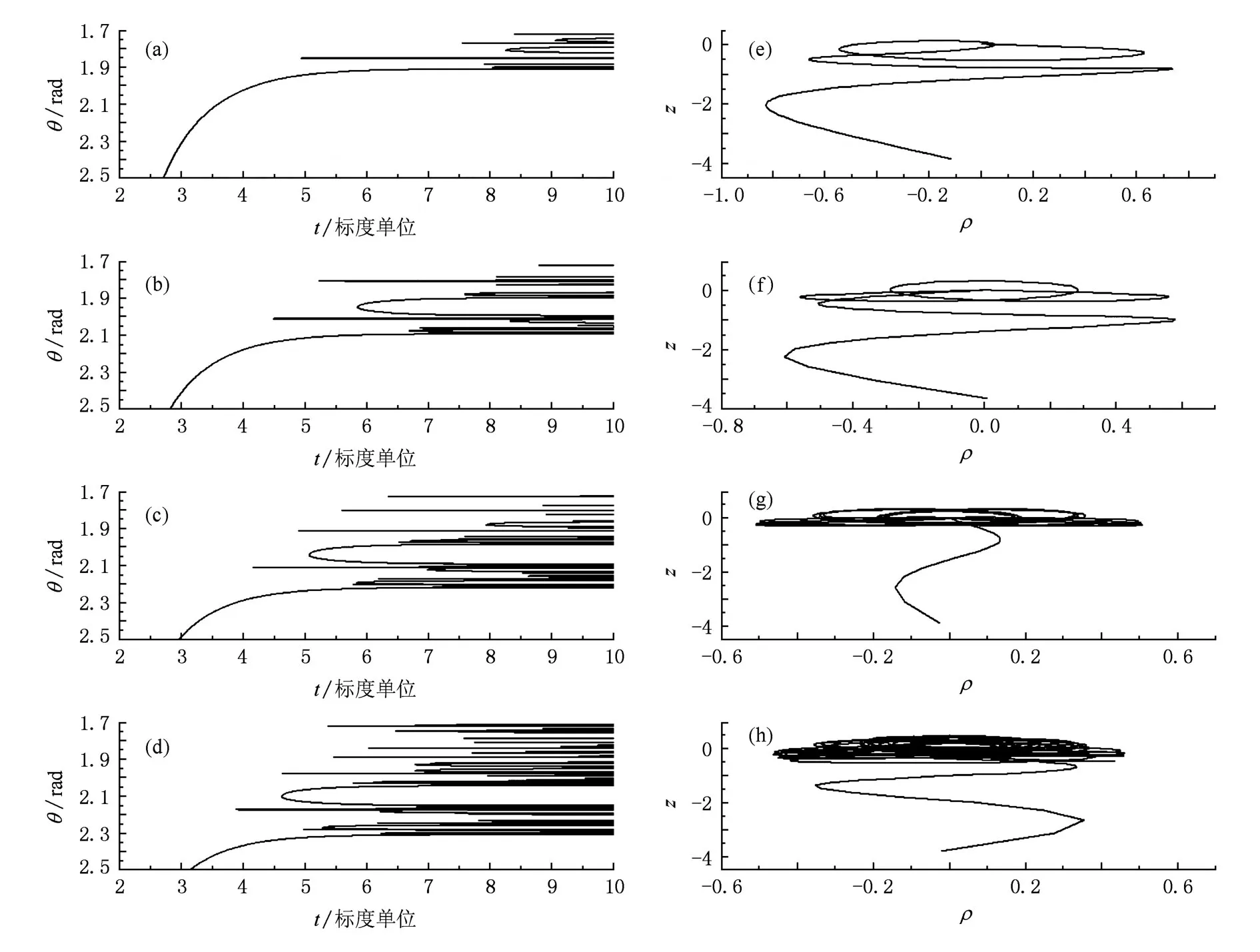
图4 标度能ε=-1.3,电场F=19 V/cm,不同磁场强度的电子逃逸时间图及电子出射角度为103.91°时的逃逸轨道 (a)—(d)为B=2.5,3.5,4.5和5.5时的电子逃逸时间图;(e)—(h)为θ=103.91°,B=2.5,3.5,4.5和5.5时的逃逸轨道图

5.结 论

用半经典的方法计算得到了平行电磁场中高里德堡锂原子在鞍点以上的自电离逃逸时间图(自电离碎片-冰柱图)及其对电子初始出射角的依赖关系;用直观的电子电离轨道图像解释了电离过程的混沌现象;寻求自相似结构在电子轨道上的规律性特征.首先,同一个冰柱中不同出射角电子轨迹将会在鞍点附近ρ方向上发生多次振荡.而当角度趋向于临界值时,电子轨道无限振荡,逃逸时间就变成无穷,电离过程截止.其次,不同自电离碎片之间存在一定的“韵律性”,A,B,C为三个典型的韵律,韵律中的每一部分均具有自相似性,表现在电子轨道的形状上则可以按电子电离轨道绕核圈数加以区分.离子实散射作用和磁场的回旋效应是体系产生混沌电离脉冲的根本原因:由于离子实的核散射作用,当电子回到核附近经历了一次或多次核散射后发生电离.核散射的方向、角度的完全无规律性导致了电离谱的混沌.而磁场的回旋效应极大丰富了电子轨道的形式,随着磁场的增强,体系的电离混沌脉冲越来越复杂;磁场对某一特定出射角的电子轨道的影响也是十分显著的.这表明,自电离动力学特性敏感地依赖于初始条件,因而从本质上看,它是混沌的.我们的研究有助于直观理解非氢原子在强外场中自电离过程的混沌现象.

[1]Lankhuijzen GM,Noordam L D 1995Phys.Rev.A 52 2016

[2]Lankhuijzen GM,Noordam L D 1996Phys.Rev.Lett.76 1748

[3]Mitchell K A,Handley J P,Tighe B,Delos J B 2004Phys. Rev.Lett.92 073001

[4]Mitchell K A,Handley J P,Tighe B,Delos J B 2004Phys. Rev.A 70 043407

[5]Mitchell KA,Delos J B 2007Phys.D 229 9

[6]WangD H,Huang K Y,Zhou H,Lin S L 2009J.Electron Spectrosc.Rel.Phenom.169 86

[7]Zhou H,Li H Y,Gao S,Zhang Y H,Jia ZM,Lin S L 2008 Chin.Phys.17 4428

[8]Lin SL,Zhou H,Xu X Y,Jia Z M,Deng S H 2008Chin. Phys.Lett.25 4251

[9]Gao S,Xu X Y,Zhou H,Zhang Y H,Lin SL 2009Acta Phys. Sin.58 1473(in Chinese)[高 嵩、徐学友、周 慧、张延惠、林圣路2009物理学报58 1473]

[10]Dando P A,Monteiro T S,Delande D,Taylor K T 1996Phys. Rev.A 54 127

[11]Mitchell KA,Handley J P,Tighe B,Delos J B 2003Chaos13 880

[12]Mitchell KA,Handley J P,Tighe B,Delos J B 2003Chaos13 892

[13]CourtneyM,Spellmeyer N,Jiao H,Kleppner D 1995Phys. Rev.A 51 3604

[14]Gao J,Delos J B,BaruchM 1992Phys.Rev.A 46 1449

[15]HaggertyM R,Delos J B 2000Phys.Rev.A 61 053406

PACC:0545,0365S,3280D,3260S

A sem iclassical analyses on the auto-ionization of lithium atom in parallel electric and magnetic fields＊

Deng Shan-Hong Gao Song Li Yong-Ping Pei Yun-Chang Lin Sheng-Lu†

(College of Physics and Electronics,Shandong Nor mal University,Jinan 250014,China)

12 June 2009;revised manuscript

24 June 2009)

Based on the extended closed-orbit theorywith the combination recurrence induced by the nuclear core scattering,we calculate the time-dependent auto-ionization rate of lithium atoms in parallel electric and magnetic fields,and the chaotic behavior in the auto-ionization process is explained.A qualitative description of the shape of the ionizing trajectories from the nesting distinct fractal epistrophes is given.In particular,some special escape trajectories induced by core-scattering is obtained in configuration space.The escape time and the auto-ionization rate that exhibit a series of chaotic pulse train are discussed for different magnetic fields.We find that,with the increase of the magnetic field,the ionizing electron pulse train along with the corresponding ionized electron trajectories become more and more complicated,showing the sensitive dependence of the dynamic properties on the initial conditions.

escape trajectories,semi-classical theory,auto-ionization,core scattering

＊国家自然科学基金(批准号:10774093,10374061)资助的课题.

†通讯联系人.E-mail:sllin@sdnu.edu.cn

＊Project supported by the NationalNatural Science Foundation of China(GrantNos.10774093,10374061).

†Corresponding author.E-mail:sllin@sdnu.edu.cn