半导体/磁性d波超导隧道结中的散粒噪声
梁志鹏 董正超
1)(苏州大学物理科学与技术学院,苏州 215006)
2)(淮阴师范学院物理系,淮安 223001)
半导体/磁性d波超导隧道结中的散粒噪声
梁志鹏1)2)董正超2)†
1)(苏州大学物理科学与技术学院,苏州 215006)
2)(淮阴师范学院物理系,淮安 223001)
(2009年3月23日收到;2009年6月17日收到修改稿)
考虑到磁性d波超导体中的能隙与磁交换能的依赖关系,通过求解Bogoliubov-de Gennes(BdG)方程,利用Blonder-Tinkham-Klapwijk理论方法研究半导体/磁性d波超导隧道结中的散粒噪声.计算结果表明:磁性d波超导结中的磁交换能h0可导致散粒噪声在零偏压处的双峰和能隙处的峰出现劈裂,劈裂的宽度为2h0;磁交换能h0同时对散粒噪声及噪声功率与平均电流的比值有抑制作用.
磁性d波超导体,半导体,散粒噪声
PACC:7475,7450
1.引言
在准粒子输运过程中,载流子的离散特性可引起散粒噪声.散粒噪声为依赖于时间的电流围绕其平均电流有一涨落.研究隧道结系统中的散粒噪声可以获得一些有关准粒子传播的重要信息,而这些信息通常又不能在测量隧道谱或测量系统电阻率中获得.另一方面,在诸多器件中,如存在散粒噪声,对测量信号会产生影响,降低或消除系统的散粒噪声能提高测量的信号的精度.在激光器件中,通常通过串联一个很大的电阻于发射源上以降低散粒噪声,这样可以获取单色性较好的激光源.过去几年中,人们对介观系统中的散粒噪声[1—3],尤其是正常金属/超导隧道结中的散粒噪声已做了深入系统的研究[4—7].研究结果表明,在较低偏压下, Andreev反射[8]以及Cooper对的电荷输运会明显地影响系统中的电流涨落.另外,超导体中配对势的对称机理对散粒噪声也将起重要作用.对于正常金属/s波超导隧道结[4,5],在隧道极限下,散粒噪声功率与平均电流的比值在零偏压处为4e(e为单电子电荷量),而当加偏压大于Δ0/e(Δ0为超导的能隙)时,其比值为2e,即过渡到经典的Schottky[9]值.这个特征可解释为:当一个电子以小于超导能隙的能量从正常金属入射到系统结中时,将反射一个空穴,从而导致以2e电荷的Cooper对流进超导体中;而当一个入射电子能量大于超导能隙时,穿透到超导体中的准粒子所带电荷为e.对于正常金属/d波超导隧道结而言,散粒噪声功率与平均电流的比值在零偏压处为零,在较大偏压处为2e,这一奇异行为归结为在正常金属/d波超导界面处有零能束缚态形成.
近来人们对一些新型磁性材料的研究产生了极大兴趣,其中引人关注的就是人们在大块CeCoIn5[10—12],UGe2[13],ZrZn2[14],URhGe[15]等磁性材料中观测到了超导性.研究表明:CeCoIn5具有自旋单态的d波超导特征[16—18],然而对于UGe2, ZrZn2,URhGe,有关其电子配对的对称性问题目前仍处于争议中.虽然有些研究者认为这些材料的超导性具有s波配对特征[19—21],但是考虑磁交换能的拆对效应,又有人认为自旋三重态配对更为合理[22—24].尽管目前已有很多有关正常金属/超导隧道结[6,7,25]、铁磁/超导隧道结[26—30]中散粒噪声的研究报道,但有关半导体/磁性d波超导隧道结中的散粒噪声的研究报道很少.
本文通过求解磁性d波超导体中的能隙与磁交换能的自洽方程,考虑GaAs中两种不同空穴载流子(即重空穴与轻空穴)输运和磁性d波超导体不同晶轴取向,在隧道极限下,研究磁性d波超导体中的磁交换能对半导体/磁性d波超导隧道结中的散粒噪声的影响.
2.半导体/磁性d波超导隧道结中的准粒子输运系数的计算
在磁性d波超导体中,超导体的能隙与温度及其内部的磁交换能有关.利用平均场近似的方法可推导出磁性d波超导体的自洽能隙方程为[31,32]
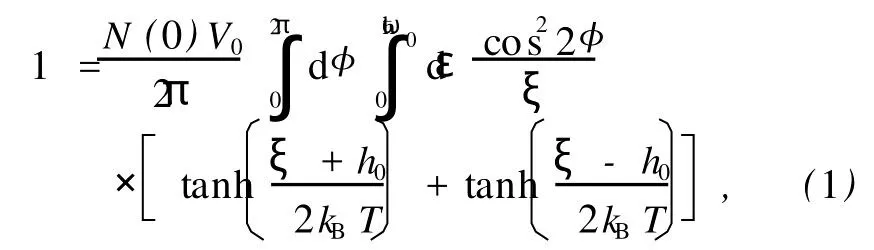

其中θS是准粒子入射方向与x轴方向的夹角,α是d波超导体的a晶轴方向与x轴方向的夹角,Δ+, Δ-分别对应于d波超导体中电子型和空穴型的配对势.为了讨论方便,我们假设所构建的隧道结为二维隧道结,半导体与超导体的界面位于x=0处,界面散射势垒的宽度忽略不计,其散射势为U= U0δ(x),设界面处无粗糙散射.运用Bogoliubov-de Gennes(BdG)[33]方法计算该隧道结中的准粒子输运系数.在模型中没有考虑准粒子自旋反转的情况,自旋依赖于四分量的BdG方程可分解为两个独立的二分量方程分别描述Cooper对中电子型和空穴型准粒子不同的自旋方向,其形式为(u↑,v↓)和(u↓,v↑),BdG方程可表示为

在半导体GaAs中,其多数载流子是空穴.图1表示一空穴以角θ从左边半导体入射到系统隧道结中的准粒子示意图,其中b是正常反射空穴,a是Andreev反射[8],cσ和dσ—分别表示穿透到右边磁性超导体中的空穴型和电子型准粒子.通过求解(3)

图1 半导体/磁性d波超导隧道结准粒子传播示意图
式可得空间准粒子的波函数如下:

式中,qh,qe,k-σ和k+σ—分别为各散射粒子的波矢值,有
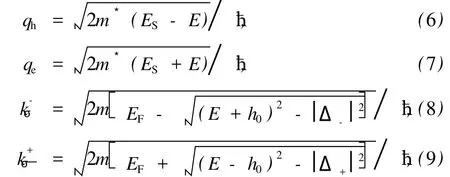
式中,m*为半导体中空穴载流子的有效质量,ES为半导体的费米能,ħ=h/2π,其中h为普朗克常数.在超导体一侧准粒子波函数的表达式中,超导体内的相干因子为

相位因子为

利用边界条件


3.半导体/磁性d波超导隧道结中散粒噪声和噪声功率的计算
Blonder-Tinkham-Klapwijk(BTK)[34]理论给出了正常金属/s波超导隧道结电导和电流的计算公式.有了以上所得的a,b系数,利用文献[5,6]用于计算正常金属/超导隧道结中的散粒噪声公式,可推广到半导体/磁性d波超导隧道结系统,在零温下,散粒噪声可表示为

其中

对散粒噪声在能量区间0—eu上积分,即可得0 K时的噪声功率为

式中u为偏压.另外,利用平均电流公式

这儿的G是微分电导,

其中

由此可以计算反映系统内载流子携带基本电荷信息的噪声功率与电流的比值.
下面利用(18)—(23)式并结合(1)式数值计算半导体/磁性d波超导隧道结系统的散粒噪声、噪声功率与平均电流的比值,在取不同磁交换能h0/Δ0下随偏压u的变化关系.
图2表示半导体载流子为重空穴时,在磁性d波超导体内的磁交换能h0取值不同时,散粒噪声与加在半导体/磁性d波超导隧道结上的偏压的变化关系,其中图2(a)对应磁性d波超导体的晶轴方位角α=0时的情况,图2(b)对应晶轴方位角α=π/ 4时的情况,图3为相应噪声功率与平均电流的比值的曲线.从图2可以看出,对于h0=0,图2(a)中散粒噪声在能隙处存在能隙峰,图2(b)中由于在界面处存在中间束缚态,在u=0处Andreev反射系数并随着偏压的增加而迅速减小为零. Andreev反射系数在很窄的偏压区的明显变化,导致散粒噪声在零偏压处形成一个很窄的双峰结构[5],其中一个峰位于u>0,另一个峰位于u<0.随着磁交换能h0的存在图2(a)中能隙处的峰劈裂为两个子峰,图2(b)中的双峰也被劈裂,劈裂的宽度为2h0.从图2还可以发现,随着磁交换能的增大,劈裂的峰值被压低.在图3中,当超导体内无磁交换能时,噪声功率与平均电流的比值的曲线与正常金属/d波超导隧道结的结果类似[7];当存在超导磁交换能时,对于α=0,噪声功率与平均电流的比值的曲线随着交换能的增加明显地被压制;在α= π/4条件下,由于散粒噪声中双峰结构的劈裂,在其磁交换能处出现一个振荡,其振幅随着磁交换能的增加而变小.图2与图3对应半导体的载流子均为重空穴m*/m=0.46.研究表明GaAs中还存在轻空穴载流子[35],对于轻空穴m*/m=0.12,(见图4),其散粒噪声在α=0时明显大于重空穴的数值,而α=π/4时轻空穴散粒噪声的数值却略小于重空穴的值.在图5中,当α=0时,随着磁交换能的增加,P/I的数值由小偏压下的4e值突降的位置不同,相对于h0=0下的变化位置间距为h0;当α= π/4时,P/I曲线的形状与重空穴的相同,但在峰值与振幅上轻空穴的数值均小于重空穴的数值.向和不同的磁交换能,会使得散粒噪声及噪声功率

图2 散粒噪声在磁性超导体取不同的磁交换能h0下随着偏压u的变化曲线 m*/m=0.46,z0=5.0,实线表示h0/Δ0=0,虚线表示h0/Δ0=0.2,点线表示h0/Δ0=0.4.

图3 噪声功率与平均电流的比值在磁性超导体取不同的磁交换能h0下随偏压u的变化曲线 m*/m=0.46,z0=5.0;实线表示h0/Δ0=0,虚线表示h0/Δ0=0.2,点线表示h0/Δ0=0.3,虚点线表示h0/Δ0=0.4.(a)α=0

图4 取轻空穴有效质量m*/m=0.12时的散粒噪声 z0= 5.0;实线表示h0/Δ0=0,虚线表示h0/Δ0=0.2,点线表示h0/ Δ0=0.4.(a)α=0,

图5 取轻空穴有效质量m*/m=0.12时的噪声功率与平均电流的比值 z0=5.0;实线表示h0/Δ0=0,虚线表示h0/Δ0= 0.2,点线表示h0/Δ0=0.3,虚点线表示h0/Δ0=0.4.(a)α=0,
4.结论
本文数值计算了隧道极限下半导体/磁性d波超导隧道结系统的散粒噪声和噪声功率与平均电流的比值,讨论了磁性d波超导体中磁交换能对散粒噪声的影响.研究表明,半导体中空穴载流子取不同的有效质量,及磁性超导体中取不同的晶轴取与平均电流的比值的曲线呈现不同的效应.本文所展现的散粒噪声的性质对于人们认识磁性d波超导体的特性有一定的启示,希望本文的理论结果能被实验所证实.
[1]de Jong M J M,Beenakker C W J 1996Mesoscopic Electron Transport(Berlin:Springer Press)p225
[2]Blanter YM,BügttikerM 2000Phys.Rep.336 1
[3]Camino F E,Kuznetsov V V,Mendez E E,Schäpers T, Guzenko V A,Hardtdegen H 2005Phys.Rev.B 71 020506(R)
[4]de JongM J M,Beenakker CW J 1994Phys.Rev.B 49 16070
[5]Anantram M P,Datta S 1996Phys.Rev.B 53 16390
[6]Zhu J X,Ting C S 1999Phys.Rev.B 59 R14165
[7]Tanaka Y,Asai T,Yoshida N,Inoue J,Kashiwaya S 2000 Phys.Rev.B 61 R11902
[8]AndreevA F 1964Zh.Eksp.Teor.Fiz.46 1823
[9]BüttikerM 1992Phys.Rev.B 46 12485
[10]Radovan H,Fortune N A,Murphy T P,Hannahs S T,Palm E C,Tozer SW,HallD 2003Nature425 51
[11]Won H,Maki K,Haas S,OeschlerN,Weickert F,Gegenwart P 2004Phys.Rev.B 69 180504(R)
[12]Kumagai K,Saitoh M,Oyaizu T,Furukawa Y,Takashima S, Nohara M,Takagi H,Matsuda Y 2006Phys.Rev.Lett.97 227002
[13]Saxena S S,Agarwal P,Grosche F M,Haselwimmer R K W, SteinerM J,Pugh E,Walker I R,Julian S R,Monthoux P, Lonzarich G G,HuxleyA,Shelkin I,Braithwaite D,Flouquet J 2000Nature406 587
[14]Pfleiderer C,UhlarzM,Hayden SM,Vollmer R,Lohneysen H V,BernhoeftN R,Lonzarich G G 2001Nature412 58
[15]AokiD,Huxley A,Ressouche E,Braithwaite D,Flouquet J, Brison J,Lhotel E,Paulsen C 2001Nature413 613
[16]Rourke PM C,TanatarM A,Turel C S,Berdeklis J,Petrovic C,Wei J Y T 2005Phys.Rev.Lett.94 107005
[17]Kasahara Y,Nakajima Y,Izawa K,Matsuda Y,Behnia K, Shishido H,Settai R,Onuki Y 2005Phys.Rev.B 72 214515
[18]WangQ,Hu C R,Ting C S 2006Phys.Rev.B 74 214501
[19]KarchevN I,Blagoev K B,Bedell K S,Littlewood P B 2001 Phys.Rev.Lett.86 846
[20]Singh D J,Mazin I I2002Phys.Rev.Lett.88 187004
[21]CuocoM,Gentile P,Noce C 2003Phys.Rev.Lett.91 197003
[22]Santi G,Dugdale S B,Jarlborg T 2001Phys.Rev.Lett.87 247004
[23]WalkerM B,Samokhin KV 2002Phys.Rev.Lett.88 207001
[24]Shen R,Zheng ZM,Liu S,Xing D Y 2003Phys.Rev.B 67 24514
[25]Jehl X,SanquerM,Calemczuk R,MaillyD 2000Nature405 50
[26]Yoshida N,Tanaka Y,Inoue J I,Kashiwaya S 2001PhysicaC 352 199
[27]L IXW 2006Commun.Theor.Phys.45 369
[28]Dong Z C,XingD Y,Dong J M 2001Acta Phys.Sin.50 556 (in Chinese)[董正超、邢定钰、董锦明2001物理学报50 556]
[29]Zhang P,Li Y X 2009J.Phys.:Condens.Matter.21 095602
[30]Dong Z C,Chen G B,Xing D Y,Dong J M 2000Acta Phys. Sin.49 2276(in Chinese)[董正超、陈贵宾、邢定钰、董锦明2000物理学报49 2276]
[31]Yang K,Sondhi S L 1998Phys.Rev.B 57 8566
[32]Liao Y H,Dong Z C,Yin Z F,Fu H 2008Chin.Phys.B 17 1893
[33]de Gennes P G 1966Superconductivity ofM etals and Aollys(New York:Benjamin Press)
[34]Blonder G E,Tinkham M,Klapwidjk TM 1982Phys.Rev.B 25 4515
[35]Broido D A,Sham L J 1985Phys.Rev.B 31 888
PACC:7475,7450
Shot noise in the sem iconductor/ferromagnetic d-wave superconductor tunnel junct ion
Liang Zhi-Peng1)2)Dong Zheng-Chao2)†
1)(School of Physical Science and Technology,Suzhou University,Suzhou 215006,China)
2)(Department of Physics,Huaiyin No rmal University,Huai′an 223001,China)
23 March 2009;revised manuscript
17 June 2009)
Considering the dependence of the gap on the exchange energy in ferromagnetic d-wave superconductor,we use an extended Blonder-Tinkham-Klapwijk approach to investigate the shot noise in semiconductor/ferromagnetic d-wave superconductor junction by solving the Bogoliubov-de Gennes(BdG)equation.It is shown that the exchange energyh0in the ferromagnetic d-wave superconductor may induce a split of the shot noise double-peak at zero-bias and the energy gap peak,and the interval between the two split peaks is equal to 2h0;furthermore,with the increasing exchange energyh0, the shot noise and the ratio of shot noise power to average current are restrained.
ferromagnetic d-wave superconductor,semiconductor,shot noise
†通讯联系人.E-mail:zcdong2006@hotmail.com
†Corresponding author.E-mail:zcdong2006@hotmail.com

