磁致伸缩材料磁弹性内耗的场依赖特性及其用于磁场传感研究*
卞雷祥 文玉梅 李 平
(重庆大学光电工程学院,光电技术及系统教育部重点实验室,重庆 400044)
磁致伸缩材料磁弹性内耗的场依赖特性
及其用于磁场传感研究*
卞雷祥 文玉梅†李 平
(重庆大学光电工程学院,光电技术及系统教育部重点实验室,重庆 400044)
(2009年3月23日收到;2009年6月22日收到修改稿)
分析和测试了磁致伸缩材料磁弹性内耗的偏置磁场依赖特性,发现Terfenol-D的品质因数(与内耗的量值成反比)强依赖于偏置磁场.利用磁致伸缩材料磁弹性内耗强依赖于偏置磁场的特性,提出了一种静态和准静态磁场的磁传感器方法,即将磁致伸缩材料与压电变压器单元层叠构建一种复合变压器.分析表明:在谐振状态下,复合变压器的输出电压正比于其品质因数,于是复合变压器的输出电压强依赖于偏置磁场;磁致伸缩材料的ΔE效应对复合变压器输出电压的影响很小.制备Terfenol-D/PZT8复合变压器进行了实验,结果表明,在近谐振状态下,当激励输入电压振幅为0.5 V时,复合变压器工作的输出电压对静态磁场的灵敏度达到~5.12 mV·Oe-1.
磁传感,磁弹性内耗,压电变压器,磁致伸缩材料
PACC:0755,7580,7590
1.引言
近年来磁致伸缩效应在磁传感领域得到了广泛的应用,利用磁致伸缩效应进行磁传感的原理如下:1)ΔE效应.利用磁致伸缩材料所具有的超ΔE效应,将磁致伸缩材料与压电材料复合构成复合谐振器,则复合谐振器的谐振频率是外部磁场的函数,一种非晶态铁磁合金FeCoB与压电L iNbO3复合谐振器对磁场变化的灵敏度为60 Hz·Oe-1(1Oe =79.5775 A/m)[1].2)利用磁致伸缩特性.将多层磁致伸缩材料与压电材料叠层复合,并将压电层并联连接以降低磁电响应的低频截止频率,Dong等[2]采用Terfenol-D/压电单晶Pb(Mg1/3Nb2/3)O3-PbTiO3多层叠层复合在0.01和1 Hz处可探测的最小磁场达到10-7和10-9T,或将磁致伸缩材料与谐振器件复合,利用磁致伸缩应力引起谐振器谐振频率变化以传感磁场,一种将Terfenol-D与SAW器件复合的磁传感器灵敏度为132 Hz·Oe-1[3].3)利用磁致伸缩材料压磁系数对偏置磁场的依赖特性.磁致伸缩/压电复合材料在小幅度交变磁场激励下产生的磁电电压输出依赖于外部静态磁场,一种Terfenol-D/Pb(Zr,Ti)O3叠层复合单元在0.1 Oe交变磁场激励下,谐振时输出磁电电压对静态磁场的灵敏度为~1.2 mV·Oe-1,可探测的最小磁场达10-8T或者更小[4].采用电场激励磁致伸缩/压电复合材料中压电层,利用逆磁致伸缩效应使磁致伸缩层发生振荡磁化,此时,环绕在复合材料上的接收线圈将产生感应电压,由于压磁系数依赖于外部磁场,感应线圈的感应电压依赖于外部磁场.利用该原理实现的磁传感器可探测的最小磁场在1 Hz处达8.7 pTHz-0.5[5].但该类方法需要一个线圈环绕于器件外围用于激励或者接收.
超磁致伸缩材料Terfenol-D的磁弹性内耗强依赖于偏置磁场,并且这种磁弹性内耗——偏置磁场依赖特性广泛存在于纯铁、非晶态合金(FeSiB, CoSiB)、FeNi基合金等铁磁材料中[6—9].我们提出将磁弹性内耗强依赖于磁场的特性用于静态或者准静态磁场传感,为此,将磁致伸缩材料和压电变压器叠层复合构成磁致伸缩/压电复合变压器(或者称之为磁致伸缩/压电复合双端口体波谐振器).在谐振时,复合变压器的输出特性受磁弹性内耗的影响,因此,复合变压器的输出电压将依赖于外部静态或者准静态磁场.与之前报道的磁致伸缩/压电叠层复合磁电材料用于磁传感的原理[4,5]相比,不同之处在于:1)磁致伸缩/压电复合变压器用于磁传感利用磁致伸缩材料磁弹性内耗对偏置磁场的依赖特性,而磁致伸缩/压电叠层复合磁电材料利用的是磁致伸缩材料压磁系数对偏置磁场的依赖特性;2)复合结构的压电层被设计为一个压电变压器单元,用于磁传感器时无需任何线圈用于激励或者接收.
本文分析和测试了磁致伸缩材料Terfenol-D磁弹性内耗随偏置磁场的变化特性,介绍了磁致伸缩/压电复合变压器用于磁传感的工作原理,分析了复合变压器的输出电压与系统品质因数(与内耗成反比)及有效机电耦合系数的关系.制备了Terfenol-D/PZT8复合变压器并进行实验,理论和实验定性符合,复合变压器的输出电压强依赖于偏置磁场.
2.磁弹性内耗
磁弹性内耗是铁磁材料中磁性与力学性质的耦合所引起的,磁致伸缩效应产生了磁性与力学性质的耦合[10].磁弹性内耗一般分为三类:宏观涡流、微观涡流和静滞后型.微观涡流损耗和宏观涡流损耗与频率有关,理论上这两种涡流损耗与振动的幅度无关.当频率很低时,涡流损耗则非常小,此时静滞后型内耗成为主要内耗,这是由于畴壁不可逆位移或者磁畴不可逆转动导致磁滞现象和应力-应变滞后回线.研究表明:1)磁致伸缩材料Terfenol-D应力-应变滞后环的面积及形状随偏置磁场变化而变化[9];2)Terfenol-D材料在偏置磁场叠加一缓慢变化磁场的磁化作用下,磁化曲线将围绕偏置点出现“小滞后环”,并且“小滞后环”的形状和面积与所加偏置磁场的大小有关[11,12].这意味着磁致伸缩材料中磁弹性内耗依赖于偏置磁场.
内耗的量值可用Q-1表示,其中,Q为材料的品质因数[10].可通过测试品质因数随偏置磁场的关系来反映内耗与偏置磁场的关系.在进行测试时,选用磁致伸缩材料Terfenol-D(甘肃天星稀土功能材料有限公司生产)尺寸为14 mm×2 mm×1 mm,样品纵向沿〈110〉晶轴取向.测试Terfenol-D品质因数随偏置磁场变化特性的实验系统如图1所示.一对环形Nd-Fe-B永磁体(内直径3 cm,外直径7 cm,厚度1.4 cm)用于产生偏置磁场,调节磁铁间距可改变偏置磁场大小,磁场大小使用高斯计测量;交变磁场采用长直螺线管产生.偏置磁场和交变磁场都沿样品长度方向施加.测试方法和步骤如下: 1)在不同偏置磁场下,使用交变磁场激励磁致伸缩材料产生纵向、基频振动;2)使用德国生产的Polytec OFV-5000型多普勒测振仪,测得样品端面处的振动速度˙u的振幅并改变激励磁场的频率进一步测得振动速度谱;3)采用3 dB带宽方法,计算得到其品质因数,即Qmag=fr/Δf,其中fr为谐振频率, Δf为3 dB带宽.图2所示为测得的Terfenol-D样品品质因数(Qmag)及一阶纵向振动基频随偏置磁场变化的关系曲线.由此可以看出,Terfenol-D的品质因数Qmag强依赖于偏置磁场,并且在较低水平偏置磁场的区间内品质因数随外部偏置磁场增加而单调递减.假设是一与偏置磁场有关的函数,定随偏置磁场变化的变化率为


图1 磁致伸缩材料振动特性测试系统
3.器件原理
磁致伸缩材料在外应力作用下将产生应变,这时晶体内的能量除了由于自发形变而引起的磁弹
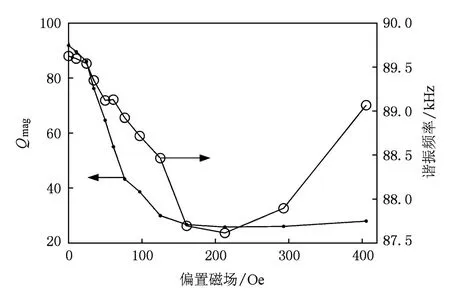
图2 Terfenol-D品质因数Qmag及谐振频率随偏置磁场变化特性
性能外,还存在着由外应力作用而产生的非自发形变的磁弹性能[13].由于磁弹性能的存在,交变应力的作用将导致铁磁体产生振荡磁化,并且振荡磁化的特性受外部偏置磁场或偏置应力的影响.对于磁致伸缩/压电叠层复合材料,压电层在外加电压激励下将产生振荡,由于压电层和磁致伸缩层之间弹性耦合的作用,磁致伸缩层和压电叠层一起产生振荡,并产生振荡磁化.由于磁致伸缩层的磁弹性内耗是外加磁场的函数,磁致伸缩/压电叠层复合振子的损耗也将随磁场变化而变化,那么磁致伸缩/压电叠层复合材料在外加电压激励下的振荡特性与外部磁场有关.磁致伸缩/压电叠层复合材料的有效品质因数Qm可由下式给出[14],

其中,Qmag和Qpiezo分别为磁致伸缩层和压电层的品质因数,nm为磁致伸缩材料所占复合材料的体积比,np=1-nm为压电材料所占复合材料的体积比.由图2可以看出,磁致伸缩材料的磁弹性内耗依赖于偏置磁场,根据(2)式,磁致伸缩/压电叠层复合材料的有效品质因数Qm必依赖于偏置磁场.
在磁传感器中,要将磁信号转换为电信号.为此,磁致伸缩/压电复合材料中压电层被设计为变压器结构.这种改进后的复合器件可称为磁致伸缩/压电复合变压器或者磁致伸缩/压电复合双端口体波谐振器.当复合变压器工作时,输入端在交变电信号作用下驱动其发生振动,由于压电效应,振动在输出端被再次转换为电信号.此过程包含电—机械—电的转换过程,其电—机和机—电的转换过程都与复合变压器单元的损耗特性有关.另外,电—机械—电的转换还分别与变压器输入端及输出端的极化方向和机电耦合系数有关.
图3所示为一种磁致伸缩/压电复合变压器及坐标定义,其中压电层一共包含三个电极,输入电极、输出电极和公共电极,它们构成变压器的输入端和输出端.图中箭头表示压电变压器的输入端和输出端沿厚度方向极化(P)及磁致伸缩层沿长度方向磁化(M).该复合变压器可通过如图4所示的等效电路模型来进行分析[15],其中Rm,Cm和Lm分别表征复合变压器的内耗、有效机械劲度系数和质量.C01和C02分别为输入端和输出端的一维截止电容,φp1和φp2分别为输入端和输出端的弹电耦合系数.由于结构对称,并且压电变压器单元输出端和输出端极化方向相同,可认为C01=C02,φp1=φp2.
为得到高的输出灵敏度,通常使用具有高输入阻抗的探测电路或者仪器来测量复合变压器的输出电压,因此在分析时假设输出端开路.利用阻抗变换方法,图4所示的复合变压器等效电路可简化为图5(a)所示的电路,再根据欧姆定律可得

根据(3)式,进一步可得

当复合变压器输入端短路时,其等效电路可以化为典型的压电振子等效电路,结果如图5(b)所示,其中,该等效电路的串联共振频率ωs(也叫机械共振频率)和并联共振频率ωp分别为[16]

在并联谐振频率ωp处,压电变压器输出幅度Vout达到最大值,此时变压比为

由(7)式可知,压电变压器的输出反比于表征复合变压器内耗的等效参量Rm.
根据电学中对品质因数的定义[17],即品质因数等于电路中所存储的能量(在动态电容C1或者动态电感L1中)与电路耗散的能量(由动态电阻R1产生)之比.则图5(b)所示的等效电路的品质因数为

其中,I为流过R1,L1和C1的电流.
由(5)和(6)式,得到该复合压电变压器输出端的有效机电耦合因子为[16]

联立(8)和(9)式得Rm的表达式后代入(7)式可得

由附录A可得,当输入端短路时,复合压电变压器输出端的有效机电耦合因子为

根据图2和(2)式复合变压器的品质因数Qm是偏置磁场的函数,根据(10)式,可得在并联谐振频率处压电变压器输出电压对偏置磁场Hdc的灵敏度为
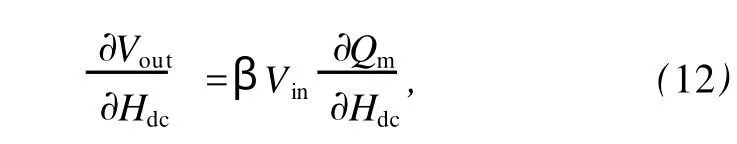
其中,
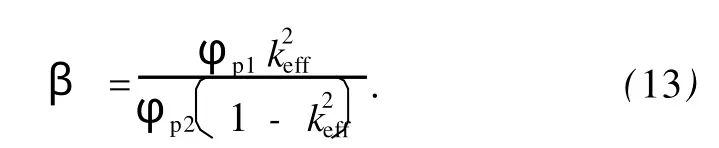
需要说明的是,对(10)式进行微分时,忽略了ΔE效应的影响,这是由于:1)磁弹性内耗对偏置磁场的依赖特性远强于ΔE效应;2)(11)式中分子分母都含有磁致伸缩材料的弹性柔顺性参数,一定程度上削弱了ΔE效应的影响.因此,偏置磁场变化对β的影响很小.
由(12)式,磁致伸缩/压电复合变压器用于磁传感的输出灵敏度可通过改变输入电压的幅度来控制,并且β越大,输出电压对偏置磁场变化的灵敏度越高.进一步分析(13)式可知:β反应了压电变压器输入端和输入端机电耦合特性及材料体积比对磁传感灵敏度的影响,变压器输入端的弹电耦合因子越大,输出端的机电耦合系数越大,β越大,灵敏度也就越高.因此,采用具有高机电耦合系数的压电材料和极化形式(如Rosen型压电变压器,输入电极厚度极化,输出电极纵向极化[15]),能够进一步提高β值及其灵敏度.

图3 磁致伸缩/压电复合变压器配置和坐标定义 (a)磁致伸缩/压电复合变压器配置,(b)坐标定义

图4 复合压电变压器的等效电路模型
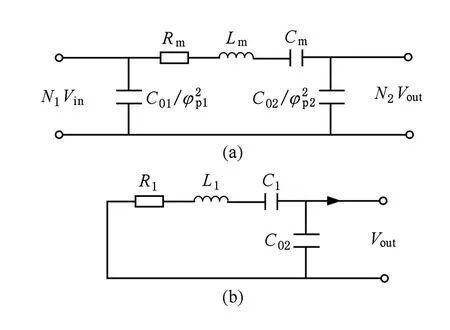
图5 变换后的等效电路模型 (a)复合变压器变换后的等效电路模型,(b)输入端短路时变换模型
4.计算及讨论

表1 复合变压器品质因数、有效机电耦合系数平方以及变压比随偏置变化特性
由图6和表1可知:1)Terfenol-D/PZT8复合变压器品质因数Qm随压电层所占复合变压器体积比np的增加而增加,但ΔQm则随压电层所占体积比np增加而减小;2)复合变压器的ΔQm低于Terfenol-D的ΔQmag,根据(2)式可知这是由于压电层的品质因数与偏置磁场无关,复合变压器的与Terfenol-D材料的相比被降低了nm倍,nm为磁致伸缩材料所占复合结构的体积比.由图7和表1可知:1)随偏置磁场变化,这源于ΔE效应,但由于(11)式中分子分母都含有磁致伸缩材料的柔顺性系数参数,随偏置磁场的变化很小,即Δ随压电材料所占体积比增大而增大则随压电相所占体积比增加而减小;3)相对于Δ在数值上相当小,因此,ΔE效应对压电变压器谐振输出幅值影响很小,在(12)式中忽略ΔE效应是合理的.由图8和表1可知:1)由于偏置磁场变化很小,Vout/Vin随偏置磁场的变化规律主要由Qm决定,Vout/Vin和Qm随偏置磁场的变化规律基本一致; 2)复合变压器的变压比随压电层所占体积比增大而增大,但则随压电层所占体积比增大而减小,这与Qm的变化规律一致;3)相同体积比时,稍小于ΔQm,这是由于随偏置磁场变化的趋势与Qm随偏置磁场变化的趋势相反,如图7(b)所示.
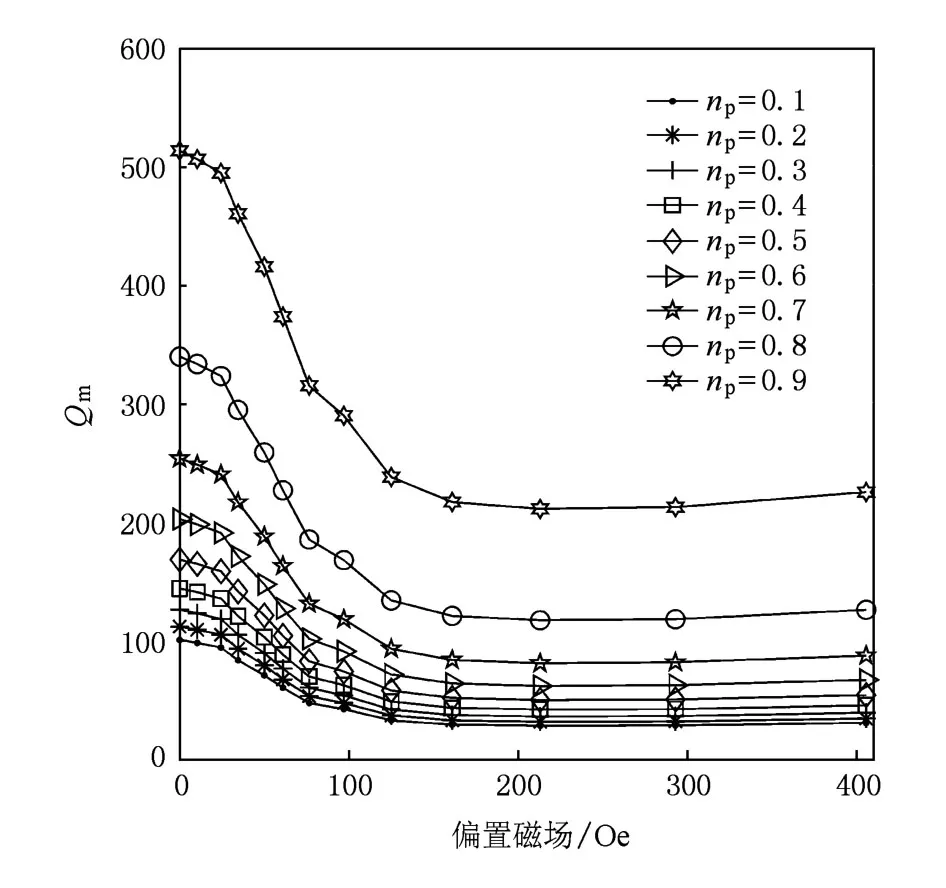
图6 不同体积比下复合变压器品质因数随偏置磁场的变化曲线
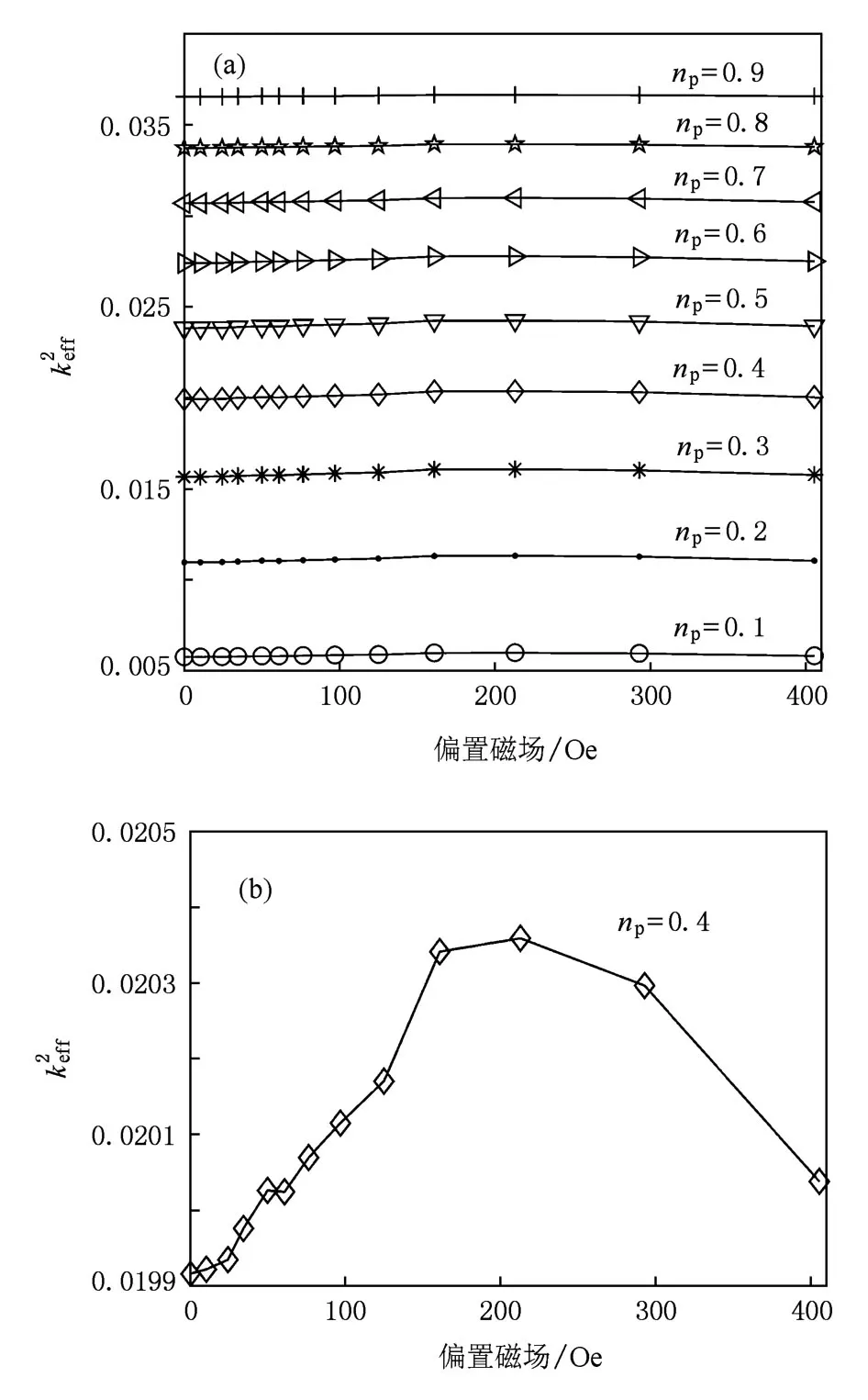
图7 不同体积比下复合变压器有效机电耦合系数平方随偏置磁场变化曲线 (a)np=0.1—0.9,(b)np=0.4时放大图
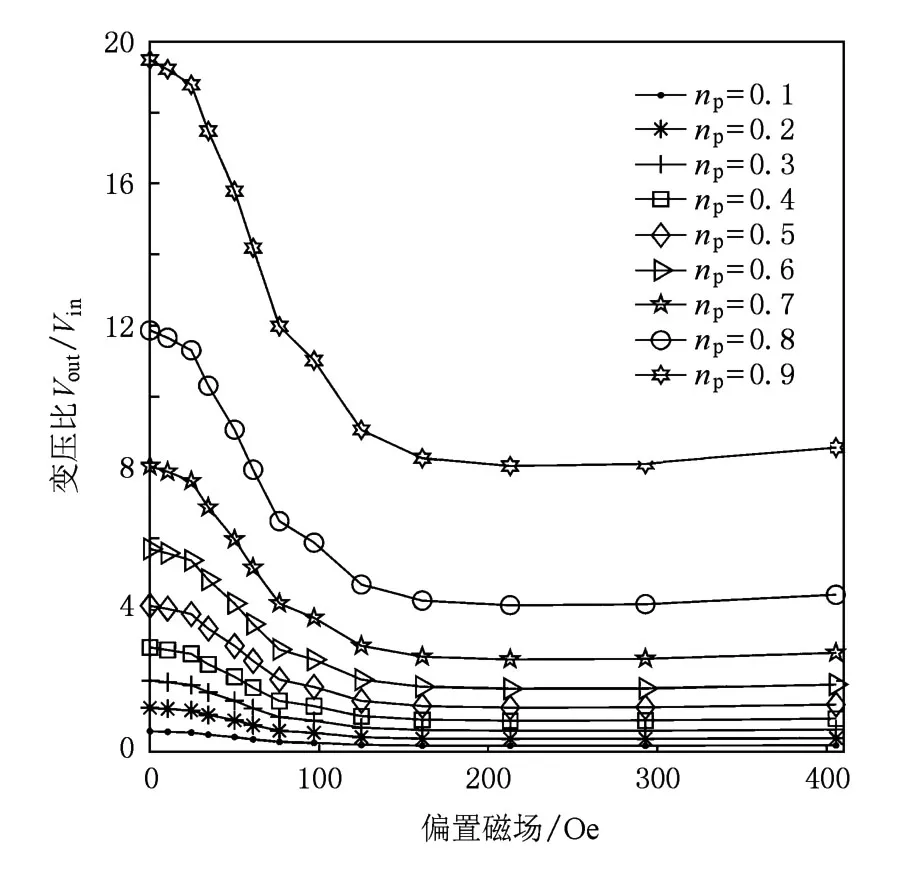
图8 不同体积比下复合变压器变压比随偏置磁场变化曲线
5.实验及讨论
实验时磁致伸缩材料仍选用Terfenol-D,样品尺寸为14 mm×2 mm×1 mm,长度方向沿〈110〉晶轴取向.压电变压器材料选用PZT8,其电极配置和极化方向如图3所示.压电变压器样品的尺寸为15 mm×2 mm×0.8 mm,其中上表面两电极(输入电极和输出电极)的间隙约为0.3 mm.在制备复合材料时,将磁致伸缩Terfenol-D和压电材料PZT8用有机溶剂清洗干净后,再用环氧树脂胶粘剂按照如图3配置将两种样片对称粘结(粘合后压电PZT8两端分别比Terfenol-D长出0.5 mm,长出部分用于焊接电极引线).
测试复合变压器输出特性时采用如图9所示的实验系统.信号发生器输出一个正弦信号激励复合变压器.复合变压器输出信号首先接入一高输入阻抗放大滤波器(Stanford SR560,输入阻抗:100 MΩ//25 pF),消除工频干扰后接入示波器测量得到输出电压.调节激励源的频率则可以测得输出电压随频率变化的曲线(即输出电压幅度谱).

图9 复合变压器特性测试系统

根据附录A中C02的公式,可得C02=166 pF,而实验所用高输入阻抗放大滤波器的输入电容Cin为25 pF,加上测试线缆杂散电容Cc的影响,实验值要小于理论值.
从图11可知,磁致伸缩材料磁弹性内耗对偏置
图10为测得的复合变压器在不同偏置磁场下输出电压幅度-频率变化曲线.测试时,输入端激励电压幅度为0.5 V.显然,复合变压器输出电压幅度谱的峰值和外部偏置磁场有关.进一步得到复合变压器谐振点处的输出电压(峰值)-偏置磁场变化的曲线如图11所示.根据(10)式计算得复合变压器在幅值为0.5 V输入激励下谐振点处的输出电压-偏置磁场变化曲线如图12所示.比较图11和图12可知:理论计算得到的输出电压幅值大约为实验值的2.1—2.4倍(随偏置磁场不同而有所不同),但理论计算的结果与实验结果的变化趋势一致,理论和实验定性符合.理论和实验在输出幅度上的差异来源于如下两个方面:1)理论计算时并未考虑胶层的影响,实际上,胶层的存在导致磁致伸缩层和压电层之间非理想耦合,将引入一定的损耗,因此,复合变压器的有效品质因数和有效机电耦合因子的实际值小于理论值;2)在理论分析时,并没有考虑复合变压器输出端所连测试线缆的杂散电容和测试仪器的输入阻抗,如果考虑进去,则复合变压器的等效电路变为如图13所示,其中,Cc为测试线缆的杂散电容,Cin为测试仪器的输入电容.此时C02→C02+Cc+Cin,实验时复合变压器所连滤波放大器输入电阻Rin已足够大(100 MΩ),故(10)式可变为磁场的依赖特性可用于探测静态或者准静态磁场.在实际应用中,可采用一个恒定频率和幅度的电压信号激励复合变压器使其工作在近谐振状态.图14为复合变压器在幅度为0.5 V、频率为97910 Hz输入电压激励下,输出电压-偏置磁场变化曲线.比较图11和图14可知,两种工作模式下的输出电压大小随偏置磁场变化的特性稍有差异,这主要是由于ΔE效应引起压电变压器的谐振频率漂移引起,但是两种工作模式下输出电压的变化趋势基本一致.复合变压器输出电压-偏置磁场变化呈现出非线性特性,在实际应用时一般要施加偏置磁场使其工作在线性区.由图14可知,在40—100 Oe区间范围内,复合变压器的输出电压都具有较好的线性特性,此时输出电压对静态磁场的灵敏度达到~5.12 mV·Oe-1.通过使用具有高变压比的压电变压器和磁致伸缩材料复合,输出灵敏度还可以进一步提高.

图10 不同偏置下复合变压器输出电压-频率曲线

图11 复合变压器谐振点处输出电压-偏置磁场曲线
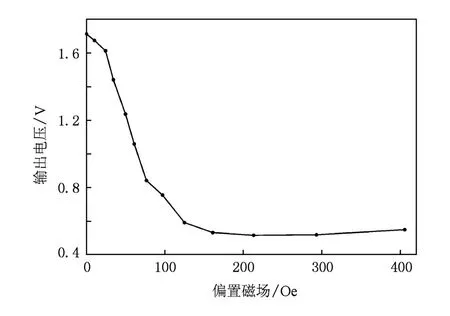
图12 复合变压器谐振点处输出电压-偏置磁场曲线(理论值)

图13 考虑输出端所接线缆电容和测试仪器输入电容后,复合变压器等效电路

图14 固定频率97910 Hz激励下复合变压器输出电压随偏置磁场变化曲线
6.结 论
分析和测试了磁致伸缩Terfenol-D磁弹性内耗与偏置场的关系,发现超磁致伸缩材料Terfenol-D的品质因数强依赖于磁场,利用该特性设计了一种可用于探测静态或者准静态磁场的磁致伸缩/压电复合变压器.由于磁致伸缩/压电复合变压器的变压比正比与其品质因数,并且品质因数强依赖于静态磁场,复合变压器的输出电压依赖于偏置磁场.采用Terfenol-D和压电材料PZT8制作了Terfenol-D/PZT8复合变压器进行了实验,实验结果和理论分析结果定性符合.通过施加一稳态偏置磁场使其工作在线性区,在幅度为0.5 V输入电压激励下复合变压器输出电压对静态磁场的灵敏度达到~5.12 mV·Oe-1.
附录A
复合变压器结构对称,建立如图A1所示的坐标系.考虑到复合变压器输入端和输出端在连接处(图A1中坐标原点位置)位移和作用力连续,再根据等效电路法[18],可以得到磁电伸缩/压电叠层复合变压器的等效电路如图A2所示,其中npρp+ρmnm,k=ω/v;是磁致材料沿着长度方向的柔顺性系数,分别是压电材料的柔顺系数、压电常数以及介电常数,ρp和ρm分别是压电材料和磁致伸缩材料的密度,A=Am+Ap为叠层材料横截面积,Am=tmw和Ap=tpw分别为磁致伸缩层和压电层的横截面积,tm和tp分别为磁致伸缩层和压电层的厚度,w为叠层材料的宽度.˙u1和˙u2分别是两端面处的振动速度,F1和F2分别为两端面处的作用力.
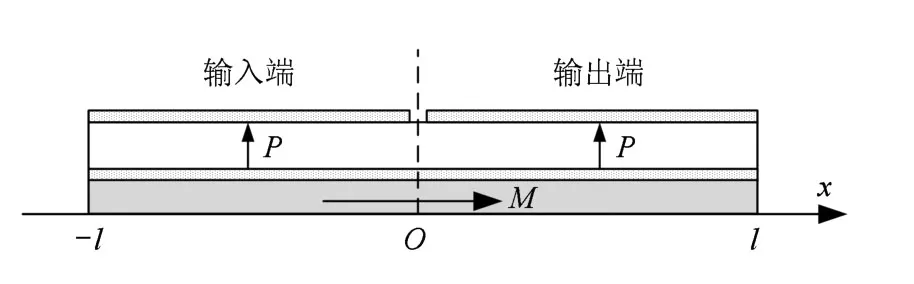
图A1 复合压电变压器坐标示意图

图A2 复合变压器机电等效电路
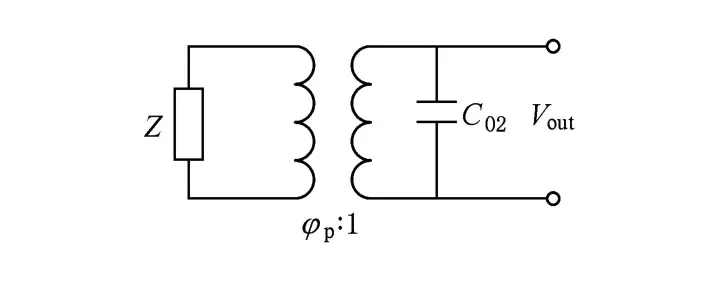
图A3 自由边界条件下输入端短路时的等效电路
在自由边界条件下(F1=F2),并且压电变压器输入端短路时,图A2等效电路可进一步简化为图A3所示的等效电路,其中阻抗Z的表达式为

根据图A3,输出端导纳为

当Y→∞时,对应的频率近似为机械谐振频率(串联谐振频率)fs,此时要求tanksl→∞,由此可得

当Y=0时对应的频率近似为并联谐振频率fp,此时有

联立(A3)和(A4)式可得


其中Δf=fp-fs.

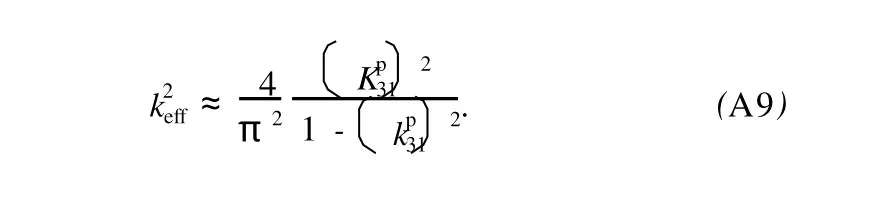
则(A6)式可化为

[1]Yoshizawa N,YamamotoI,Shimada Y 2005IEEE Trans. M agn.41 4359
[2]Dong S X,Zhai J,Xing Z,Li J F,Viehland D 2005Appl. Phys.Lett.86 102901
[3]ZhengM,Wen Y M,Li P 2007Chin.J.Sens.Actuators20 1947(in Chinese)[郑 敏、文玉梅、李 平2007传感技术学报20 1747]
[4]Dong S X,Zhai J,Li J F,Viehland D 2006Appl.Phys.Lett. 88 082907
[5]MermelsteinM D,Dandridge A 1987Appl.Phys.lett.51 545
[6]Zhen W G,Zhang J X 1987Acta Phys.Sin.36 37(in Chinese)[曾文光、张进修1987物理学报36 37]
[7]Squire P T,Atkinson D 1995IEEE Trans.M agn.31 1239
[8]Wuttig M,Su Q,Masson F,Quandt E,Ludwig A 1998J. Appl.Phys.83 7264
[9]Wun-FogleM,Restorff J B,Clark A E,Snodgrass J 2003IEEE Trans.M agn.39 3408
[10]Tian S 2004M aterials Physical Capability(Beijing:Beijing Univ.Aeronautics and Astronautics Press)p412(in Chinese) [田 莳2004材料物理性能(北京:北京航空航天大学出版社)第412页]
[11]Calkins F T,Smith R C,Flatau A B 2000IEEE Trans.M agn. 36 429
[12]JilesD C 1992IEEE Trans.M agn.28 2602
[13]Wang B W,Cao S X,Huang W M 2008M agnetostrictive M aterial and Device(Beijing:Metallurgical Industry Press) pp15,16(in Chinese)[王博文、曹淑瑛、黄文美2008磁致伸缩材料与器件(北京:冶金工业出版社)第15,16页]
[14]Yang F,Wen YM,Li P,ZhengM,Bian L X 2007Acta Phys. Sin.56 3539(in Chinese)[杨 帆、文玉梅、李 平、郑敏、卞雷祥2007物理学报56 3539]
[15]Zhang F X 2002M odern Piezoelectricity(Beijing:Science Press) (in Chinese)[张福学2002现代压电学(下册)(北京:科学出版社)]
[16]IEEE Standard on Piezoelectricity 1987IEEE Std.176
[17]Feng G P 2008Resonant Sensing Theory and Devices(Beijing: Tsinghua Univ.Press)(in Chinese)[冯冠平2008谐振传感理论及器件(北京:清华大学出版社)]
[18]Dong S X,Zhai J Y 2008Chin.Sci.Bull.53 2113
PACC:0755,7580,7590
The field dependence ofmagnetoelastic damping in magnetostrictive material and its application in the magnetic field sensing*
Bian Lei-Xiang Wen Yu-Mei†Li Ping
(Key Laboratory forOptoelectronic Technology&Systems of M inistry of Education,College of Optoelectronic Engineering,
Chongqing University,Chongqing 400044,China)
23 March 2009;revised manuscript
22 June 2009)
The magnetoelastic damping in magnetostrictive material is investigated.It is noted that the quality factor(the inverse measure of damping)of giant magnetostrictive material Terfenol-D is strongly dependent on bias direct current (DC)magnetic field.Taking advantage of the DC field dependence of magnetoelastic damping in magnetostrictive material,a DC or quasistatic magnetic sensor is proposed.The sensor is designed as a composite piezoelectric transformer (CPT)which is fabricated by bonding magnetostrictive material and piezoelectric transformer in layers.Theoretical analysis shows that the output voltage of the CPT is directly proportional to the quality factor of the CPT.Therefore,the output voltage of the CPT also strongly depends on DC field due to the strong field dependence effect of quality factor in magnetostrictive material.In addition,theΔEeffect of magnetostrictive material has little influence on the magnitude of the output voltage.A Terfenol-D/PZT8 composite transformer is fabricated for experiment.The experimental results show that the output sensitivity to DC field achieves~5.12 mV·Oe-1when the CPT is driven near resonance by an AC voltage with amplitude of 0.5 V.
magnetic sensing,magnetoelastic damping,piezoelectric transformer,magnetostrictive material
*国家高技术研究发展计划(批准号:2007AA12Z132)、国家自然科学基金重点项目(批准号:50830202)和国家自然科学基金委员会与中国工程物理研究院NSAF联合基金(批准号:10776039)资助的课题.
†通讯联系人.E-mail:ymwen@cqu.edu.cn
*Project supported by theNationalHigh TechnologyResearch andDevelopment Program ofChina(GrantNo.2007AA12Z132),the Key Program of the NationalNatural Science Foundation of China(GrantNo.50830202),and the Joint Fund of the NationalNatural Science Foundation of China and the China Academy of Engineering Physics(GrantNo.10776039).
†Corresponding author.E-mail:ymwen@cqu.edu.cn

