中国土地投资函数的参数估计

柴志春，赵 松，吴凌燕，李众敏

（1.中国土地勘测规划院，北京100035；2.北京工业大学实验学院，北京101101；3.中国社会科学院世界经济与政治研究所，北京100732）

中国土地投资函数的参数估计

柴志春1，赵 松1，吴凌燕2，李众敏3

（1.中国土地勘测规划院，北京100035；2.北京工业大学实验学院，北京101101；3.中国社会科学院世界经济与政治研究所，北京100732）

研究目的：推导中国的土地投资函数，解析土地价格对投资的影响因子，并以北京、上海、宁波、广州、天津、沈阳6城市为样本进行地区影响分析。研究方法：计量经济法，模型分析法。研究结果：土地价格每上升1个百分点，工业投资就会下降0.00765个百分点。上海、宁波、广州、天津4个城市的医药、电子和食品制造业投资对土地价格变化最为敏感。研究结论：土地价格对工业投资有一定影响，工业投资对土地价格的弹性有明显的行业和地区特点。

土地经济；土地投资函数；工业用地

研究土地价格与工业投资的数量关系，对制定和完善中国现有的土地调控政策有着极为重要的现实意义和理论价值，同时也是运用土地价格参与宏观调控、刺激工业经济增长等宏观政策的基础。

现有研究主要体现以下两个方面：一是构建工业用地生产函数；二是构建宏观经济的投资函数。关于工业用地的生产函数分析，李明月等[1]通过构造柯布—道格拉斯生产函数，研究三要素（土地、劳动力、资本）对整个经济的影响。宏观经济的投资函数分析上，王军等[2-3]从宏观经济学的角度研究利率、国民收入等对投资的影响。综上所述，目前国内研究中侧重于土地与投资之间函数关系的研究较少，尤其是对不同行业的投资关系尚未涉及。

本文拟通过理论分析构造中国土地投资函数，确定工业用地价格与工业投资之间数量关系，并以北京、上海、宁波、广州、天津、沈阳6城市为样本，采集1998—2008年间的土地价格和投资等数据，进行分行业（化学工业、医药、金属产品制造业、建材、电子、纺织业、机械设备制造业、轻工、电力、食品制造业10个行业）的实证研究[4]。

1 中国土地投资函数的理论框架

土地成本是经营成本中的一项，而经营成本直接影响利润，因此，本文从利润决定的投资方程式（加速模型）入手研究。式1为利润决定的投资方程式，根据这一方程，当期的合意资本存量是由当期的利润决定的，而当期的投资取决于资本存量增加以及上一期资本的折旧[5-6]。

式1简化得到投资方程式2：

式2进一步简化为：

也就是说，当期的投资是当期利润以及上一期资本存量的函数，式3是土地投资函数估计中的第一个方程式。式1—3中，K为资本存量；V为利润；I为投资；δ为折旧率；λ为加速因子；其他符号为方程参数。

接下来，对利润V进行分解，将土地成本（或土地租金）引入到模型之中，根据会计恒等式，企业利润是增加值减去成本和税收（式4）。

式4中，Y、C、T分别代表增加值、成本、税收。而成本又由劳动力成本、融资成本和土地成本3个部分构成：

式5中，labor、capital和land分别表示劳动力、融资、土地。假设企业的劳动力成本、融资成本、土地成本分别取决于当期的工资水平、利率和租金水平（分别表示为w，ir和re）。在回归中，将式5简化为式6。式6是设定的成本决定方程：

这是在估计土地投资函数时，需要估计的第二个方程①需要说明的是，这是获得弹性系数的一种方法，还可以采用经验的方法，即根据土地成本在工业成本中的比例来确定b3值。假设土地成本占工业成本的比例为u，而土地租金与土地成本之间的弹性值为1，那么当土地租金变化1%时，工业成本将变化u%，所以u就是所需要的弹性值，b3=u。实际上，在后面的计算中，由于回归式结果不理想，最终采取了经验值的方法。。

把式4和式6代入式3后，可以得到I与re之间的关系：

式7所表达的只是投资与土地租金水平之间的函数关系，还没有直接涉及土地价格，需要进一步分析土地租金与土地价格之间的关系。因此，对土地价格与土地租金按以下方程式进行回归[7]：

式8中，P表示土地价格。这是在后面的参数估计中，需要估计的第三个方程，用以确定土地价格与土地成本（租金）之间的关系。将式8的结果代入式7，可以得到：

根据式9，得到投资与土地价格之间的弹性e：

在得到式10中的弹性e之后，基本上就确定了土地价格与当期投资之间的关系。但是要注意的是，这只是一个平均值，为得到不同地区、不同行业的弹性值，需要进行分地区、分行业的调整[8-9]。

从理论上看，影响不同行业、不同地区的弹性的主要因素是不同行业的资本—土地比率（K/L），或者说是单位土地上的资本密集度，以及不同地区的人口密度。但是由于这方面的数据非常缺乏，所以进行调整是非常困难的。但是，仍有可能根据调研的数据来完成这方面的调整。调整思路如下：

假设有m个地区和n个产业，通过式1—9的理论框架，最终得到的是如式12所示的弹性矩阵。

通过式1—12，得到不同地区、不同产业中土地价格对投资的影响。由于理论方法和数据都比较缺乏，在进行地区和产业调整时，使用了相对简单的调整方法。

2 中国土地投资函数的参数估计

根据上述理论框架，对相关参数进行估计，并最终得出如式12所示的弹性矩阵。由于最新数据尚没有发布，有些数据来自于调查，在回归式中，采用的数据仅截至2007年。

2.1 投资函数参数估计

根据式3，投资函数采用了利润决定的加速模型，具体形式为：It=d0+d1Vt+d2Kt-1。在回归过程中，I为全社会固定资产投资额；V为规模以上企业利润；K为规模以上企业资产总规模。由于企业利润、资产总额数据难以获得，而且历史数据口径与现有数据不一致，在回归中仅使用了1998—2007年的数据。式13为回归结果。

式13中，R2=0.984，调整后的R2=0.979，即d1=1.761125。

回归结果表明，中国的投资行为有典型的利润驱动现象，利润每上升1个百分点，投资额将会上升1.76个百分点以上。

2.2 成本函数参数估计

根据前文介绍，可以采取两种方法获得企业成本对土地租金的弹性值。在分析过程中，首先采用了第一种方法，回归结果表明，这一方法所得的结果并不理想，主要是因为无法获得对应年份土地租金的绝对数值。因此，采取第二种方法，即根据经验值估计的方法。

依据数据可得情况，以深圳市为例对土地成本的占比进行估计。深圳市共有工业用地264.91 km2，2005年深圳市工业企业主营业务成本为81086933万元。根据相关研究[10]，2000年深圳的土地租金水平为154.78万元/hm2，另根据全国土地租金指数变化，假设深圳的工业用地租金的变化与全国的情况是一致的①因为缺乏全国范围的实际租金水平统计数据，在本研究中，只能以深圳的数据作为参照进行测算。，到2005年，深圳的土地租金水平应为158.27万元/hm2。当年，土地租金总额为4192730.6万元（158.27万元/hm2×26491 hm2），占工业企业主营业务成本的比例为5.2%。

根据这一经验值，设定企业成本与土地租金的弹性系数为0.052，即：b3=0.052。

2.3 土地租金函数参数估计

以上只得出了成本与土地租金之间的关系，为了分析土地价格与工业投资的关系，需要确定土地价格与土地租金之间的关系。根据式8，假定两者之间的理论关系为ret=α+βPt。本文中，采用工业土地价格指数以及工业用地租金指数进行回归。

R2=0.552，调整后的 R2=0.503，即 β =0.083454。

通过以上步骤，得到所有计算全国平均弹性系数所需的参数：d1=1.761125，b3=0.052，β=0.083454。将上述参数值代入式10中，可算出全国平均的弹性系数。

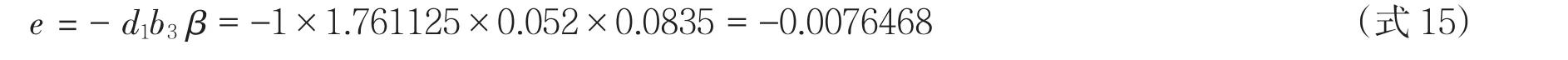
从式15可以看出，就全国平均而言，土地价格对工业投资有一定的影响，虽然这一影响是非常有限的②需要注意的是，式15代表的只是一般情况。当土地价格超过一定的区间时，两者的函数关系会有较大的变化，这里对后一种情况不再细述。，土地价格每上升1个百分点，工业投资就会下降0.00765个百分点。反之，工业投资将上升0.00765个百分点。当然，这只是一个平均的弹性系数，为了得到不同地区、不同产业的弹性系数，还需要进行产业和地区的调整。

2.4 系数调整与最终结果

第一部分中，详细阐述了系数调整的具体办法，主要是通过确定地区调整因子和产业调整因子，得到式11所示的i地区j产业的弹性系数，并最终得到各地区所有产业的弹性系数矩阵。

（1）地区调整系数。地区调整因子是由不同地区人口密度决定的，以全国的人口密度为参照系，用各地区的人口密度除以参照值，得到地区调整系数（表1）。

（2）产业调整系数。由于没有全国的资本密集度数据，本文采用季晓峰的调查数据[11]，该成果调查了江苏省各行业的资本密集度，以各行业平均值为参照系，然后用不同行业的资本密集度除以平均值，得到产业调整系数（表 2）。

表1 地区调整系数Tab.1 Regional adjustment coefficients

（3）弹性系数矩阵。通过表1和表2得到调整系数矩阵，包括不同地区、不同产业的综合调整系数（表3），并根据调整系数矩阵得到不同地区、不同行业的弹性系数矩阵（表4）。

在得到全国平均的工业投资—土地价格弹性系数之后，再根据不同地区的人口密度、不同行业的资本密集度，进一步调整可得不同地区、不同行业的投资—土地价格弹性系数矩阵。

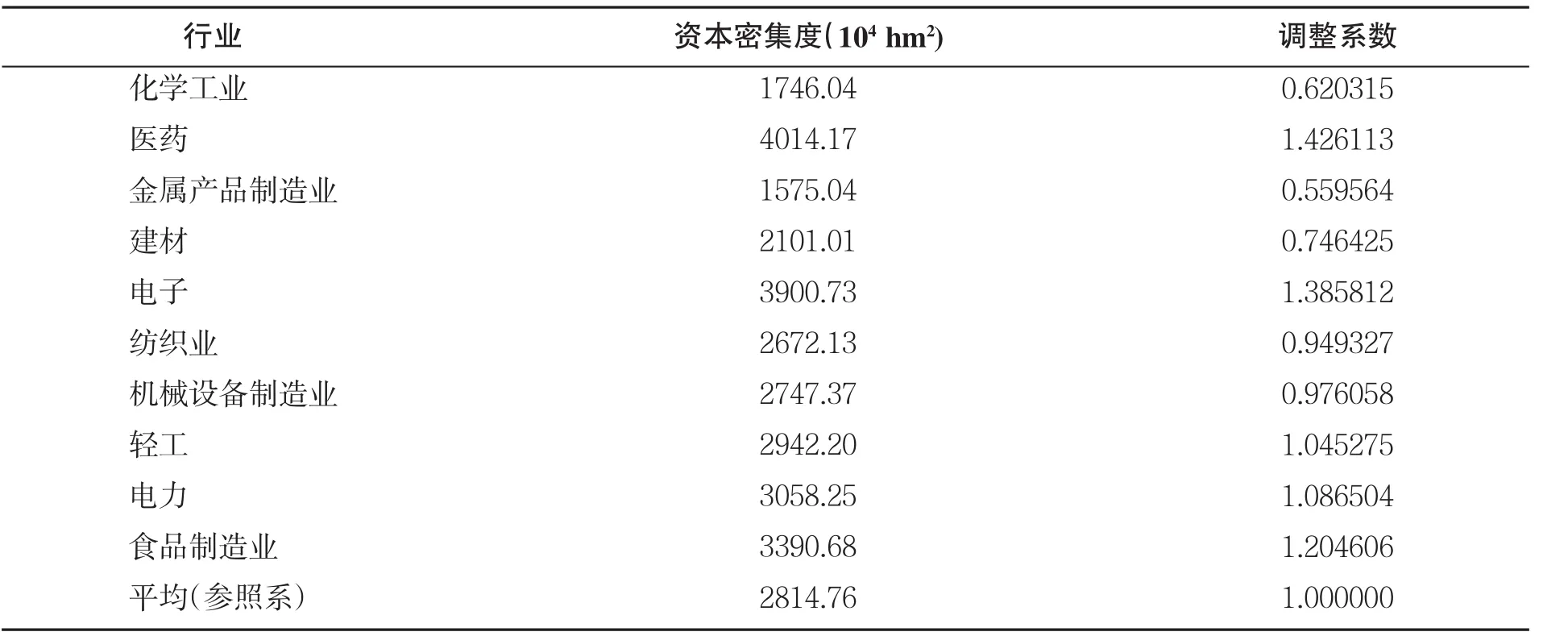
表2 产业调整系数Tab.2 Industry adjustment coefficients

表3 各地区不同产业的调整系数矩阵Tab.3 Adjustment coefficient matrix of different industries in various regions

3 结论

根据本文分析，可以较明确地看出，土地价格的确对土地投资起到了一定的作用，工业投资与土地价格之间的弹性系数为-0.00765，即土地价格每上升1个百分点，工业投资就会因此下降0.00765个百分点，反之亦然。

同时，也可以看出土地价格影响工业投资的程度不是很大。这主要是由两个方面的原因导致的：第一，土地成本在企业成本中所占的比例较小，只有5.2%，导致弹性系数中的b3值很小，只有0.052。这也是由工业部门的特点决定的，如果是像房地产业这样的产业，土地成本对企业成本的占比高，土地价格的变化引起的投资变化要比工业部门大得多。第二，土地价格对土地租金的影响较小，因为土地价格并不是直接的投资成本，与土地价格相关的土地租金水平才是影响投资的直接变量，由于中国土地价格对土地租金的影响很小，导致了弹性系数计算公式中的β值非常小，只有0.083454，也就是说，土地价格涨了一倍，土地租金才上涨8.3%的水平。

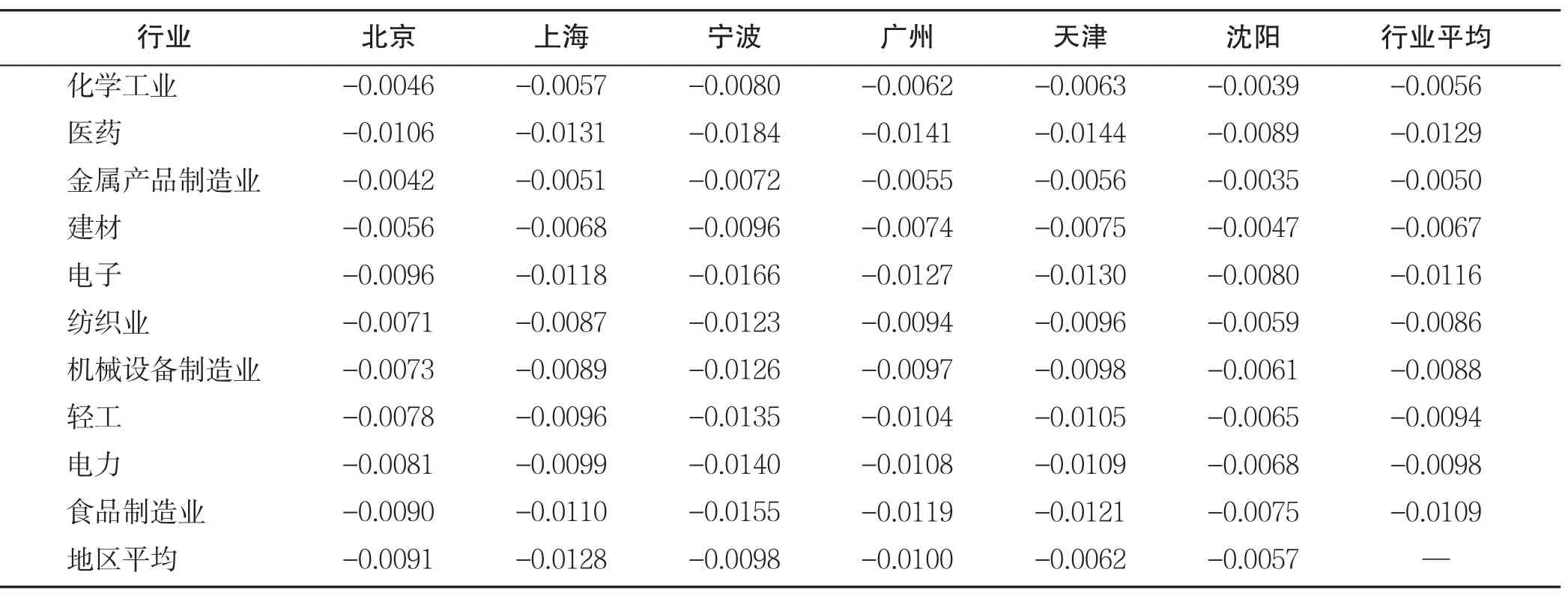
表4 各地区不同产业的弹性系数矩阵Tab.4 Elastic coefficient matrix of different industries in various regions

此外，工业投资对土地价格的弹性有明显的行业和地区特点，一些资本密集度高的产业（医药、电子、食品制造业等行业），由于在单位土地上的投资规模较大，当土地价格变化时，引起投资的变化较大，达到1%以上。同时，在东部地区（上海、宁波、广州）和北京，由于人口密度较大，也导致工业投资对土地价格更为敏感，尤其是上海，工业投资对土地价格变动的弹性系数超过1%。受行业和地区因素影响，上海、宁波、广州、天津4个城市的医药、电子和食品制造业的投资对土地价格变化最为敏感。

（References）：

［1］李明月，胡竹枝.土地要素对经济增长贡献的实证分析——以上海市为例［J］.软科学，2005，（6）：21-23.

［2］王军.中国投资函数的实证分析［J］.当代经济科学，2001，（3）：19-24.

［3］国家统计局固定资产投资统计司.中国投资问题量化研究［M］.北京：中国统计出版社，1997.

［4］谢名一，王季.中国工业用地价格调整与外国直接投资关系研究［J］.科技创业月刊，2007，（6）：9-10.

［5］刘红忠.投资学［M］.北京：高等教育出版社，2008.

［6］樊潇彦，袁志刚.宏观经济学［M］.北京：高等教育出版社，2008.

［7］甘藏春.土地宏观调控创新理论与实践［M］.北京：中国财政经济出版社，2009.

［8］上海社会科学院房地产业研究中心，上海市房产经济学会.土地供给在宏观调控中的传导［C］.上海：上海社会科学院，2007.

［9］杨志荣.土地供给政策参与宏观调控的理论与实证研究——基于风险控制的视角［M］.西安：电子科技大学出版社，2009.

［10］张靖，张军连，张风荣.留地安置所引发的思考？［J］.河南国土资源，2003，10：19-21.

［11］季晓峰.江苏省主要工业行业土地集约利用研究［D］.南京：南京农业大学，2006.

Parameter Estimation for Land Investment Function of China

CHAI Zhi-chun1,ZHAO Song1,WU Ling-yan2,LI Zhong-min3
（1.China Land Surveying and Planning Institute,Beijing 100035,China;2.The Pilot College of Beijing University of Technology,Beijing 101101,China;3.Institute of World Economics and Politics,Chinese Academy of Social Sciences,Beijing 100732,China）

The purposes of this paper are to deduce the land investment function of China,analyze the influential actors of land prices to the investment,and to analyze the regional influences by taking 6 cities,i.e.,Beijing,Shanghai,Ningbo,Guangzhou,Tianjin and Shenyang,as samples.Methods employed include econometrics and model analysis.The results indicate:（1）the industrial investment amount will drop 0.00765%if the land prices increase 1%;（2）the nvestment amounts in medical,electronic and food manufacturing industries in Shanghai,Ningbo,Guangzhou and Tianjin are the most sensitive to the variation of land prices.It is concluded that the land prices have certain influences on industrial investments and there exist remarkable industrial and regional features in the elasticity of industrial nvestments to land prices.

land economy;land investment function;industrial land

F301.24

A

1001-8158（2010）07-0053-06

2009-12-30

2010-01-11

柴志春（1978-），女，江西万年人，博士。主要研究方向为土地经济。E-mail:chaizhichun@sina.com