分数布朗运动下红利亚式期权定价公式

王志明,徐 娟

(武汉科技大学理学院,湖北武汉,430065)

分数布朗运动下红利亚式期权定价公式

王志明,徐 娟

(武汉科技大学理学院,湖北武汉,430065)

在假定股票价格遵循由分数布朗运动驱动的随机微分方程的条件下,利用分数布朗运动随机分析理论,得到具有固定执行价格且有红利支付的几何平均亚式期权定价公式。

分数布朗运动;几何平均亚式期权;红利

亚式期权是一种新型期权,在到期日,亚式期权的损益依赖于合同期内某段时间标的资产的平均价格。亚式期权是当今金融衍生品市场上交易最为活跃的奇异期权之一,因此研究亚式期权具有较大的现实意义。经典期权定价公式的推导是基于标准布朗运动随机分析理论。文献[1-2]在假设股票价格服从标准布朗运动的条件下,采用鞅方法推导了亚式期权的定价公式。

近年来,许多学者研究发现利用分数布朗运动驱动的随机微分方程来描述资产价格变化更加合理,并开始从事有关分数布朗运动的理论及应用研究。文献[3-4]在标的资产价格服从分数布朗运动模型的假设条件下,得到了期权定价的相关结论。考虑到股票发红利这一情况,本文在股票价格满足分数布朗运动的假设条件下,讨论带红利的几何平均亚式期权的定价,对分数布朗运动环境下亚式期权定价模型进行了推广。

1 假设条件

设{WHt,t≥0}是定义在风险中性概率测度空间(Ω,F,P)上的分数布朗运动,其中,H为Hurst参数,H∈(0,1)。考虑一无摩擦的金融市场,并且该市场仅包含两种证券:一种无风险资产(债券)与一种有风险的标的资产(如股票)。设债券价格Bt与股票价格St分别满足方程

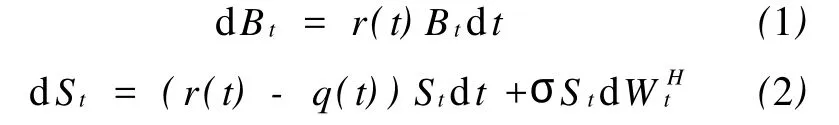
式中:r(t)为无风险利率,q(t)为红利率,均假定为时间t的函数,t∈(0,T),其中 T为到期日;σ为标的资产的瞬时波动率,设为常数。

2 公式推导

引理1[4]随机微分方程式(2)的解为

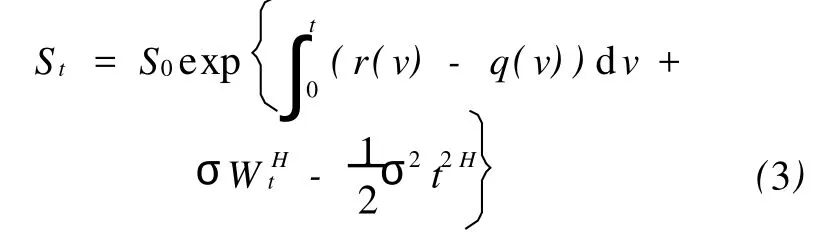
引理2[4]对于欧式未定权益ξ∈FHT,且ξ∈L2(P),则ξ的价格满足

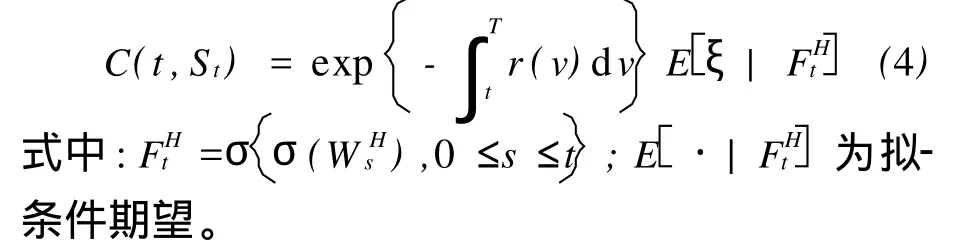
假定亚式期权执行价格为 K,到期日为 T,则几何平均亚式看涨期权损益为[5]

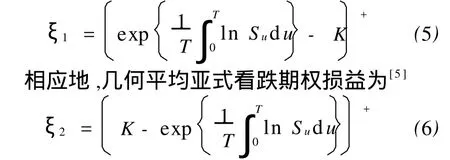
定理1 设无风险利率 r(t)与红利率q(t)均为时间t的可积函数,则几何平均亚式看涨期权价格为

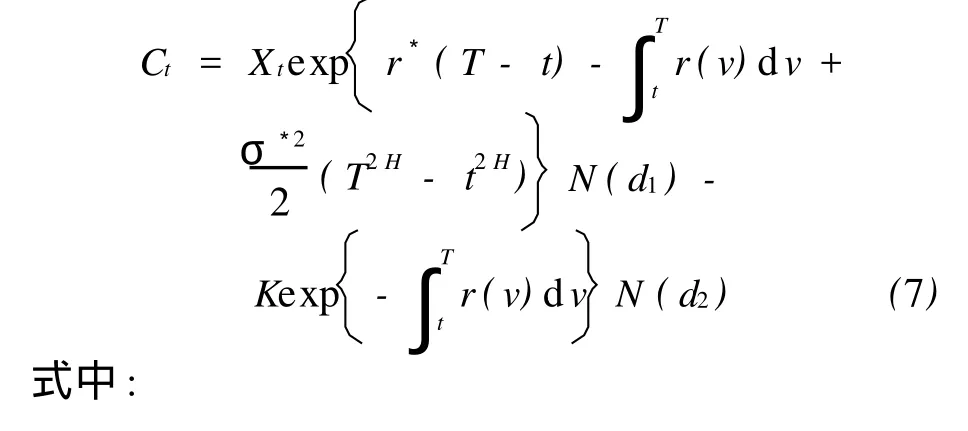
推论1 设无风险利率 r(t)与红利率 q(t)均为时间t的可积函数,则几何平均亚式看跌期权价格为

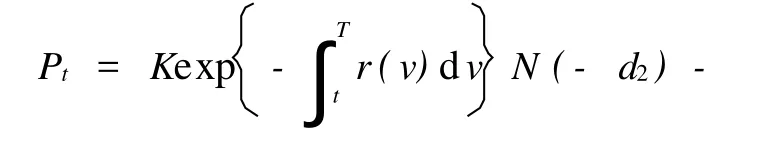
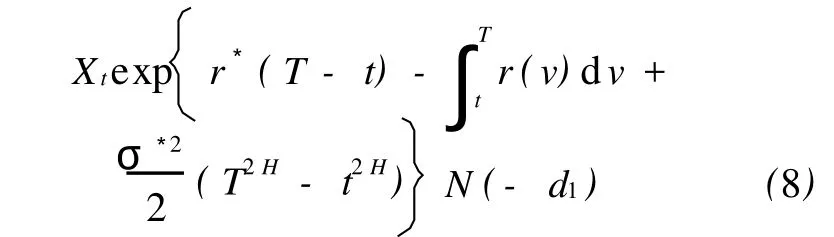
证明 在此条件下,几何平均亚式看涨、看跌期权平价关系为

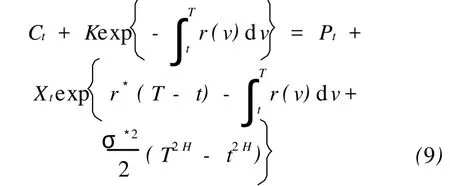
将Ct的值代入式(9),化简即得到式(8)。证毕。

若 r(t)=r,即无风险利率为常数,则ξ的价格满足[7]

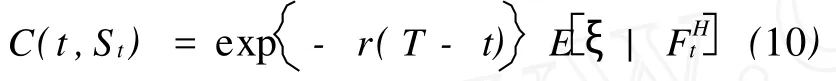
定理2 设红利率q(t)为时间t的可积函数,无风险收益率为常数,则几何平均亚式看涨期权价格为

推论2 设红利率q(t)为时间t的可积函数,无风险收益率为常数,则几何平均亚式看跌期权价格为

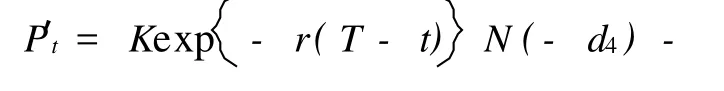
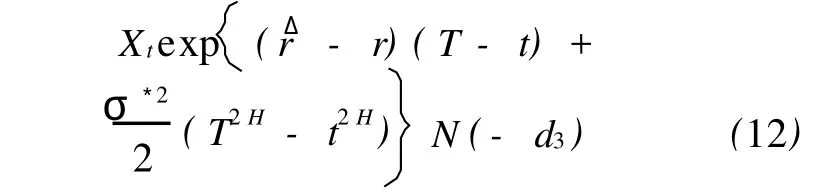
证明 在此条件下,几何平均亚式看涨、看跌期权平价关系为

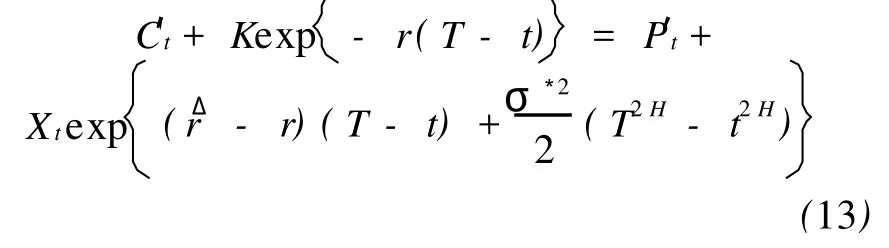
将 C′t的值代入式(13),化简即得到式(12)证毕。

3 结语

分数布朗运动下的期权定价公式比传统的Black-Scholes期权定价公式更能解释资本市场的价格变化现象,因为期权的价格除了与资产价格S、时刻 T和t有关,还与Hurst参数 H有关当 H=1/2,且不考虑红利因素时,即得到布朗运动环境下的几何平均亚式看涨、看跌期权以及平价关系[5]。本文研究结果是对文献[5]研究结果的一种推广。

[1] 郭娜,刘新平.支付红利的几何亚式期权定价模型[J].吉首大学学报,2009,30(3):28-30.

[2] 柳洪恩,孔繁亮.几何型亚式期权定价中的鞅方法[J].哈尔滨理工大学学报,2010,15(1):80-82.

[3] 阳小红.分数布朗运动下几何平均亚式期权定价[J].科技信息,2009(4):12-13.

[4] 刘韶跃.数学金融学的分数型Black-Scholes模型及应用[D].长沙:湖南师范大学,2004.

[5] 金治明.数学金融学基础[M].北京:科学出版社, 2006:186-193.

[6] Elliott R J,van der Hoek J.A general fractional w hite noise theo ry and app lications to finance[J]. Mathematical Finance,2003,13(2):301-330.

[7] Necula C.Op tion p ricing in a fractional Brow nian motion environment[R].Bucharest:Center for Advanced Research in Finance and Banking,Bucharest University of Economics,February,2002.

The dividend Asian option pricing in fractional Brown ian motion

W ang Zhim ing,Xu Juan
(College of Science,Wuhan University of Science and Technology,Wuhan 430081,China)

This paper,based on the assump tion that stock p rice satisfies fractional Brow nian motion and emp loying the theo ry of stochastic analysisof fractional Brow nian motion,obtains geometric average A sian op tion p ricing w hich is characterized by fixed imp lemented p rice and dividend payment.

fractional B row nian motion;geometric average A sian op tion;dividend

O211.6

A

1674-3644(2010)06-0665-04

[责任编辑 尚 晶]

2010-10-12

国家自然科学基金资助项目(60904060).

王志明(1962-),男,武汉科技大学副教授.E-mail:mingwz@126.com