简介水泥实验室常用样本分布特征值的Excel计算

孙庆利

（济南大学工程训练中心，山东济南250022）

简介水泥实验室常用样本分布特征值的Excel计算

孙庆利

（济南大学工程训练中心，山东济南250022）

以水泥实验室常用样本分布特征值为例，运用Excel进行数据分析的辅助计算，显示了Excel运算迅速、准确的优点。

样本分布特征值Excel函数计算

研究或统计分析的对象的全体元素组成的集合称为总体或母体。在统计工作中，可以根据产品的质量管理规程或实际工作需要，选定总体的范围，如每个月的出厂水泥，某一批进厂煤或原材料，都可视为一个总体。要了解总体的性质，理论上必须对全部个体的性质进行测定，这在实际中往往是不可能的。在实际工作中只能从总体中抽取一定数量的、有代表性的个体组成样本，通过对样本的测量，并借助数理统计手段，对总体的分布中心和标准偏差进行推断，从而掌握总体的性质。

来自总体的部分个体的集合，称为样本或子样。样本中所含样品的个数称为样本容量或样本大小。若样本容量适当大，并且抽样的代表性强，则通过检测得到的分布特征值，就能很好地代表总体的分布特征值。在实际运用中，为了对总体情况有一个概括了解，需要用几个数字表达出总体情况。这少数几个数字在数理统计中称为特征值。因此，在进行统计推断前确定样本分布的特征值，具有重要的实用价值。

常用的样本分布特征值分为两类：一是位置特征值；二是离散特征值。

位置特征值一般是指平均值，它是分析计量数据的基本指标。它们表达了数据的集中位置。反映了数据共同趋向的平均水平。位置特征值一般包括算术平均值、几何平均值、加权平均值、中位数、众数等。

离散特征值用来表示一组测量数据波动程度或离散性质，是表示一组测定值中各测定值相对于某一确定的数而言的偏差程度。一般是把各测定值相对于平均值的差异作为出发点进行分析。常用的离散特征值有平均差、极差、方差、标准偏差、变异系数等。

下面就对使用Excel工具对水泥实验室常用样本分布特征值的计算进行简要介绍。

1 表示样本分布位置的特征值（样本分布中心）

1.1 算术平均值

将一组测定值相加和，除以该组样本的容量（测定所得到的测定数据的个数），所得的商即为算术平均值。设有一组测定数据，以x1，x2，…，xn表示。这组数据共由n个数据组成，其算术平均值见式（1）：

式中：x1，x2，…，xn——各测量值；

n——样本的容量。

例1：对水泥中三氧化硫含量（%）的测定，得到10个数据：2.8、2.9、2.6、2.7、2.8、2.8、2.9、2.8、2.8、2.6。

Excel计算如下：输入各测定值；选中“B4”单元格；选择常用函数“=AVERAGE（B3:K3）”；然后点击“确定”即可得到其算术平均值为2.77，见图1。

图1 算术平均值的计算

1.2 加权平均值

加权平均值是考虑了每个测量值的相应权的算术平均值。将各测量值乘以与其相应的权，将各乘积相加后，除以权数之和，即为加权平均值。其计算公式如下。

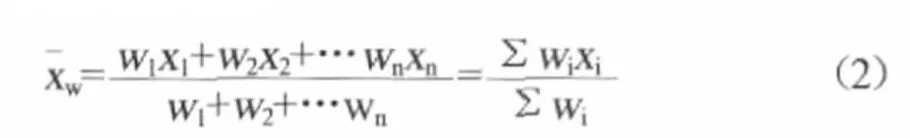
式中：x1，x2，…xn——各测量值；

w1，w2，…wn——各测量值相应的权；

Σwi——各相应权的总和；

Σwixi——各测量值与相应权乘积之和。

例2：某水泥企业有三台回转窑。1号窑年产20万吨熟料，平均抗压强度为58.5MPa；2号窑年产15万吨熟料，平均抗压强度为57.8MPa；3号窑年产12万吨熟料，平均抗压强度为59.2MPa。求全厂全年生产的熟料的综合抗压强度。

Excel计算如下：输入各测定值和权；选中“B5”单元格；输入公式“=B3*B4”点击“确定”再用鼠标左键点击“B5”单元格，B5就被黑框框住，而且在黑框的右下角有个小黑方块，将鼠标移动到这个小黑方块（填充句柄）上，鼠标变成“+”的形状，此时按下鼠标向右拖至D5，再释放鼠标，其它的分子值就计算出来了。这里将这种方法称为填充句柄法。

选中“E5”单元格，选择常用函数“SUM（B5: D5）”；然后点击“确定”即可得到整个分子之和；

选中“E4”单元格，选择常用函数“SUM（B4: D4）”；然后点击“确定”即可得到整个权之和；

选中“B6”单元格，输入公式“=E5/E4”，然后点击“确定”即可得到加权平均值。见图2。

图2 加权平均值的计算

1.3 中位数

中位数也是表示频率分布集中位置的一种特征值。其意义是将一批测量数据按大小顺序排列，居于中间位置的测量值，称为这批测量值的中位数。当测量值的个数n为奇数时，第（n+1）/2项为中位数；当测量值的个数n为偶数时，位居中央的两项之平均数即为中位数。

例3：对出磨水泥每2小时测定一次三氧化硫含量，某日共得12个测量值：2.86、2.91、2.65、2.70、2.82、2.73、2.88、2.92、2.75、2.84、2.77、2.85。求这组测量值的中位数。

Excel计算如下：输入各测定值；选中“B4”单元格；输入统计函数“=MEDIAN(B3:M 3)”,然后点击“确定”即可得到中位数。见图3。

图3 中位数的计算

1.4 众数

众数是指在一组测量数据中出现次数最多的测量值。

例4：某水泥企业控制出磨水泥的细度（筛余）范围为7.0%±1.0%。每小时测定一次，某日早班的测量数据（%）如下：7.4、7.1、7.8、7.4、7.5、7.4、7.6、7.5。

Excel计算如下：输入各测定值；选中“B4”单元格；输入统计函数“=MODE（B3:I3）”,然后点击“确定”即可得到众数为7.4，见图4。

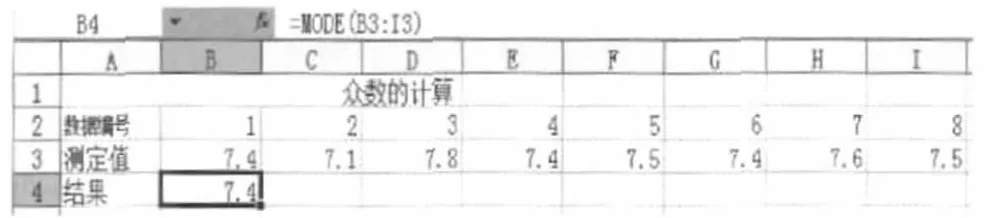
图4 众数的计算

1.5 均方根平均值

均方根平均值是各测量值平方之和除以测量值个数所得商值的平方根。计算式如下：

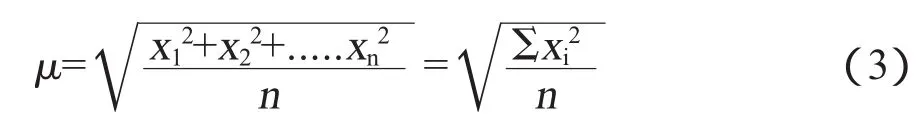
式中：x1，x2，…，xn——各测量值；

n——测量值的个数；

Σxi2——各测量值的平方之和。

例5：某班对出磨水泥细度的测量值（筛余%）为：7.2、7.3、7.4、8.8、7.9、7.6、7.4、7.5。求该班出磨水泥的平均细度。

Excel计算如下：输入各测定值；选中“B4”单元格；输入公式“=POWER（B3，2）”点击“确定”再用鼠标左键点击“B4”单元格，B4就被黑框框住，运用填充句柄法，按下鼠标向右拖至I4，再释放鼠标，其它的测量值的平方就计算出来了。

选中“J4”单元格，选择常用函数“SUM（B4: I4）”；然后点击“确定”即可得到整个测量值的平方之和。

图5 均方根平均值的计算

选中“B5”单元格，输入公式“=SQRT（J4/8）”，然后点击“确定”即可得到均方根平均值。见图5。另外一个方法：输入各测定值；选中“B4”单元格；输入函数“=SQRT（SUMSQ（B3:I3）/8）”,然后点击“确定”也可得到均方根平均值。

2 表示测量值离散性质的特征值

2.1 极差R

极差是最简单、最易了解的表示测量值离散性质的一个特征值。极差又称全距，或范围误差，即在一组测量数据中最大值与最小值之差，见下式：

例6：测得三块试体的抗压强度为58.7、57.8、59.2、59.8、58.4、58.8（MPa），求此组试体的抗压强度的极差。

Excel计算如下：输入各测定值；选中“B4”单元格；输入函数“=MAX（B3:G3）-M IN（B3:G3）”，然后点击“确定”即可得到极差为2，见图6。

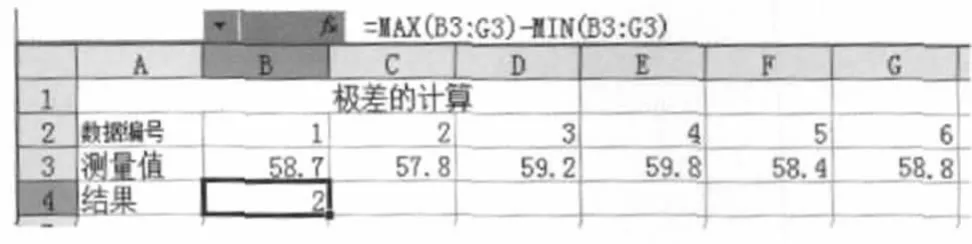
图6 极差的计算

2.2 平均绝对偏差

一组测量数据中各测量值与该组数据平均值之偏差的绝对值的平均数，称为平均绝对偏差，见下式。

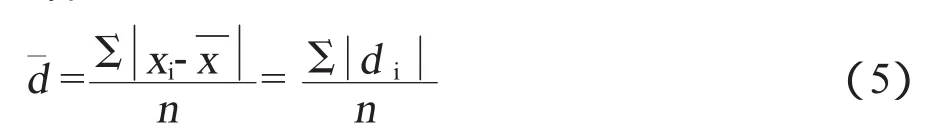
式中：d——平均绝对偏差；

di——某一测量值xi与平均值x之差。

例7：以氟硅酸钾容量法测定某水泥熟料样品中二氧化硅的含量（%），所得结果为：21.50、21.53、21.48、21.57、21.52。计算该组测量结果的平均绝对偏差。

Excel计算如下：输入各测定值；选中“B4”单元格；输入函数“=ABS[B3-AVERAGE（$B$3:$F $3）]”,然后点击“确定”即可得到x1与平均值之差。再用鼠标左键点击“B4”单元格，B4就被黑框框住，运用填充句柄法，此时按下鼠标向右拖至F4，再释放鼠标，其它的测量值与平均值之差就计算出来了。然后点击B5输入公式“=SUM（B4:F4）/5”，再点击“确定”则得到平均绝对偏差为0.024，见图7。

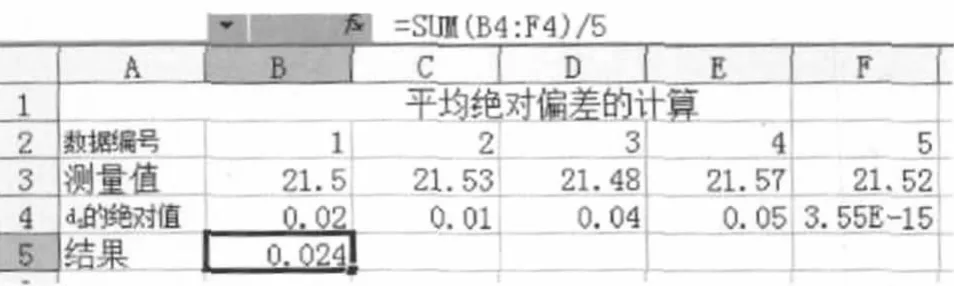
图7 平均绝对偏差的计算

另外一个方法：输入各测定值；选中“B4”单元格；输入统计函数“=AVEDEV（B3:F3）”，然后点击“确定”也可得到平均绝对偏差。

2.3 方差

方差是指各测量值与平均值的偏差平方和除以测量值个数而得的结果。采用平方可以消除正负号对差值的影响。

总体方差以δ2来表示，但在实际工作中，往往用样本的方差s2来估计总体的方差。s2的计算式如下：

式中：xi——样本中每个测量值（变量）；

x——样本平均值；

n——样本容量。

例8：某厂有一台水泥磨，在同一班里测定了出磨水泥的细度（筛余%）：7.4、7.5、7.6、8.0、7.9、7.6、7.6、7.5。计算其方差。

Excel计算如下：输入各测定值；选中“C4”单元格；输入公式“=C3-AVERAGE（$C$3:$J$3）”,然后点击“确定”即可得到x1与平均值之差。再用鼠标左键点击“C4”单元格，C4就被黑框框住，运用填充句柄法，此时按下鼠标向右拖至J4，再释放鼠标，其它的测量值与平均值之差就计算出来了（注，参考文献[1]的4号数据计算有误）。然后点击C5输入公式“=C4^2”，点击“确定”即可。然后点击C5，它就被黑框框住，运用填充句柄法，此时按下鼠标向右拖至J5，再释放鼠标，其它的测量值与平均值之差的平方值就计算出来了。然后点击C6，输入公式“=SUM（C5:J5）/（8-1）”便得到结果为0.042679，见图8。

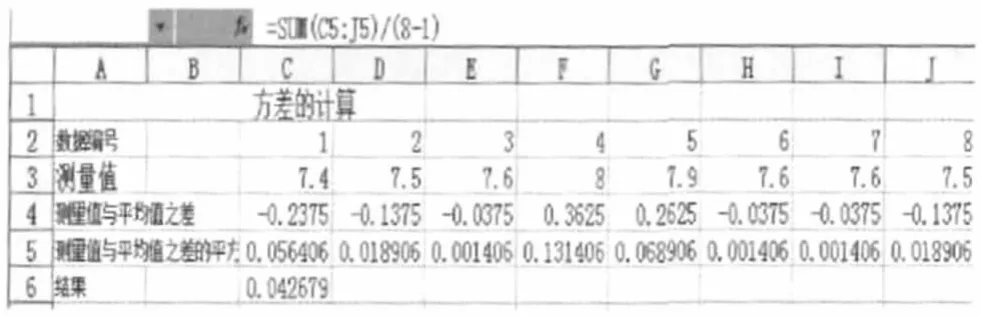
图8 方差的计算

另外一种方法：输入各测定值；选中“B4”单元格；输入统计函数“=VAR（B3:I3）”,然后点击“确定”也可得到方差。

2.4 标准偏差

标准偏差又称标准差或均方差、均方根差。在描述测量值离散程度的各特征值中，标准偏差是一项最重要的特征值，一般将平均值和标准偏差两者结合起来即能全面地表明一组测量值的分布情况。

总体标准偏差以δ来表示，但在实际工作中，以样本标准偏差s来估计总体标准偏差，这时，s的计算式如下：

式中：s——总体标准偏差估计值，简称样本标准偏差，或实验标准偏差；

x——样本平均值；

n-1——样本自由度（记为f），n为样本容量。

例9：水泥熟料中二氧化硅测定结果（%）为：21.50、21.53、21.48、21.57、21.52、21.56、21.52、21.53、21.46、21.48。计算该组数据的标准偏差。

Excel计算如下：输入各测定值；选中“B4”单元格；输入统计函数“=STDEV（B3:K3）”，然后点击“确定”即可得到标准偏差为0.035355，见图9。

图9 标准偏差的计算

关于变异系数的计算读者可以按照上面的计算分别计算出它的分子部分和分母部分，然后自行求出数据的变异系数，这里从略。

[1]中国建筑材料检验认证中心、国家水泥质量监督检验中心编著.水泥实验室工作手册[M].第一版，北京：中国建材工业出版社，2009年.

[2]苏华等编著.Excel2003函数在办公中的应用[M].第一版，北京：人民邮电出版社，2007年.

（编辑：张茕莺）

TQ172.16 文献标识码：B 文章编号：1007-6344（2010）03-0045-04

2009-10-20】