试论向量在几何中的应用
□陆金菊
(山西省畜牧兽医学校,山西 太原 030024)
试论向量在几何中的应用
□陆金菊
(山西省畜牧兽医学校,山西 太原 030024)
向量在解决数学问题中有着广泛的用途。利用向量知识解决几何问题可以将“定性”研究转变为“定量”分析,使复杂问题简单化。从而,使学生掌握“数形”结合的方法,提高解决问题的能力。
向量;几何;数量积;向量垂直;应用
向量在数学领域中有着广泛的应用。在几何中引入向量可以使几何问题代数化,从而降低平面几何与立体几何的思维难度,将原来繁难地“找、作”过程转变为定量计算,进而体现算法数学的魅力。笔者将从下面三个方面研究向量在几何中的应用。
我们知道三角形的三条高相交于一点,有很多方法可以证明这个结论。但用向量垂直的充分必要条件来证明该结论,则证明过程更显得简捷明了。下面给出具体的证明过程。
求证:△ABC三边上的高相交于一点。
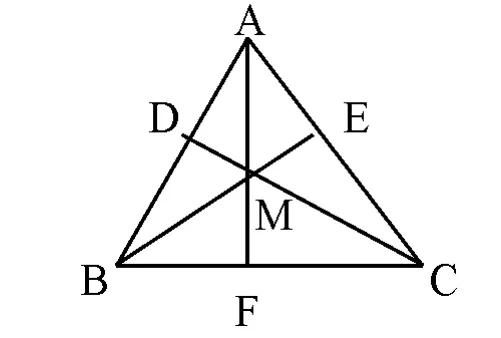
证明:如下图在△ABC中,设M是AB和AC边上的高CD和BE的交点,连结AM并延长,交BC边于F。只要能证明AF是BC边上的高即可。
一、向量在平面几何中的应用
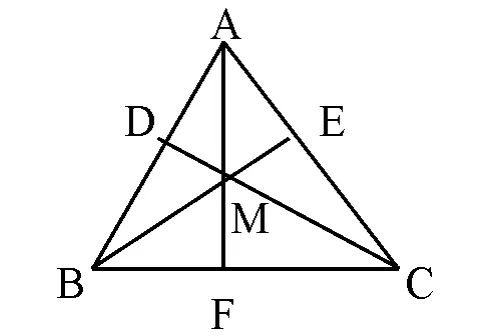

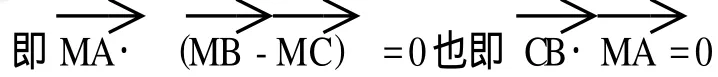
∴MA⊥CB 而M是AF上的一点
∴FA⊥CB 即AF是BC边上的高
这就证明了△ABC三边上的高相交于一点M。
由此可见,在平面几何中要证明线线垂直时,应用向量垂直的充要条件是一种很好的方法。这种证法不仅简单明了,而且学生还容易接受,从而大大降低了教学难度,给我们证明垂直问题提供了一条捷径。同理,在平面几何中要证明多线共线的问题时,我们可以应用向量平行的充要条件去解决。
二、向量在立体几何中的应用
在立体几何有关点、线、面位置关系的判定中以及各类角度的计算问题中,应用向量知识往往能使空间结构转化为代数结构。进而把空间的“定性”研究转化为代数的“定量”分析。从而,使求解目标程序化、算法化,有利于学生克服空间想象力弱的障碍,降低立体几何的难度。
例 (如下图)在四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=,DC=SD=2点M在侧棱SC上,∠ABM=60°
(Ⅰ)证明M是侧棱SC的中点;
(Ⅱ)求二面角S—AM—B的大小。
证明:∵SD⊥平面ABCD
∴以D为坐标原点、射线DA为x轴的正半轴建立如上图所示的坐标系D—XYZ。

三、向量在解析几何中的应用
例 以抛物线y2=2px(p>0)上任意点M(x0,y0)为顶点,是否存在抛物线的内接正三角形?
分析:为了寻找以M(x0,y0)为顶点的抛物线的内接正三角形是否存在,可以先假设这样的正△MQN存在。这样,由于△MQN为正三角形,所以利用向量M点旋可求得Q、N两点的坐标。而M、 Q、N三点都在抛物线上,故建立以t、α为参数的参数方程。如果能证明参数t、α存在实数解,则可知满足条件的正三角形存在。
由于方程(4)是sinα,cosα的三次齐次方程,而sinα≠0,cosα≠0。所以,方程(4)可化为同解的tanα的三次方程,并存在一实根tanα1,且sinα1≠0,cosα1≠0。从(2)得y0
2+2ty0sinα+t2sin2α=2px0+2ptcosα即t sin2α=2p cosα-2y0sinα

该例说明向量在解析几何中也大有用武之地。一般地,用向量知识解决一些解析几何或立体几何问题时,往往可以根据题意建立适当的坐标系,这样不但给数形结合之间的转换和公式的应用创造了必要条件,而且还可以避免添加辅助线等麻烦。
由此可见,向量在解决数学问题的过程中有着广泛的用途。因此我们在平时的数学教学中,应重视向量知识的学以致用。引导和鼓励学生善于运用它,从而提高他们解决问题的能力。
[1]陈振宣.向量教学的探索[J].数学教学,2003,(3).
[2]任高峰.利用空间向量探索“点”位置[J].数学教学,2003, (10).
On Application of Vector in Geometry
Lu Jinju
(ShanxiAni mal Husbandry and Veteri nary School,Taiyuan,Shanxi,030024)
Vector has a universal use in the process of solving maths problems.Solving geometry problem by using vector knowledge can change qualitative research into quantification analysis,simplify the complex problems,make studentsmaster the method of combination of"figures"and"shapes",i mprove the students ability to solve the prob2 lems.
vector;geometry;dot product;vector vertical;application
G633.63
B
1008—8350(2010)01—0049—02
本文责编 安春娥
2009—10—10
陆金菊(1965—),女,山西介休人,山西省畜牧兽医学校,讲师。

