在役平台结构疲劳评估的工程计算法

冯国庆, 任慧龙, 陈北燕, 李 辉

(哈尔滨工程大学,哈尔滨 150001)

在役平台结构疲劳评估的工程计算法

冯国庆, 任慧龙, 陈北燕, 李 辉

(哈尔滨工程大学,哈尔滨 150001)

论述了疲劳谱分析方法的基本原理,研究了在役平台的结构疲劳强度评估的工程计算方法,并以该方法对某一在役半潜式平台进行了疲劳强度的评估。结果表明,该方法易于实施,所作评估比较合理。

在役平台;结构;疲劳强度

Abstract:The basic theory of spectral fatigue analysis is discussed.The engineering caculation of structural fatigue strength assessment for aging platform structures is investigated.As an example,the fatigue assessment of an aging platform is proposed.The results show that this method is easy to be acomplished and the assessment is reasonable.

Key words:aging platform;structure;fatigue strength

0 前言

对于不断遭受交变载荷作用的海洋平台而言,结构的疲劳破坏是其主要的失效模式之一。特别是已经服役多年的在役平台,由于腐蚀,磨损等因素的影响,使得平台结构抵抗疲劳破坏的能力不断下降,为此对在役平台结构疲劳作出评估,从而确定剩余疲劳强度和剩余疲劳寿命,对在役平台结构安全和延寿具有理论意义和工程应用价值。本文对在役平台的疲劳强度评估方法进行了研究并给出了可行的工程处理方法。

1 疲劳谱分析方法的基本理论

海洋波浪的长期状态通常可以看成是由许多短期海况的序列组成。对每一短期海况,把波浪作为一个平稳正态随机过程来研究。某一海况在给定浪向角θ时的交变应力过程可视为均值为零的窄带平稳随机过程,其应力范围 S服从Rayleigh分布,概率密度函数为

式中:S表示应力范围;σX为交变应力过程的标准差。

上述给定浪向角θ时的应力交变过程的功率谱密度(方差密度)表示为 GX(ωe,θ),其值可利用(2)式得到

式中:H(ωe,θ)为应力响应频响函数;ωe为船舶的遭遇频率;θ为浪向角;Gη(ωe,θ)为用遭遇频率表示的波能谱,一般取为两参数的PM谱。

将 m0,m2分别表示为功率谱密度的0次矩和2次矩,则有

交变应力过程的标准差σX可按(4)式得到,即

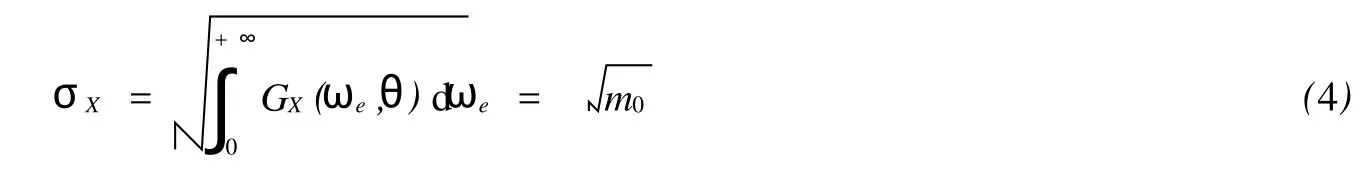
交变应力过程的跨零率 f0的表达式为

式中:f0ij为该应力交变过程的跨零率,由式(5)给出;Tij·f0ij为该航行状态期间内应力范围循环次数;fSij(S)为该期间的短期应力范围分布。

设所考虑的回复期为 Td,平台工作区域有nS个海况,各海况出现的概率为pi,划分的浪向数为nH个,各浪向出现的概率为 pj,则式(6)中的 Tij=Td·pi·pj。再将 fSij(S)的表达式(1)代入式(6),经积分整理后,可得回复期内的疲劳累积损伤度 DT为

设所考虑的平台在第 i海况和第j浪向中工作时间为 Tij,并用 Dij表示在 Tij期间的累积损伤度,根据Miner线性累计损伤理论,Tij期间的疲劳累积损伤度可表示为

2 在役平台疲劳评估工程计算法

对于已服役过一段时间的结构构件,考虑其服役期间的疲劳损伤 DP及该损伤的不确定因素α,可得到节点的剩余疲劳强度DR:

式中 FD F为疲劳设计参数。根据文献[1]规定,疲劳设计参数 FD F对于参与总纵强度的甲板上的关键部位的节点取3,而对于其普通部位的节点取2;对于水下浮体的关键部位的节点取5,普通部位的节点取3;但是对难于检测的细节处,关键部位的节点取10,普通部位的节点取5。

对于不确定因素α,当原疲劳损伤数据明确的情况下取1.0,否则取大于1.0的数值。

DP根据(9)式进行计算

式中:TP为已服役的时间;Td为回复期(取为20年);DT为 Td对应的累积损伤。

因此,疲劳强度评估公式为

式中D为剩余服役时间或延寿期内的累积疲劳损伤。

剩余疲劳寿命 TR可按式(11)计算

或按式(12)计算

3 算例

本文算例取某已经服役31年的海洋平台。该平台为八立柱双浮体的半潜式平台。平台设有甲板主体,两个平行的纵向浮筒,连接纵向浮筒的横向浮筒,四角为直径30英尺的立柱,中间为四个直径18英尺的立柱,在立柱与甲板主横梁之间设有撑杆。

3.1 疲劳载荷计算

根据线性势流理论计算疲劳载荷。疲劳载荷计算共划分了1 348个网格,如图1所示。波浪的圆频率ω的范围为0.2,0.4,0.5,0.6,0.7,0.8,0.9,1.0,1.1,1.2,1.3,1.4,1.6,1.8,2.0,共15个频率。

3.2 有限元模型化

图1 水动力计算网格

图2 总体有限元模型

图3 细化有限元模型

有限元模型采用空间的板梁组合结构。骨材尺寸及板厚根据图纸资料及测厚报告而定。其总体有限元模型如图2所示。对于需要进行疲劳校核的局部结构细节,采用t×t的细化有限元网格,本文中的局部细化网格采用内嵌式网格细化方法,即在总体有限元模型中,嵌入细化有限元网格,如图3所示,疲劳校核点如图4所示。

3.3 应力频响函数

将波浪动压力施加到有限元模型上,计算得到结构应力响应。在对计算点的应力进行线性外插得到热点应力后,再虑及板厚修正[1],即可得到计算点的应力频响函数,分别如图5、图6、图7所示。

图4 计算点细化有限元模型

3.4 剩余疲劳强度及剩余疲劳寿命

得到各计算点的应力频响函数后,采用文献[1]中的 E曲线,并采用式(8)及式(11)计算得到各计算点的剩余疲劳强度及剩余疲劳寿命,本例中 FD F取为5,α取为1.5,结果如表1所示。

表1 剩余疲劳强度及剩余疲劳寿命

图5 计算点1应力频响函数

3.5 不确定因素及疲劳设计参数的影响

为了考查不确定因素α及疲劳设计参数 FD F对剩余疲劳强度的影响,本文以节点1为例进行了分析,结果如表2所示。

表2 不确定因素及疲劳设计参数的影响

由表2可知,相对于不确定因素α,疲劳设计参数 FD F对剩余疲劳强度的影响更为明显。为在工程实际中合理评价在役平台结构的剩余疲劳寿命,需要合理确定疲劳设计参数 FD F和不确定因素α。在没有工程经验数据可供参考的情况下,疲劳设计参数FD F可以根据文献[1]规定进行选取,即对参与总纵强度的甲板上的关键部位的节点取3,而对其普通部位的节点取2;对水下浮体的关键部位的节点取5,普通部位的节点取3;但是对难于检测的细节处,关键部位的节点取10,普通部位的节点取5。不确定因素α可以取为1.5。

4 结束语

在役平台结构疲劳强度评估是平台结构安全评估的重要内容之一。本文以某半潜式平台为例,对在役平台结构疲劳强度评估方法进行了研究,得到以下结论:

(1)在役平台结构疲劳强度评估的工程计算法较为简便,是一种对在役平台结构进行疲劳强度评估的有效方法。(2)不确定因素α及疲劳设计参数FD F需要合理确定。在没有工程经验数据可供参考的情况下,可按本文给出的方法进行选取。

[1] American Bureau of Shipping.Rules for building and classing mobile offshore drilling units 2006[S].part 3 hull construction and equipment,2006.

[2] American Bureau of Shipping.Rules for building and classing mobile offshore drilling units 2001[S].part 3 hull construction and equipment,2005.

[3] Det Norske Veritas.Recommended practice DNV-RP-C103:Column-stabilized units[S].2005.

[4] Dean,R G.Relatively Validates of Water Theories[J].Proceedings of ASCE Journal of the Waterways and Harbors Division.1970,96(ww1).

[5] Det Norske Veritas.Classification notes No.30.5:Environmental conditions and environmental loads[S].2000.

[6] American Bureau of Shipping.Guide for buckling and ultimate strength assessment for offshore structure[S].2004.

[7] Journée J M J,Massie W W.Offshore hydromechanics[J].Delft University of Technology,2001.

Engineering Calculation of Structure Fatigue Strength Assessment for Aging Platform Structures

FENG Guo-qing, REN Hui-long, CHEN Bei-yan, Li Hui(Harbin Engineering University,Harbin 150001,China)

P752

B

1001-4500(2010)04-0050-04

2009-12-01; 修改稿收到日期:2010-04-19

冯国庆(1976-),男,博士,副教授。主要从事船舶与海洋工程环境载荷与结构强度评估的研究。