平台导管架波浪拍击计算参数分析

彭绍源, 邓 欣, 尹彦坤, 黄莲英, 邓秀铭

(中海油能源发展油建分公司工程设计研发中心,湛江 524057)

平台导管架波浪拍击计算参数分析

彭绍源, 邓 欣, 尹彦坤, 黄莲英, 邓秀铭

(中海油能源发展油建分公司工程设计研发中心,湛江 524057)

波浪拍击会对平台导管架飞溅区的水平杆件产生近乎垂直的作用力,通过分析这种作用力对结构的影响,并结合工程实例,为工程设计人员更合理地选择设计参数提供参考。

波浪拍击;垂直作用力;设计参数;设计荷载

Abstract:The horizontal circular members in splash zone of an offshore platform jacket may bear vertical loads by wave slamming.This paper presents a method to designers how to select design parameters more felicitously by analyzing the effect on structures and combining the project example.

Key words:wave slamming;vertical loads;design parameters;design loads

0 前言

位于飞溅区的海洋平台导管架的水平杆件会承受波浪拍击力的作用,这些近乎垂直的作用力是由于波浪穿过导管架时,局部水面上升和下降拍击杆件下部所引起的。由于这些力近乎垂直,它们对平台的总体基底剪力和倾覆力矩的作用非常小,但对局部杆件的作用却很大,往往会引起杆件的破坏,所以设计中要特别关注。

波浪拍击力的大小是由作用于杆件上的液体的运动速度变化所引起的,因此它是杆件和自由液面的相对速度的函数。相对拍击速度取决于结构的运动、波高、波浪周期、波浪方向和杆件位置等。

波浪拍击应力计算完毕后,把其与在位计算应力进行组合,以对杆件进行强度校核。

1 波浪拍击的计算公式

管状杆件单位长度的拍击荷载用下列公式计算:

式中:D为杆件直径;ρ为水的密度;u为拍击速度,即杆件与水质点的相对速度,对于海上固定平台的杆件来说,应为水质点的垂直速度;Cs为拍击系数。

2 相关计算参数的选取

2.1 水质点垂直速度 u

以线性波为例,其流场速度势表达式为

因此,可得到其水质点垂直速度为

或者

式(2～4)中:H为波高;T为波周期;ω为波频,ω=2π/T;k为波数,k=2π/L,L为波长;d为水深;g为重力加速度;x为质点水平位置;z为质点垂直位置;t为时间。

由上述表达式可看出:

(1)水质点垂直速度u是波浪相位角kx-ωt的函数。当波浪沿着杆件轴线方向传播时,水质点垂直速度在此方向上呈周期性变化。由于杆件某点出现某一相位的时间是不确定的,所以产生垂直速度最大值时所对应的杆件位置以及波浪对杆件的拍击作用也是不确定的。

当波浪垂直于杆件轴线方向传播时,同一相位(时刻),杆件轴线方向上每一点的水质点垂直速度都是相同的。在半个波浪周期内,水质点垂直速度的最大值总会出现一次。

在实际工程中,可不考虑波浪的传播方向,并且按照杆件轴线方向上水质点的垂直速度都等于其最大值,即为线性均布荷载来计算。

(2)水质点的垂直速度u是水深d的函数,即波浪在不同的水深条件下将产生不同的水质点垂直速度。在作导管架整体计算时,采用的水位一般包括极端低水位、极端高水位、最低天文潮和最高天文潮。与之相一致,在计算水质点垂直速度时,可将水深 d在最小值(对应极端低水位)和最大值(对应极端高水位)之间调整,以得到最大速度。

在实际工程中,可只选取四个水位(极端低水位、极端高水位、最低天文潮和最高天文潮)进行水质点垂直速度的计算,选取最大值即可。

由于用于整体计算的软件SACS带有计算质点的速度和加速度的功能,因此,拍击速度可以直接从SACS的计算结果中选取。

2.2 拍击系数Cs

波浪拍击系数Cs由试验确定。由于各学者的试验条件与方法不同,其得到的结果差别较大。综合Dalton和Nash(1976)、Mill(1977)、Sarpkaya(1978)、Isaacson和Prasad(1993)等学者的研究成果,Cs的取值范围为0.5～7.79。

Sarpkaya(1978)指出系数 Cs的经验值是它的理论值π的0.5～1.7倍,它取决于水的上升时间和弹性安装的杆件自振频率。Sarpkaya和Isaacson建议,如果进行动力响应分析,可以使用理论值 Cs=π,否则应取 Cs=5.5。对于光滑圆截面杆件,Cs应不小于3.0[1]。

因此,在实际工程中,对杆件进行强度分析时,可取 Cs=5.5。

2.3 杆件有效直径 De和拍击直径Ds

在计算杆件惯性矩 I或抗弯模量W时,所用的杆件直径应当为有效直径De(由杆件直径D的基础上剔除腐蚀和裂纹厚度后得到)。如图1所示,杆件腐蚀最大厚度为 Tcor,裂纹最大厚度为 Tcrk,则有效厚度为 Te=T-max(Tcor,Tcrk),有效直径为De=D-2Te。上述计算公式是基于最大腐蚀或裂纹厚度贯通于整根杆件而假定的。

公式(1)中的杆件直径应当为拍击直径Ds。实际上,由于腐蚀和裂纹可能只发生在杆件的局部,杆件受波浪拍击作用范围的减小量并不明显,因此可以假定拍击直径 Ds不受腐蚀和裂纹的影响。另一方面,应当考虑海生物附着、附属构件等对杆件作用范围的影响,因此,拍击直径应在杆件直径D的基础上等效增大。

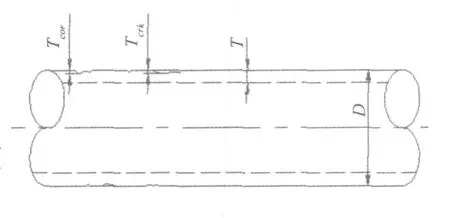
图1 杆件裂纹和腐蚀示意图

2.4 杆件有效长度Le

由公式(1)计算的拍击荷载为线荷载,要计算杆件的弯矩,还应确定杆件的有效长度Le。由于拍击荷载是垂向的,因此只有在立面上的斜撑才对水平杆件产生有效支撑作用。如图2所示,斜撑 DC、EC对水平杆件AB产生支撑作用。因此,水平杆件 AB可以分为A C和CB两段分别进行计算,其有效长度分别为AC和CB的长度。

而在平面上的斜撑并不产生作用。如图3所示,斜撑DC、EC对水平杆件AB不产生支撑作用(理论上说,是有一定作用的,但在实际工程中,可不予考虑)。因此AB的有效长度即为AB的实际长度。

2.5 杆件端部约束形式

杆件端部约束形式影响以下两个参数:

(1)杆件的自振周期。根据理论计算公式,杆件的自振周期会影响拍击系数Cs,但如前文所述,Cs值可依照经验选取,杆件自振周期(以至杆件端部约束形式)不需再考虑。

(2)杆件的最大弯矩。不同约束条件下,承受同样荷载的杆件的最大弯矩及最大弯矩出现的位置是不同的。由于导管架水平杆件的端部与腿柱焊接连接,可假定杆件约束条件为两端固定。当考虑导管架立面斜撑的作用时,如图2中的杆件 AC和CB,由于 C点受到较大的垂向约束,也可以假定上述两杆件约束条件为两端固定。

图2 立面支撑示意图

3 波浪拍击应力与在位应力组合

相关参数确定后,可计算出沿杆件轴线方向上各点的波浪拍击应力。同时,从SACS程序的整体计算结果中可以查看该杆件各点上的在位应力,把此二项应力进行组合,即可得到杆件最大应力及其出现的位置。

在实际工程中,可以假定在沿杆件轴线方向的各点上,波浪拍击应力和在位应力均为其最大值,组合时把二者直接叠加即可。

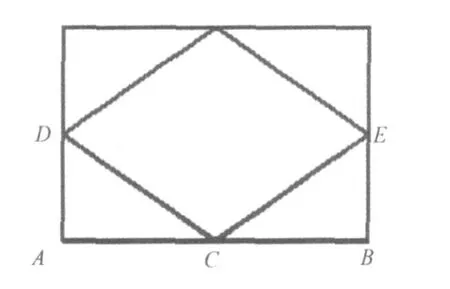
图3 平面支撑示意图

4 工程实例

以涠洲11-1N井口平台导管架飞溅区的一水平杆件为例,对其进行波浪拍击计算。平台位置水深为37.2 m,极端低水位为-0.44 m,极端高水位为+5.70 m,最低天文潮位为±0.00 m,最高天文潮位为+5.23 m。

波浪和海流的极值如下表1、表2所示。

表1 涠洲11-1N油田波浪的极值

表2 涠洲11-1N油田海流的极值

极端高水位和极端低水位对应100年一遇的波流条件,最高天文潮和最低天文潮水位对应1年一遇的波流条件。

采用流函数理论,利用SACS程序进行计算,得到各水位条件下,水质点由海底到水面范围内不同高度和不同相位的垂直速度。

该平台导管架处于飞溅区的水平杆件标高为+6 m,则其与海底垂直距离为 d=37.2+6=43.2 m。根据SACS程序的计算结果,该处水质点速度最大值对应的水位为极端高水位,其值为 u=3.5514 m/s。

选取的水平杆件截面尺寸为 Ф610 mm×19 mm,长度为15 m,考虑7.5 mm的腐蚀厚度后,截面有效尺寸为Ф595 mm×11.5 mm;考虑走道、栏杆等附属杆件对拍击荷载的影响(该处无海生物附着),拍击直径Ds等效增大至900 mm,则:

杆件单位长度的拍击荷载Ws=0.5ρCsDsu2=0.5×1.025×5.5×0.9×3.55142=31.9962 kN/m;最大弯矩 Mmax=Ws×L2e/12=31.9962×152/12=599.93 kN·m;抗弯截面模量W=π×(D4e-d4e)/(32D)=3.141×[0.5954-(0.595-0.0115×2)4]/(32×0.595)=0.0030 m3;拍击应力 fb=Mmax/W=599.93/(0.0030×1 000)=198.86 MPa;根据文献[1],由管径与壁厚的比值 De/Te,查到允许弯曲应力的表达式,在极端工况下允许弯曲应力可以提高到1.33倍,Fb=355×0.84×1.33=397.5 MPa,则拍击应力系数为fb/Fb=198.86/397.5=0.50。

由在位计算结果得知,该杆件最大在位应力系数为0.39。把此二项系数组合得0.50+0.39=0.89<1.0,杆件满足强度要求。

5 结束语

本文对波浪拍击的相关参数的选取进行了分析,并结合海洋工程的实际需要,作了一些偏于保守的简化和假定。应该说,按照此法对波浪拍击进行计算的结果是可靠的。但如通过计算,发现一些杆件不能满足强度要求,则可考虑对相关参数进行更加详尽的分析和调整,以更合乎实际需要。

[1] 中华人民共和国石油天然气行业标准SY/T 10030-2004,海上固定平台规划、设计和建造的推荐作法——工作应力法[S].中华人民共和国国家发展和改革委员会,2004.

[2] 中华人民共和国石油天然气行业标准SY/T 10050-2004,环境条件和环境荷载规范[S].中华人民共和国国家发展和改革委员会,2004.

[3] Miller B L.Wave slamming loads on horizontal circular elements of offshore structures[J].Naval Archi,1978,3:81-92.

[4] Sarpkaya T.Wave impact loads on cylinders[C].Proceedings of Offshore Technology Conference,1978,169-176.

[5] Kaplan P,Silbert M N.Impact force on platform horizontal members in the splash zone[C].Proceedings of Offshore Technology Conference,1976,749-758.

[6] Garrison C J.Wave impact loads on circular structure members[J].Applied Ocean Research,1996,18(1):45-54.

[7] Hariprasad V,Sundaravadivelu R,Neelamani S.Slamming forces due to random waves on horizontal circular members in intertidal zone[C].Civil Engineering in The Oceans VI.

[8] Michael I,Kesavan S.Random wave slamming on cylinders[J].Journal of Waterway,Port,Coastal and Ocean Engineering,1990,116(6):742-763.

[9] Suchithra N,Koola P M.A study of wave impact on horizontal slabs[J].Ocean Engineering,1995,22(7):687-697.

[10] Offshore Standard DNV-OS-J101.Design of offshore wind turbine structures[S].2004.

[11] 李远林.近海结构水动力学[M].广州:华南理工大学出版社,1999.

[12] 苏翼林.材料力学[M].天津:天津大学出版社,2003.

Parameters Analysis for Calculation of Wave Slamming on Platform Jackets

PENG Shao-yuan, DENG Xin, YIN Yan-kun, HUANG Lian-ying, DENG Xiu-ming
(Research&Development Center,Field Construction Engineering Co.,CNOOC,Zhanjiang 524057,China)

TE53

A

1001-4500(2010)04-0032-04

2010-03-15; 修改稿收到日期:2010-06-12

彭绍源(1982-),男,工程师,主要从事海洋工程结构设计。