秦香止泻片半成品及成品吸湿性研究

赵碧清，何群，滕久祥，彭芝配，史艳霞

(湖南中医药大学药学院，湖南长沙 410208)

秦香止泻片半成品及成品吸湿性研究

赵碧清，何群，滕久祥*，彭芝配，史艳霞

(湖南中医药大学药学院，湖南长沙 410208)

秦香止泻片;干浸膏粉;素片;薄膜包衣片;吸湿速度;相对湿度

目的:对秦香止泻片的干浸膏粉、素片及薄膜包衣片的吸湿性进行研究。方法:通过测定秦香止泻片的干浸膏粉、素片、薄膜包衣片的吸湿速度，含水量达3%时的相对湿度(RH)，建立其动力学模型，提取吸湿速度参数并比较大小。结果:秦香止泻片的干浸膏粉、素片的吸湿动力学模型符合Higuchi方程，而其薄膜包衣片的吸湿动力学模型符合零级动力学模型。操作环境的相对湿度应控制在78%以下，才能有效防止吸湿或裂片。结论:包薄膜衣可使秦香止泻片的干浸膏粉吸湿速度减慢。

秦香止泻片来源于本院著名中医内科专家滕久祥教授研制的治疗湿热痢疾的临床经验方，由秦皮、木香等四味中药材组成，具有良好的行气止痛、健脾消食之功效，多用于胸脘胀痛、泻痢后重、食积不消等症［1］。本方药材经水提得到的干浸膏粉易吸湿，为了掌握本制剂的干浸膏粉、素片、包衣片的吸湿特性，从而确定生产过程中各道工序、每步操作环节的湿度条件，控制生产环境的相对湿度(RH)，笔者取一批中试样品(批号070108)生产过程中的半成品(干浸膏粉、素片)及成品(包衣片)，在相同条件下研究了其吸湿特性，为工业化生产提供了实验依据。

1 仪器与试药

MA110型电子分析天平(上海市第二天平仪器厂);ZK-82A真空干燥箱(上海市实验仪器总厂);超声波清洗器(北京医疗设备二厂);SHH-150L生化培养箱(重庆四达实验仪器有限公司);五氧化二磷等所用试药、试剂均为分析纯。

2 方法与结果

2.1 吸湿速度的研究

2.1.1 吸湿速度的测定方法［2］按比例称取一定量的各试验样品，置于五氧化二磷干燥器内干燥72 h至恒重。将底部盛有氯化钠过饱和溶液的干燥器放于25℃恒温培养箱内恒温24 h，此时干燥器内的相对湿度为75%。在已恒重的称量瓶底部放入厚约2 mm的样品，准确称重后置于干燥器内(称量瓶盖打开)于25℃保存，定时(3、6、12、24、48、60、72、 84 h)，称量，按下式计算吸湿百分率，并以吸湿百分率为纵坐标，时间(h)为横坐标作图，建立吸湿速度的数学模型，求吸湿速度参数，从而确定生产、贮存过程中空气湿度的控制范围及操作条件。吸湿百分率(Y%)=(吸湿后样品重量－吸湿前样品重量)/吸湿后样品重量×100%。

2.1.2 各试验样品吸湿速度测定结果见表1，图1。

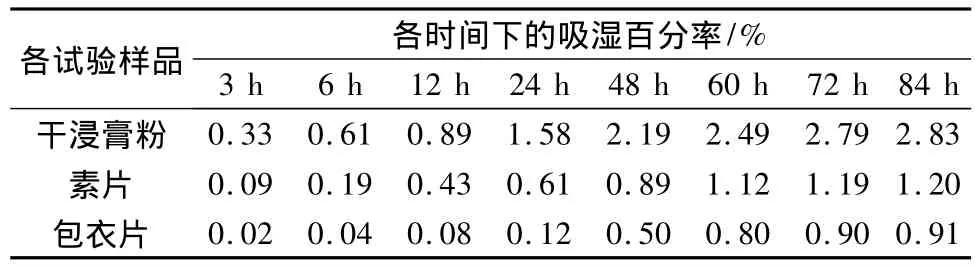
表1 各试验样品吸湿速度测定结果

图1 各试验样品吸湿速度曲线

2.1.3 建立各试验样品吸湿速度曲线的动力学模型［3］对秦香止泻片的干浸膏粉、素片、包衣片测定的吸湿百分率随时间变化规律的函数关系采用几种接近的数学模型进行拟合(DPS统计软件复核)，每个实验样品比较各自的拟合度R2、方差F、显著性P，找出可行的、最接近的数学模型，确定为该种实验样品吸湿速度的动力学模型，结果见表2。

表2 试验样品吸湿速度动力学模型拟合R2、F、P值

由表2可知:4种可行的数学模型中，干浸膏粉、素片最接近Higuchi方程(R2值愈大、F值愈大、P值愈小则愈接近相对应的数学模型)，干浸膏粉、素片2组试验样品的吸湿速度动力学方程皆属Higuchi方程。Higuchi方程的数学表达式为:Y= bt1/2+a，Y为吸湿百分率，t为时间，b为吸湿速度动力学方程斜率，a为吸湿速度动力学方程截距。而包衣片最接近零级模型，即零级模型为包衣片最优吸湿速度模型，其数学表达式为:Y=bt+a，Y为吸湿百分率，t为时间，b为吸湿速度动力学方程斜率，a为吸湿速度动力学方程截距。

2.1.4 提取各试验样品吸湿百分率为1%所需要的时间t1%，并求出误差范围(95%置信区间Z)将Y=1%时，代入各试验样品对应的动力学方程，求出各自的t1%，再根据理论值t 95%可信限的置信区间t1%±Z，其中Z用DPS统计软件计算，按稳定性试验技术要求，试验结果应取下限，结果见表3。

表3 各试验样品动力学方程、t1%±z数据

从表3计算结果可知，干浸膏粉组、素片组、包衣片组每两组间误差范围均没有重叠，差别有统计意义，说明干浸膏粉压成素片后可明显降低本品的吸湿性，尤其是素片包肠溶薄膜衣后更加显著地降低本品的吸湿性。各试验样品吸湿百分率为1%所需时间t1%，按药物稳定性技术要求，应取下限，所以在成型工艺过程中，若温度为25℃，RH为75%时，干浸膏粉、素片、肠溶薄膜包衣片分别暴露于空气中12.62、54.38、65.50 h时吸湿百分率可达1%。本试验结果可为大生产提供参考，以防产品生产过程中暴露时间过长吸湿潮解，影响质量。

2.2 生产中控制湿度的测定

2.2.1 吸湿百分率与相对湿度函数曲线的测定在已恒重的称量瓶底部分别放入适量干燥至恒重的待测样品，准确称量后分别置于表4中所列的盛有7种不同浓度硫酸和不同盐的过饱和溶液的干燥器内(称量瓶盖打开)，于25℃恒温培养箱中保持7 d后称重，计算吸湿百分率，结果见表4，图2。

2.2.2 建立吸湿百分率随相对湿度变化曲线的动力学模型对干浸膏粉、素片、包衣片吸湿百分率随相对湿度变化规律的函数关系采用几种接近的数学模型进行拟合(DPS统计软件处理)，每个湿度下试验样品比较各自的拟合度R2、方差F、显著性P，找出可行的、最接近的数学模型，确定为该试验样品吸湿百分率随相对湿度变化函数关系的数学方程，结果见表5。

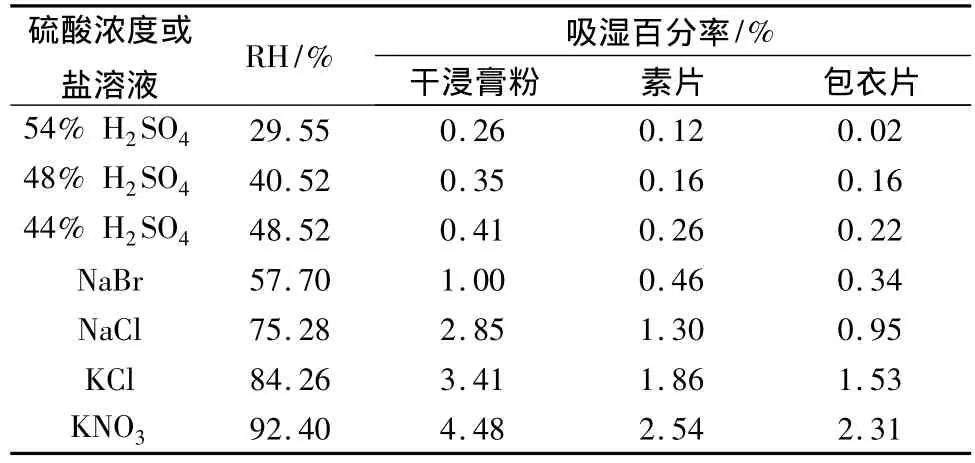
表4 不同相对湿度条件下各试验样品的吸湿百分率

图2 不同相对湿度条件下各试验样品的吸湿百分率

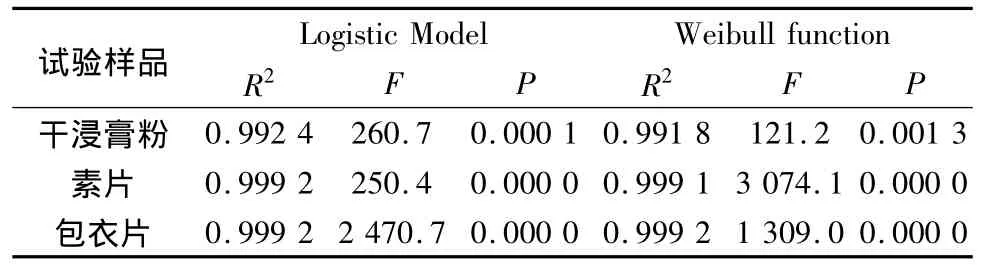
表5 试验样品吸湿百分率随相对湿度变化函数关系的数学模型拟合

由表5可知:2种可行的数学模型中，干浸膏粉、素片、包衣片最佳数学模型均为逻辑斯蒂模型(Logistic Model)，其表达式为:Y=C1/［1+exp(C2+C3X)］，Y表示吸湿百分率，X表示相对湿度。将Y=3%，代入公式计算对应的相对湿度，结果见表6。

即干浸膏粉、素片、包衣片含水量达3%时对应的相对湿度分别为78.38%、98.40%、97.98%。

表6 含水量达3%时对应的相对湿度计算结果

由此可知:制粒、压片、包衣、包装等各工序的生产及贮存环境的相对湿度应控制在干浸膏粉、素片、包衣片含水量达3%时对应的相对湿度以下，即操作环境的相对湿度应控制在78%以下，才能有效防止干浸膏粉吸湿，导致压片时黏冲。

3 讨论

3.1 中药干浸膏粉为多种组分的混合物，吸湿性强，制备固体制剂过程中环境的相对湿度、各道工序半成品、成品暴露空气中的时间、温度等因素直接影响到制剂的质量，如:混合、制粒、压片、包衣、分剂量、包装，尤其是对产品稳定性，影响最大，它是整个成型工艺的关键，必须通过实验求出合理的相对湿度、放置时间等湿度参数，确定最佳的湿度条件。

3.2 由实验结果可知:温度为25℃，RH为75%时，干浸膏粉、素片、包衣片吸湿百分率达1%所需时间分别为12.62、54.38、65.50 h，故生产中应控制各道工序半成品、成品暴露空气中的时间，尽量缩短操作时间。

3.3 临界相对湿度(CRH)是水溶性药物一个特征的参数［4］，而中药颗粒一般为混合物，类似于水不溶性药物，吸湿曲线为一连续函数，无明显的临界相对湿度(CRH)，再加上实验中存在取点误差，所以不能采用两点切线法求出临界相对湿度。根据中药片剂干颗粒含水量一般在3%～5%，而本制剂为全浸膏片，含水量大于3%时制粒黏筛网、压片黏冲、素片及包衣片黏手，故取含水量为3%时对应的相对湿度(有意义的相对湿度)作为生产中的控制指标(类似于临界相对湿度)，以防止干浸膏粉吸湿，制粒困难，或导致压片时黏冲;素片吸湿导致崩解剂膨胀裂片;包衣片吸湿导致衣膜变软破裂，保证成品质量稳定。

3.4 受实验条件限制，未考察不同温度、不同相对湿度条件下各半成品、成品的吸湿速度，从而获得更多的湿度参数，这是本文的不足，须完善之。

致谢:数理教研室刘明芝教授对本文统计学处理给予的指导及帮助。

［1］雷截权.中药学［M］.上海:上海科学技术出版社，1995:64.

［2］何群，李万忠，王净浄，等.不同辅料对愈痫灵颗粒所用原料(干膏粉)吸湿性的影响［J］.中国药学杂志，2007，42(10): 753-757.

［3］刘明芝.中医药统计学［M］.1996.

［4］陆冰.固体制剂吸湿性研究进展(上)［J］.中国药师，2007，10(5):445-447.

R944

A

1001-1528(2010)05-0770-03

2009-11-18

湖南省教育厅重点项目(05A0312)

赵碧清(1972－)，女，副教授，研究方向为中药新药制备工艺与质量标准。E-mail:qingerhn@126.com

*通讯作者:滕久祥(1947－)，男，教授，博士导师，主要从事中医内科老年病临床研究及中药新药开发研究工作。Tel:(0731)85381088