Wm与Pn(n≤3)联图的点可区别边色数＊

王国兴

(兰州商学院信息工程学院,甘肃兰州730020)

Wm与Pn(n≤3)联图的点可区别边色数＊

王国兴

(兰州商学院信息工程学院,甘肃兰州730020)

设G是简单图,图G的一个k-点可区别正常边染色f是指一个从E(G)到{1,2,…,k}的映射,且满足∀u,v∈V(G),u≠v,有S(u)≠S(v),其中S(u)={f(uw)|uw∈E(G)}.数min{k|G存在k-VDPEC染色}称为图G的点可区别正常边色数,记为研究了Wm∨Pn(n≤3)的点可区别边染色,给出了Wm∨Pn(n≤3)的点可区别边色数.

联图;点可区别边染色;点可区别边色数

图的染色问题是图论研究的主要内容之一.图的染色的基本问题就是确定其各种染色法的色数.Burris, Schelp等人提出点可区别边染色的概念,得到了若干结果,并提出了有关猜想[1～3].文献[4～7]研究了一些图的点可区别正常边染色.本文给出了点Wm∨Pn(n≤3)可区别正常边染色.

1 预备知识

定义1[1～3]设f是图G的一个使用了k种色1,2,…,k的正常边染色,对任意的u∈V(G)记S(u)= {f(uw)|uw∈E(G)},称S(u)为点u在f下的色集合.并且记(u)={1,2,…,k}S(u).如果对∀u,v∈ V(G),u≠v,有S(u)≠S(v),那么称f是图G的一个k-点可区别正常边染色,简记为k-VDPEC,且称(G)=min{k图G存在k-VDPEC}为G的点可区别正常边色数.

若S(u)≠S(v),则称u与v是可区别的.显然给出G的一个正常边染色之后,为证它是点可区别的,只需说明任意两个同度点可区别即可.显然,图G存在点可区别正常边染色当且仅当G没有孤立边且最多有一个孤立点.

对图G,令nk表示度为k的顶点个数,δ≤k≤Δ,设

猜想[1～3]若G是没有孤立边并且最多有一个孤立点的图,则(G)或μ(G)+1.

定义[8]设G和H是点不相交且边不交的简单图,V(G∨H)=V(G)∪V(H),E(G∨H)=E(G)∪E(H)∪{uv|u∈V(G),v∈V(H)},则称G∨H是G与H的联图.引理1[1]对n≥3的n阶完全图Kn,有

本文中总记m+1阶的轮Wm的顶点集为V(Wm)={ui|i=0,1,…,m},边集为E(Wm)={u0ui|i=1,…, m}∪{uiui+1|i=1,…,m-1}∪{umu1}.记n阶的路Pn的顶点集为V(Pn)={vj|j=1,2,…,n},边集为E (Pn)={vjvj+1|j=1,2,…,n-1}.

2 主要结论

定理1 当m≥3时,

证明 分以下两种情况考虑.

情形1 当m=3时,W3∨P1=K5,由引理1知结论成立,即

1)当m=4时,给出W4∨P1的一个使用了颜色为1,2,3,4,5,6的边染色如下:

u0u1,u0u2,u0u3,u0u4依次用2,3,4,5去染;v1u1,v1u2,v1u3,v1u4,依次用1,2,3,4去染;v1u0用6去染; u1u2,u2u3,u3u4,u4u1依次用4,6,1,6去染.

对上述染色,有S(u1)={1,2,4,6},S(u2)={2,3,4,6},S(u3)={1,3,4,6},S(u4)={1,4,5,6}, S(u0)={2,3,4,5,6},S(v1)={1,2,3,4,6}.因此,上述染色是W4∨P1的使用了6种色点可区别正常边染色.

2)当m>4时,给出Wm∨P1的一个使用了颜色为1,2,…,m+2的边染色如下:

u0u1,u0u2,…,u0um依次用2,3,…,m+1去染;v1u1,v1u2,…,v1um依次用1,2,3,…,m去染;v1u0用m+ 2去染;u1u2,u2u3,…,um-1um,umu1依次用4,5,6,…,m+2,3去染.

对上述染色,有S(u0)={2,3,…,m,m+2},S(ui)={i,i+1,i+2,i+3},i=1,2,…,m-1.

S(um)={3,m,m+1,m+2},S(v1)={1,2,…,m,m+2}.

综合上述染色两种情况,定理1为真.

定理2 当m≥3时,

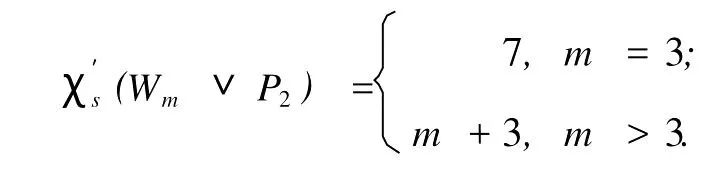
证明 分以下两种情况考虑.

情形1 当m=3时,W3∨P2=K6,由引理1知结论成立,即

1)当m=4时,给出W4∨P2的一个使用了染色为1,2,3,4,5,6,7的边染色如下:

u1u2,u2u3,u3u4,u4u1依次用1,2,3,7去染;v1u1,v1u2,v1u3,v1u4依次用2,3,4,5去染;v2u1,v2u2,v2u3, v2u4依次用3,4,5,6去染;u0u1,u0u2,u0u3,u0u4依次用4,5,6,1去染;u0v1,u0v2,v1v2依次用7,2,1去染.

对上述染色,有S(u1)={1,2,3,4,7},S(u2)={1,2,3,4,5},S(u3)={2,3,4,5,6},S(u4)={1,3,5, 6,7},S(u0)={1,2,4,5,6,7},S(v1)={1,2,3,4,5,7},S(v2)={1,2,3,4,5,6}.

2)当m=5时,给出W5∨P2的一个使用了颜色为1,2,3,4,5,6,7,8的边染色如下:

u1u2,u2u3,u3u4,u4u5,u5u1依次用1,2,3,8,5去染;v1u1,v1u2,v1u3,v1u4,v1u5依次用2,3,4,5,6去染; v2u1,v2u2,v2u3,v2u4,v2u5依次用3,4,5,6,7去染;u0u1,u0u2,u0u3,u0u4,u0u5依次用6,7,8,4,3去染;u0v1, u0v2,v1v2依次用1,2,8去染.

3)当m≥6时,给出Wm∨P2的一个使用了颜色1,2,…,m+2,m+3的边染色如下:

u1u2,u2u3,…,um-1um,umu1依次用1,2,3…,m-1,m去染;u0u1,u0u2,…,u0um依次用4,5,…,m+3去染;v1u1,v1u2,…,v1um依次用2,3,…,m+1去染;v2u1,v2u2,…,v2um依次用3,4…,m+2去染;u0v1,u0v2, v1v2依次用1,2,m+3去染.

因此,上述染色是点可区别正常边染色,所以m>3当时

综合上述染色两种情况,定理2为真.

定理3 当m≥3时,

证明 当m≥3时,有

μ(Wm∨P3)

分以下五种情况考虑.

情形1 当m=3时,μ(W3∨P3)

下面给出W3∨P3的一个使用了颜色为1,2,3,4,5,6,7的边染色如下:

u1u2,u2u3,u3u1依次用1,2,3去染;u0u1,u0u2,u0u3依次用2,3,4去染;v1u1,v1u2,v1u3依次用4,5,6去染;v2u1,v2u2,v2u3依次用5,6,7去染;v3u1,v3u2,v3u3依次用6,7,1去染;u0v1,u0v2,u0v3依次用7,1,5去染; v1v2,v2v3依次用3,4去染.

S(v2)={2},S (v3)={2,3}.

情形2 当m=4时,μ(W4∨P3)

下面给出W4∨P3的一个使用了颜色为1,2,3,4,5,6,7,8的边染色如下:

u1u2,u2u3,u3u4,u4u1依次用1,2,3,4去染;u0u1,u0u2,u0u3,u0u4依次用7,3,4,5去染;v1u1,v1u2,v1u3, v1u4依次用3,4,5,6去染;v2u1,v2u2,v2u3,v2u4依次用5,6,7,8去染;v3u1,v3u2,v3u3,v3u4依次用6,7,8,2去染;u0v1,u0v2,u0v3,v1v2,v2v3依次用8,2,1,1,3去染.

情形3 当m=5时,μ(W5∨P3)

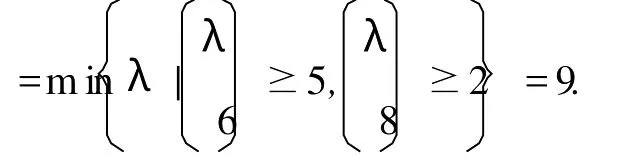
下面给出W5∨P3的一个使用了颜色为1,2,3,4,5,6,7,8,9的边染色如下:

u1u2,u2u3,u3u4,u4u5,u5u1依次用1,2,3,4,5去染;u0u1,u0u2,u0u3,u0u4,u0u5依次用8,9,4,5,6去染; v1u1,v1u2,v1u3,v1u4,v1u5依次用3,4,5,6,7去染;v2u1,v2u2,v2u3,v2u4,v2u5依次用4,5,6,7,8去染;v3u1, v3u2,v3u3,v3u4,v3u5依次用6,7,8,9,1去染;u0v1,u0v2,u0v3,v1v2,v2v3依次用2,1,3,9,2去染.

情形4 当m=6时,μ(W6∨P3)

下面给出W6∨P3的一个使用了颜色为1,2,3,4,5,6,7,8,9,10的边染色如下:

u1u2,u2u3,u3u4,u4u5,u5u6,u6u1依次用1,2,3,4,5,6去染;u0u1,u0u2,u0u3,u0u4,u0u5,u0u6依次用8,3, 4,5,6,7去染;v1u1,v1u2,v1u3,v1u4,v1u5,v1u6依次用3,4,5,6,7,8去染;v2u1,v2u2,v2u3,v2u4,v2u5,v2u6依次用4,5,6,7,8,9去染;v3u1,v3u2,v3u3,v3u4,v3u5,v3u6依次用6,7,8,9,10去染;u0v1,u0v2,u0v3,v1v2,v2v3依次用1,10,2,2,1去染.

情形5 当m≥7时,给出Wm∨P3的一个使用了颜色为1,2,…,m+3,m+4的边染色如下:

u1u2,u2u3,u3u4,…,um-2um-1,um-1um,umu1依次用1,2,3,…m-2,m-1,m去染;u0u1,u0u2,…,u0um-1, u0um依次用5,6,…,m+3,m+4去染;v1u1,v1u2,…,v1um-1,v1um依次用2,3,…,m,m+1去染;v2u1,v2u2,…,v2um-1,v2um依次用3,4,…,m+1,m+2去染;v3u1,v3u2,…,v3um-1,v3um依次用4,5,…,m+2,m+3去染,u0v1,u0v2,u0v3,v1v2,v2v3依次用1,2,3,m+4,1去染.

综合上述五种情况,有S(u)≠S(v),对∀u,v∈V(Wm∨P3),u≠v,所以上述所给染色是Wm∨P3的使用了m+4种色的点可区别正常染色.即有

定理3为真.

[1]BurrisA C,Schelp R H.Vertex-distingguishing proper edge-coloring[J].J of Graph Theory,1997,26(2):73-82.

[2]Bazgan C,Harkat-Benhamdine A,Li H,et al.On the Vertex-distinguishing proper edge-coloring[J].Combin Theory SerB, 1999,75(2):288-301.

[3]Balister P N,BollobasB,Shelp R H.Vertex-distinguishing coloring of graph with 2[J].Discrete Mathematics,2002,252(2): 17-29.

[4]Zhang Zhongfu,liu Linzhong,Wang Jianfang.Adiacent strong edge coloring of graph[J].Applied Mathematics Letters,2002,15 (5):623-626.

[5]王国兴.Wm∨C3的点可区别正常边色数[J].佳木斯大学学报:自然科学版,2010,28(1):144-145.

[7]陈祥恩,张忠辅.K-tn的点可区别正常边染色[J].数学研究,2004,37(4):376-380.

[8]Bondy J A,MurtyU S R.Graphs theorywith application[M].New York:TheMacmlllan PressLtd,1976.

Vertex D ist inguishing Edge Chromatic Numbers of the Jo in of the GraphsWmand path Pn(n≥3)

WANG Guo-xing

(School of Information Engineering,Lanzhou University of Finance and Economics,Lanzhou Gansu 730020,China)

LetGbe a simple graph.An nor mal coloringfofGrefers to a coloring of the vertices ofGso that no two adjacent vertices receive the same color.LetS(u)be the set of colors of vertex incident to u underf.For An normal coloringfofGusingk-colors,ifS(u)≠S(v)for any two different verticesuandvofV(G),thenfis called ak-VDPEC coloring ofG.The min imum number of colors required for a VDPEC coloring ofGis denotedand it is called the VDPEC chromatic numbers ofG.Vertex distinguishing proper edge colorings of the join ofwheelWmand pathPn(n≥3)are studied and the vertex distinguishing edge chromatic numbers of the join ofwheelWmand pathPn(n≥3)are obtained in this paper.

the join of graphs;vertex-distinguishing proper edge coloring;ver-distinguishing proper edge chromatic number

book=9,ebook=358

O 157.5

A

1673-2103(2010)05-0019-05

2010-06-24

王国兴(1976-),男,甘肃天水人,讲师,硕士,研究方向:图论及其应用.