硅基超晶格Si1－xSnx/Si的能带结构

吕铁羽陈捷 黄美纯

(厦门大学物理系，厦门361005)

(2009年10月23日收到)

硅基超晶格Si1－xSnx/Si的能带结构

吕铁羽†陈捷 黄美纯

(厦门大学物理系，厦门361005)

(2009年10月23日收到)

由于Si基发光材料能与现有的Si微电子工艺兼容，其应用前景被广泛看好.设计具有直接带隙的Si基材料，备受实验和理论研究者的关注.本文根据芯态效应、电负性差效应和对称性效应设计了Si基超晶格Si1－xSnx/Si.其中Si0.875Sn0.125/Si为直接带隙材料.在密度泛函框架内，采用平面波赝势法计算表明，Si0.875Sn0.125/Si为直接带隙超晶格，最小带隙在Γ点.进一步采用准粒子近似方法计算，我们预测该材料的带隙值为0.96 eV.

密度泛函，准粒子近似，Si基超晶格

PACC:6185，7115H

1. 引言

众所周知，Si是一种间接带隙半导体材料，它的禁带宽度约为1.17 eV，价带顶在Γ点，导带底在Γ-X方向上的X点附近(约85%处).由于动量守恒的要求，电子的间接跃迁必须借助于其他准粒子过程，如声子的参与，其跃迁概率远小于直接跃迁.因此，体Si不是一种合适的发光材料，直接在Si材料上实现全Si光电子集成是一件几乎不可能的事情.于是，多年来世界上许多科学家把注意力集中到Ⅲ-Ⅴ及Ⅱ-Ⅵ族化合物这些直接带隙材料上，将其作为一种重要的光电子材料和器件，研究它们与Si芯片的兼容性问题.虽然已经获得某些进展，但是由于化合物材料的极性晶面，在Si上生长及长期稳定性都是一个严峻的挑战.此外，由于Si的资源丰富、价格低廉、纯度高，加上Si平面工艺成熟精细，它将是目前相当长时间内不可替代的微电子材料.因此，Si基发光材料的研究具有重要的意义.

近年来对Si基材料的研究表明，Si不发光的性质有可能被改变［1—7］.然而，在这些方案中，Si基材料或器件的发光过程多数与界面有关，这使光响应速度不能满足超高速信息技术的要求.于是直接把Si的间接带隙改造成为直接带隙的Si基新材料研究便成为一项非常具有挑战性的工作.

能带理论告诉我们，如果能够人工设计出具有直接带隙特征的Si基新材料，发光效率及光响应速度的问题将有可能同时得到很好的解决.最近，由黄美纯教授等［8—10］总结出的对称性降低原则将可能成为设计直接带隙半导体的重要原则之一.

由于局域密度近似(LDA)是基于基态的理论，对材料激发态性质的预测总是不令人满意.而准粒子近似(GWA)方法［11，12］是适用于激发态性质的计算，大量的报道显示，对于sp系统，该方法预测的带隙值与实验值之间的误差在0.1 eV之内［13，14］.我们希望通过GWA方法准确预测Si1－xSnx/Si超晶格的带隙值.但是GWA方法的计算量很大，要求的计算时间和资源(如内存)随着系统的增大呈指数阶增长.所以，在本文中我们只针对Si0.875Sn0.128/Si超晶格做GWA计算.

2. 理论和方法

鉴于实际半导体材料的多体复杂性，不仅其电子结构没有解析解，决定其带隙类型的因素也不可能有严格可靠的解析理论.黄美纯教授综合分析了50多种最常见的半导体材料的能带结构参数，包括元素半导体、化合物半导体以及一些新的半导体材料，提出决定带隙类型的主要因素有三个，即芯态效应、原子的电负性差效应和晶体对称性效应［15］.实际上这三个效应都是作用在价电子上的晶体有效势的重要组成部分.

2.1. 芯态效应

材料的能带结构与晶格常数存在密切的关系.即便是同一种材料，晶格常数增大最敏感的效应是Γ导带底能量的迅速降低.而实现在常温常压下增大晶格常数的有效方法是选择芯态较大的原子来替代.

2.2. 电负性差效应

对于化合物半导体，组成晶体的两种原子之间存在所谓极性键，它与原子间的电负性差直接相关.在赝势理论中，它表现为势的反对称部分.观察GaSb，GaAs，GaP，InSb和AlSb的能带结构，发现Γ导带底的能量随电负性的减小而迅速向Γ价带顶靠近，使GaSb，GaAs和InSb成为直接带隙半导体，而电负性较大的GaP和AlSb为间接带隙材料.虽然目前还没有理论能够定量说明这个变化规律，而且我们注意到用别的(如Phillips)电负性标度，其变化规律就不如此明显.但是，半导体导带底能量在Pauling电负性标度下的这一变化趋势仍然可以作为设计直接带隙材料的借鉴.

2.3. 对称性效应

AlN与AlSb，GaN与GaP比较，AlN和GaN的电负性差较大，芯态较小.但是AlN和GaN是直接带隙半导体.造成这种现象的一个重要原因是它们的晶体对称性.降低晶体对称性，即减少对称点群的操作数，有利于设计和合成具有直接带隙的半导体材料.事实上布里渊区折叠效应也可以视为降低晶体对称性的重要效果之一.当然，直接带隙的物理来源还有其他因素，如导带底与价带顶波函数的对称性.作为晶体几何特征的结构对称性，通过晶体势或电荷密度分布而在电子结构性质上反映为带隙类型的转变是可以理解的.

2.4. 准粒子近似

根据格林函数理论建立起来的准粒子计算是通过求解方程(1)得到准粒子能量和准粒子波函数［16］，

方程(2)在该近似方法中不包括顶点修正［17］.

在GWA中，假设准粒子生存时间为无限长，且LDA的波函数与准粒子的波函数重合［12，18］(经过计算，准粒子的波函数与LDA的波函数重合率超过99%，因此这样假设是合理的).则单粒子格林函数可以写成

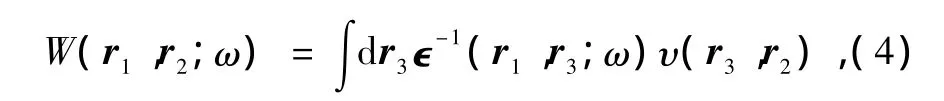
其中VLDAxc为LDA交换关联势.LDA本征能量中的交换关联作用部分用能量相关的自能算符贡献替代.这种近似方法得到的结果非常理想.

3. Si基材料模型

前面阐述的降低对称性原理为我们提供了计算设计的方向，使人们在执行能带结构计算之前确定晶体结构模型有章可循.对于Si基材料而言，可用两个基本方法降低晶体的对称性.

方法Ⅰ:在Si中进行原子替换或制作合金，使其对称性从Oh点群降为闪锌Td或体心四角(BCT)或对称性更低的结构.

方法Ⅱ:在Si中进行非Si原子的周期性原子插层，形成低对称性的材料.

在本文中，我们采用方法Ⅰ在Si(100)面上设计新的Si基超晶格Si1－xSnx/Si(100).由于我们选择方法Ⅰ设计新Si基超晶格，所以必须选择Ⅳ族元素作为Si的替代材料，否则不能保证新材料结构的稳定性.Ⅳ族元素有C，Si，Ge，Sn和Pb，根据芯态效应，我们应该选择芯态比Si大的元素，即Ge，Sn或Pb.显然Sn和Pb的芯态比Ge大.根据电负性差效应，选择Ge与Si的电负性最小，Sn次之，Pb与Si的电负性最大.至于对称性，无论选择Ge，Sn还是Pb作为Si的替代材料，新Si基超晶格的对称性都会降低.同时，我们注意到Pb的原子半径比Si大很多，选用Pb将可能导致材料稳定性差.综合考虑，我们选择Sn作为替代元素.计算所用的超晶格原胞见图1.

图1 SixSn1－x/Si的超晶格原胞(a)Si0.875Sn0.125/Si，(b)Si0.75Sn0.25/Si，(c)Si0.5Sn0.5/Si

4. 结果与讨论

在LDA计算中，我们选择平面波赝势法.模守恒赝势由Troullier-Martins(TM)方法构造得到［19］，采用Ceperley-Alder(CA)交换关联势［20］.布里渊区中k点通过6×6×3的Monkhorst-Pack方式［21］分割得到.截断动能为45 Ry(1 Ry=13.606 eV)，使总能收敛到0.001 eV.经过弛豫得到的Si1－xSnx/Si超晶格的晶格常数见表1.由于设计的超晶格材料还没有实验数据，所以在GWA计算中，我们采用LDA弛豫后的晶格常数.极化函数用平面波展开的截断动能为15 Ry，使自能收敛于0.05 eV.

表1 Si及Si1－xSnx/Si的晶格常数和带隙值

LDA计算得到的Si1－xSnx/Si超晶格能带图见图2.为了比较，我们计算了16个Si原子组成的简单四角结构超原胞.可以观察到，Si是间接带隙材料，价带顶在Γ处，导带底在Γ-X和Γ-Z方向. Si0.875Sn0.125/Si是直接带隙材料，带隙最小值点在Γ处.而Si0.75Sn0.25/Si和Si0.5Sn0.5/Si为间接带隙材料，价带顶在Γ点，导带底在Z点.由原胞的结构可知，Si0.875Sn0.125/Si的对称性比Si0.75Sn0.25/Si和Si0.5Sn0.5/Si要低.根据对称性效应，Si0.875Sn0.125/Si比Si0.75Sn0.25/Si和Si0.5Sn0.5/Si更有可能成为直接带隙材料.反过来，我们计算的例子也证明晶体材料对称性效应的正确性，即随着材料对称性的降低，其成为直接带隙材料的可能性增加.从图2可以看到，三种超晶格价带顶都在Γ.与Si相比，超晶格Z到Γ的导带底很平.这是因为我们所取的原胞中包含的原子数目增加，导致布里渊区发生折叠引起的.

在Si(100)面上构造的超晶格原胞是简单四角结构，在这个结构中，除了替代的Sn原子外，其他Si原子均在其正常位置附近.构造原胞时，在Si(100)表面上有序排列Si和Sn单层，然后加上七层Si，重复上述步骤得到Si0.875Sn0.125/Si.对应的布里渊区发生折叠，将Si(金刚石结构)中X点折叠到Γ点.我们知道，Si的导带底在X点附近，因为没有将导带底直接折叠到Γ点，所以Si0.75Sn0.25/Si和Si0.5Sn0.5/Si是间接带隙材料.但Si0.875Sn0.125/Si是直接带隙，这可能是由于Sn替代了Si原子，结构发生变化导致超晶格势扰动，从而分裂了折叠的能带和简并态.这种分裂会降低导带底的能量.

图2 LDA能带图(a)Si，(b)Si0.875Sn0.125/Si，(c)Si0.75Sn0.25/Si，(d)Si0.5Sn0.5/Si

Si和SiSn/Si超晶格的价带顶都在Γ点，而导带底在Γ-Z方向上.所以四种材料在Γ-Z方向导带底部的情况决定材料的性质.由于Si在Γ点导带底有多个能级简并，所以我们考察Γ和Z点的底部导带能级.

SiSn/Si超晶格中，Sn的芯态效应使导带底整体下移，随着Sn原子数目增加能带整体下移加剧.与Si导带底比较，Si0.875Sn0.125/Si，Si0.75Sn0.25/Si和Si0.5Sn0.5/Si在Γ点分别下移0.24，0.31和0.53 eV;在Z点分别下移0.10，0.30和0.48 eV.可以看到在Γ点下移的幅度比Z点大，这是因为Sn原子的加入，SiSn/Si超晶格的晶格常数发生变化.而Γ点的能量对晶格常数的变化比较敏感.

从图2可以看到，Si不论是价带还是导带都存在大量的简并态.Si中部分原子被Sn替换后，部分简并态分裂.随着Sn原子的加入，Γ点上Si导带底的六度简并能级分裂成五个能级.分裂后，这五个能级宽度为0.24，0.42和0.48 eV，分别对应Si0.875Sn0.125/Si，Si0.75Sn0.25/Si和Si0.5Sn0.5/Si.在Z点导带底部的六个能级宽度分别为1.22，1.43和1.59 eV，而Si对应的带宽为1.39 eV.

Si0.875Sn0.125/Si在Γ点能级下移的幅度和分裂的程度都比Z点大，而且与Si比较，Z点的底部导带能级宽度缩小，最终导致Si0.875Sn0.125/Si成为直接带隙材料.而Si0.75Sn0.25/Si和Si0.5Sn0.5/Si虽然在Γ点下移的幅度比Z点大(0.01和0.05 eV)，Γ点的能带分裂也比Z点明显，但是Si中Z点导带底比Γ点低0.08 eV.最终Si0.75Sn0.25/Si和Si0.5Sn0.5/Si Γ点导带底与Z点导带底很接近，但是导带的最小值在Z点.

SiSn/Si超晶格最小带隙值见表1.众所周知，LDA计算得到的带隙值与实验值之间存在很大的误差.大量研究表明，对于sp系统的半导体材料，GWA方法计算得到的带隙值与实验值之间的误差在0.1 eV内.由于直接带隙半导体材料Si0.875Sn0.125/Si有光电器件方面的潜在应用，所以准确预测直接带隙超晶格Si0.875Sn0.125/Si的带隙值对进一步研究该材料有重要的意义.

图3为Si0.875Sn0.125/Si的准粒子能带图.与Si0.875Sn0.125/Si的LDA能带图(见图2(b))相比，准粒子能带色散关系与LDA的整体相似.准粒子的计算结果表明，Si0.875Sn0.125/Si是直接带隙半导体，最小带隙值在Γ点.但是，其带隙值明显变大，ELgDA=0.35 eV，Eqgp=0.96 eV.这种变化是由于GWA中用自能算符Σ取代了LDA中的交换关联势VLxcDA引起的.

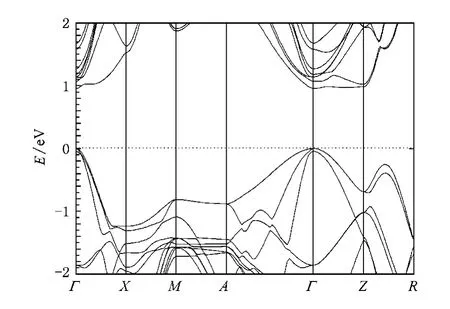
图3 Si0.875Sn0.125/Si的准粒子能带图

5. 结论

综上所述，我们利用原子芯态效应、电负性差效应和对称性效应，设计了SiSn/Si超晶格材料.由Si材料的结构和对称性效应设计了SiSn/Si超晶格材料的基本几何结构，然后通过原子芯态效应和电负性差效应选择适当的元素替代Si，本文我们选择Sn.在Si的(001)面上用Sn替代部分Si原子，得到一个四角结构的原胞.第一性原理和准粒子计算发现，Si0.875Sn0.125/Si是直接带隙超晶格，其最小带隙在Γ点.LDA的带隙值为0.35 eV，准粒子带隙值为0.96 eV，这为Si基材料生长实验提供了方向和理论依据.

［1］Gnutzmanu U，Clavsecker K 1974 Appl.Phys.3 9

［3］Canham L T 1990 Appl.Phys.Lett.57 1045

［4］Cullis A G，Canham L T 1991 Nature 353 335

［5］Hirschman K D，Tsybeskov L，Duttagupta S P，Fauchet P M 1996 Nature 384 338

［6］Walson W L，Szajowski P F，Brus L E 1993 Science 263 1242

［7］Pavesi L，Dal Negro L，Mazzoleni C，Franzo G，Priolo F 2000 Nature 408 440

［8］Huang M C，Zhang J L，Li H P，Zhu Z Z 2002 Chin.J. Lumin.23 419(in Chinese)［黄美纯、张建立、李惠萍、朱梓忠2002发光学报23 419］

［9］Huang MC2003TheoreticalPhysicsandaNumberof Interdisciplinary Frontier Major Research Projects and Academic Exchanges Collection Beijing，China，January 15—17，2003 pp197—208(in Chinese)［黄美纯2003“理论物理学及其交叉科学若干前沿问题”重大研究计划2002年度学术交流会，北京2003年1月15日—17日，第197—208页］

［10］Huang M C，Zhang J L，Li H P，Zhu Z Z 2002 Int.J.Mod. Phys.B 16 4279

［11］Hedin L 1965 Phys.Rev.A 139 796

［12］Hybertsen M S，Louie S G 1986 Phys.Rev.B 34 5390

［13］Shishkin M，Kresse G 2007 Phys.Rev.B 75 235102

［14］Fleszar A，Hanke W 2005 Phys.Rev.B 71 045207

［15］Huang M C 2005 Journal of Xiamen University(Natural Science) 44 874(in Chinese)［黄美纯2005厦门大学学报(自然科学版)44 874］

［16］Hedin L，Lundqvist S 1969 Solid State Physics(Vol.23)(New York:Academic)

［17］Sole R D，Reining L，Godby R W 1994 Phys.Rev.B 49 8024

［18］Hybertsen M S，Louie S G 1985 Phys.Rev.Lett.55 1418

［19］Troullier N，Martins J L 1993 Phys.Rev.B 43 1993

［20］Ceperley D M，Alder B J 1980 Phys.Rev.Lett.45 566

［21］Monkhorst H J，Pack J D 1976 Phys.Rev.B 13 5188

PACC:6185，7115H

†E-mail:mailoliver@126.com

Band structure of Si-based superlattices Si1－xSnx/Si

Lü Tie-Yu†Chen Jie Huang Mei-Chun
(Department of Physics，Xiamen University，Xiamen361005，China)
(Received 23 October 2009)

The prospects of Si-based optical emitting materials are optimistic because the materials are compatible with silicon microelectronics technology.Therefore，many experimental and theoretical studies are directed to the design of direct band-gap Si-based materials.Based on the core state effect，the electronegativity differences effect of component atoms and the symmetry effect，Si-based superlattices Si1－xSnx/Si were designed.We found that Si0.875Sn0.125/Si is a direct bandgap material.In the density functional theory frame，the results of plane pesupotential method show that Si0.875Sn0.125/Si is a direct band-gap superlattice with minimum band-gap at Γ point.We predict that the band gap of the material is 0.96 eV with the help of GW approximation method.

density functional theory，GW appoximation，Si-based superlattice

book=338,ebook=338

†E-mail:mailoliver@126.com