固支半球壳的随机响应分析
李军,冷小磊
固支半球壳的随机响应分析
李军*,冷小磊
(南京航空航天大学 振动工程研究所 飞行器结构力学与控制教育部重点实验室,南京210016)
在经典薄壳理论的基础上,采用数值计算分析了周边固支半球壳的固有模态。算出了轴对称自由振动固有频率和用勒让德函数表示的固有振型。在模态叠加法基础上,给出了横向激励下系统的响应特性。最后结合随机分析理论算出了壳体在横向白噪声激励下的均方响应,并给出了壳体各点的稳态均方响应曲线和时变均方响应曲线。
球壳;随机振动;均方响应
1 引言
壳体结构具有很好的空间传力性能,广泛应用于工程结构中。壳体结构在实际使用中,经常受到各种载荷的激励,而这些激励多是随机的。因此,有必要研究壳体结构在随机激励下的随机响应。而近一个世纪来,球壳振动问题,除了固有模态求解[1,2,7,13],对于强迫振动,大多数限于研究确定性振动响应问题[3,5,6]。由于20世纪50年代人们才开始随机振动的探讨,因此有关随机激励下的半球壳的响应,目前可见的文献中,还难以看到相关的研究成果。
对于连续系统的振动响应问题,通常的做法是先求出固有模态,并根据精度要求进行模态截断,即将连续系统的响应转化为前几阶模态响应的线性组合来研究。本文仍然采用上述传统做法,采用文献[1]的思想,借鉴了文献[13]中的处理方法,算出了周边固支半球壳的固有模态。然后结合模态叠加法[8]和随机分析理论[10],求出了壳体在横向分布激励下的响应特性,进一步算出了稳态白噪声激励下壳体的均方响应和突加白噪声情况下壳体各点的时变均方响应。
2 半球壳固有模态的求解
考察周边固支的半球壳,如图1所示,其中φ、θ分别表示壳体任一点的经向角、纬向角,u、v、w分别表示该点处的经向位移、纬向位移和横向(法向)位移。按照经典的勒夫薄壳理论,考虑壳
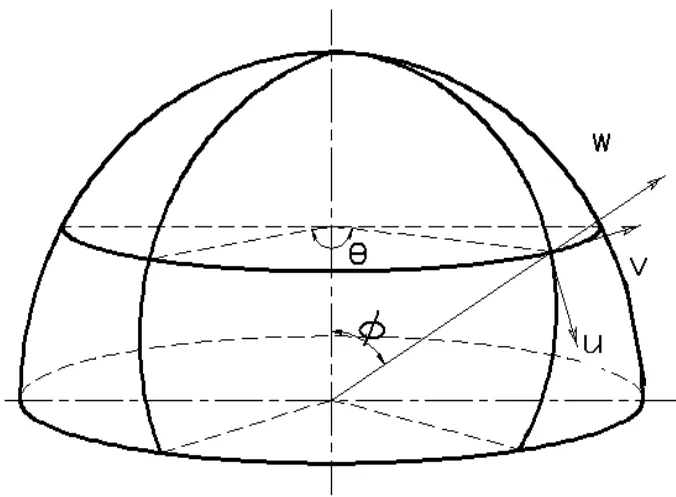
图1 半球壳示意图
体的薄膜刚度和弯曲刚度时,壳体的振动微分方程可以用下面的方程(1)、(2)来表示:[8]

对于轴对称情形,消去应力函数 f,结合分离变量法可得到关于横向振型函数W的方程[9]。
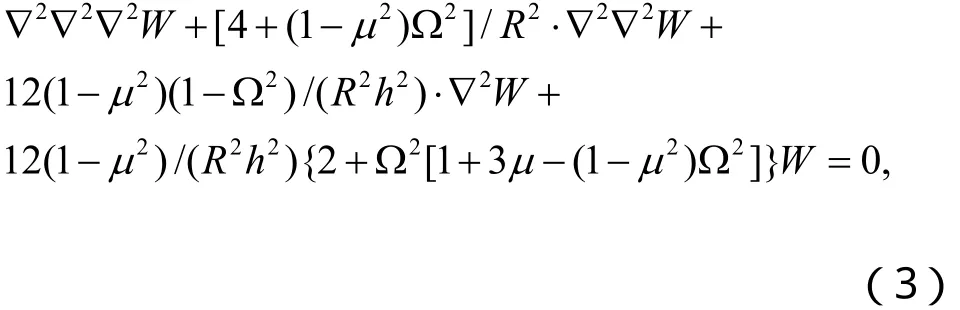
3 横向稳态随机白噪声激励下的壳体均方响应求解
求出系统的固有模态后,根据模态叠加法,壳体的响应可写为:

式中,ui(i=1,2,3)是位移响应在经向(u)、纬向(v)和横向(w)三个主方向的上的分量,Uik是第 k阶固有振型在三个主方向的上的分量,模态坐标ηk(t)是未知的待定函数。模态坐标 ηk(t)的方程可以写为(具体推导可以参见文献[8]):
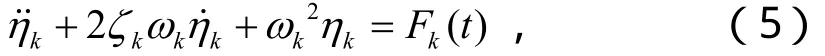
式中:

ζk称为模态阻尼系数,q1、q2、q3表示激励在三个主方向上的分量。由于本文只考虑轴对称情况,U2k和q2为零,U1k和U3k只和φ有关。在不引起混淆的情况下,下文中纵向位移U1k用Uk表示,横向位移U3k用Wk表示。
考察壳体只受横向均匀分布激励的情况下,方程(5)可以写为:
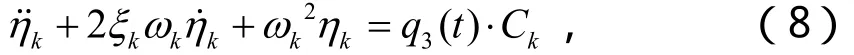
由方程(8),可以求出模态坐标 ηk(t)对横向均匀分布激励的频响函数。再结合方程(4)可以直接求出系统在横向激励下的频响函数H(φ, ω):

对于平稳随机激励,如果已知壳体各点受到的激励的功率谱密度,就可以根据随机振动理论求出系统位移的均方响应【10】。

这样,知道了随机激励的功率谱密度,通过上述公式可以很方便地求出壳体任一点处的位移均方响应。由于本模型的支撑条件为轴对称(周边固支),载荷也为轴对称(横向均匀分布激励),所以响应也必为轴对称,即半球壳的响应可以用任意一条经线上的响应来表示。在均匀分布横向白噪声激励的功率谱密度为 S(ω) = 106kg2/m2/s3时,壳体位移均方响应随φ的变化如图2所示。

(图2)
从图2中可以看出,在稳态白噪声激励下,壳体中心对称点的均方响应远大于壳体其他各点。而除了中心对称点,在纬向角大约0.4弧度和1.1弧度所对应的圆上,各点的均方响应也比邻近的点的均方响应要大。
4 横向突加白噪声随机激励下壳体的时变均方响应
上面求出了壳体上各点在随机平稳白噪声横向激励下的稳态位移均方响应,对于壳体在突加白噪声激励下的时变位移均方响应,本文按虚拟激励法进行求解。假设方程(5)中,各模态响应的初始条件为 ηk(0) =η˙k(0)= 0。q3( t)表示突加横向白噪声,q3( t) = g( t) · x( t),x( t)表示零均值的随机白噪声,功率谱密度 S0= 106kg2/m2/s3为已知,g( t)为单位阶跃函数。
采用虚拟激励法[11],求出方程(5)的解为:

此时,模态坐标ηk( ω, t)的时变功率谱密度为:
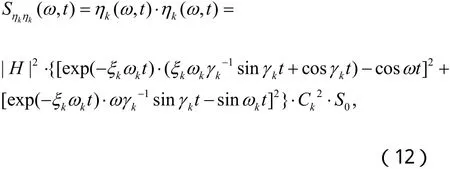
其中,等号右边的上横线表示取复数 ηk( ω, t)的共轭。
对上式在频域上积分可得模态坐标 ηk(t)的时变方差为[11]:

其中,

由方程(6),在只考虑轴对称情况下(轴对称时,不考虑环向坐标θ),可以推出:

因此,如果知道了模态坐标的时变方差,结合振型函数,利用公式(14),可以求出球壳任一点的均方响应随时间的变化情况。球壳极点处在突加横向均匀分布白噪声激励下均方响应的瞬态过程如图3所示。

(图3)
5 总结
本文借助经典薄壳理论,结合随机响应问题的虚拟激励方法,分析计算了横向均匀分布的白噪声激励下周边固支半球壳的均方响应。稳态响应的计算结果表明,壳体极点(中心对称点)的均方响应为最大(见图2);而突加载荷作用时壳体极点处位移均方响应的时变方差曲线表明,由于系统中结构阻尼的存在,使得均方响应随着时间的推移逐渐从下方趋向于稳态值。上述结果符合客观实际,也佐证了本文所述方法适用于轴对称情形下壳体的随机响应分析。然而,如何将这类方法推广到非轴对称情形,尚有待进一步的研究。
[1] Kalnins A. Effect of bending on vibrations of spherical shells [J]. J Appl Mech, 1963, 36: 74-81.
[2] Kalnins A. Free vibration of rotationally symmetric shells [J]. The Journal of the Acoustical of America, 1964, 3(7): 1355-1365.
[3] Anand V Singh. Transient response of thin elastic spherical shells [J]. J Acoust Soc Am,1980, 68(1): 191-197.
[4] Singh A V. General vibration theory of deep spherical sandwich shells [D]. Canada: University of Ottawa, 1975.
[5] Kraus H, Kalnins A. Transient Vibration of Thin Elastic Shells [J]. J Acoust Soc Am, 1965, 38: 994-1002.
[6] Naghdi P M, Kalnins A. On vibrations of elastic spherical shells [J]. J Appl Mech, 1962, 29: 65-72.
[7] Kalnins A. Analysis of shells of revolution subjected to symmetric and nonsymmetric loads [J]. J Appl Mech, 1964, 31: 467-476.
[8] Werner Soedel. Vibrations of shells and plates [M]. New York: Marcel Dekker. 1981:199-226.
[9] 曹志远. 振动理论[M]. 北京:中国铁道出版社, 1989:327-343.
[10] 方同. 工程随机振动[M]. 北京:国防工业出版社, 1995:69-116.
[11] 林家浩. 张亚辉. 随机振动的虚拟激励法[M]. 北京. 科学出版社, 2004:60-65.
[12] 孙庆鸿,张启军,姚慧珠. 振动与噪声的阻尼控制[M]. 北京. 机械工业出版社, 1993:74-77.
[13] 尚新春. 密封容器组合壳自由振动的精确解[J]. 应用数学和力学,2001, 22(9):934-942.
[14] 马晓兵,尚新春,韩明芬. 柱壳和球壳振动的固有频率计算及模态分析[J]. 工程力学,2002(增刊):332-335.
[15] 黄克智,夏之熙,薛明德,等. 板壳理论[M].北京,清华大学出版社,1987:133-172.
[16] 纽兰 D E. 随机振动与谱分析概论[M]. 方同,黄嘉璜,朱位秋,译.北京:机械工业出版社,1980:55-70.
[17] 胡海岩,孙久厚,陈怀海. 机械振动与冲击(修订版)[M]. 北京:航空工业出版社,1998:47-56.
Random Response Analysis of Semi-spherical Shell with Clamped Edge
LI Jun,LENG Xiao-lei
(Institute of Vibration Engineering Research, MOE Key Lab of Structural Mechanics and Control for Aircraft, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
Based on classical thin shell theory, intrinsic mode of a semi-spherical shell with clamped edge is analyzed by means of numerical calculation. Natural frequencies of free vibration under circumstances of axi-symmetry modes and natural modes of viberation expressed in terms of the Legendre functions are also calculated. Furthermore, based on the mode superposition method, response characteristics of horizontal excitation are presented. Finally, the mean square response of the shell excited by horizontal white noise is calculated in combination with the stochastic analysis theory, with transient/variable mean square response curves at each point of the shell presented.
spherical shell; stochastic vibration; mean square response
O383
A
1009-5160(2010)01-0035-04
*通讯作者:李军(1970-),男,硕士,研究方向:板壳随机振动研究.基金项目:国家自然科学基金资助项目(10672074).

