基于第二代小波的增强边缘的图像去噪
林祥云,马俊,赵慧娟
基于第二代小波的增强边缘的图像去噪
林祥云,马俊*,赵慧娟
(武汉科技学院 理学院,湖北 武汉 430073)
传统的一些去噪技术往往是以牺牲图像的边缘和细节为代价的。为了去掉图像的噪声,同时又能够很好地保留图像的边缘和纹理细节,在介绍第二代小波变换的原理的基础上,提出使用边缘检测的方法检测出图像的边缘和纹理细节,将它和该图像进行融合,用第二代小波对含噪图像进行分解, 对图像高频进行自适应去噪。由于图像在去噪前融合了边缘信息,因此边缘和细节部分得到了增强。仿真结果表明:该去噪方法优于传统小波阈值去噪方法。
第二代小波变换;边缘增强;图像去噪
1 引言
随着小波理论的日益完善,它以自身良好的时频特性在图像降噪领域受到越来越多的关注,但在实际应用过程中,传统小波变换存在计算量大、存储空间消耗大以及浮点计算的缺点[1]。为此,1994年Sweldens提出了一种不依赖于傅立叶变换的新的小波构造方法——提升方法,基于提升方法的小波变换称为第二代小波变换(Second Generation Wavelet)[2,3]。提升方法可以不依赖傅立叶变换而直接在空域完成计算、原位计算(不需要额外存储空间) 、易实现整数到整数的变换以及计算量更小的特点[4],成为小波研究与应用领域的新热点。
传统的小波去噪方法虽然将去噪的技术引入到频域,并且在去噪的过程中一定程度上保留了大的高频系数,但是那些偏小的边缘和纹理的小波系数还是被缩减甚至去掉了,因此无法很好地保持边缘和细节。
本文利用第二代小波变换特性,寻求一种既能够去掉图像的噪声,同时又能够保留图像的边缘和纹理细节的方法。为了达到这个目的,考虑到在去噪之前首先用边缘检测的方法检测出含噪图像的边缘和纹理细节,将它和含噪图像以一定的比例进行融合,再用第二代小波变换对融合后的图像进行分解, 对图像高频进行自适应去噪处理,最后将阈值化后的小波系数重构,得到去噪后的图像。
2 第二代小波变换原理
提升方法给出了双正交小波简单而有效的构造方法,使用了基本的多项式插补来获取信号的高频分量,之后通过构建尺度函数来获取信号的低频分量。提升方法的基本思想是,将现有的小波滤波器分解成基本的构造模块,分步骤完成小波变换。1998年, Daubechies 和Sweldens 证明了任何离散小波都可以用提升方案[5]来实现,提升方法把小波变换过程分为以下3 个阶段[6,7]。
①分裂。将输入信号sj, 分裂成为两个互不相交的子集sj−1和dj−1,常用的算法是将输入信号按奇偶分成两个子集,
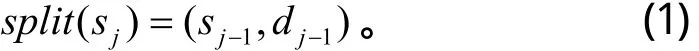
②预测。针对数据间的相关性,可用sj−1的预测值 p( sj−1)去预测奇数序列dj−1,即将滤波器p对偶信号作用以后作为奇信号的预测值,奇信号的的实际值与预测值相减得到残差信号。若用子集dj−1与预测值 p( sj−1)的差值去代替dj−1,则此差值反映了两者的逼近程度。如果预测是合理的,则差值数据集所包含的信息比原始子集dj−1包含的信息要少得多。预测过程的表达式:
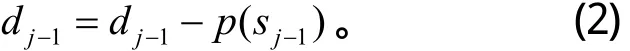
③更新。由于分解成子集,原来集合的一些特征丢失,通过更新使子集的数据和原来集合的数据保持相同的特征。也就是通过算子U 产生一个更好的子数据集sj−1,使之保持原数据集sj,的一些特性。sj−1的表达式:
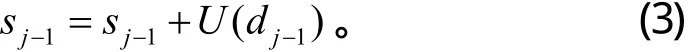
小波提升是一个完全可逆的过程,重构数据时的提升公式与分解公式相同,改变计算次序和符号就可以了。
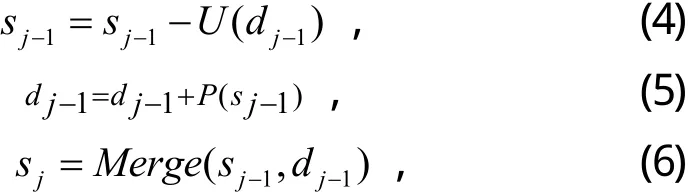
其中Merge是合并的意思,是将分裂后的子集sj−1和 dj−1重构成初始信号sj。
3 基于第二代小波的图像去噪
3.1 去噪模型建立
假设T( i, j)为含噪的图像,可以表示成一个M× N的矩阵:
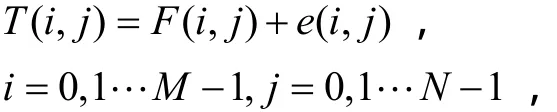
式中F( i, j)原图像,e( i, j)为平稳的零均值白噪声。
3.2 增强边缘信息
去噪和边缘细节的保留是图像去噪存在的两个问题。去噪的目的是消除噪声尤其是那些存在于高频的噪声,但是图像的细节也处于信号的高频部分。传统的去噪技术如wiener 滤波等时域滤波的去噪都是以牺牲图像的边缘和细节为代价的[8],为了在去噪的同时较好的保留图像边缘信息,本文在去噪前对图像做了边缘增强工作。
函数的导数反映图像灰度变化的显著程度,一阶导数的局部极大值和二阶导数的过零点都是图像灰度变化极大地方。因此可将这些导数值作为相应点的边界强度,通过设置门限的方法,提取边缘。
Soberts算子是一种利用局部差分算子寻找边缘的算子,它对灰度渐变和噪声较多的图像处理较好[13]。
利用soberts边缘检测算子,检测出含噪图像的边缘G( i, j),并对G( i, j)和含噪图像T( i, j)作小波变换,得到它们的小波变换系数 Wg( i, j)和 Wt( i, j),然后将 Wg( i, j)和 Wt( i, j)进行融合,为了避免边缘的过分增强,加入调整系数k,
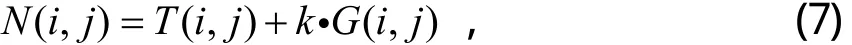
其中N(i,j)为融合后的小波系数,由N( i, j)重构得到增强边缘的含噪图像N*(i, j),利用第二代小波变换对进行阈值去噪。
3.3 图像去噪
利用第二代小波对二维图像进行n层的分解,最终将有(3n+1)个不同频带,其中包含3n个高频带和一个低频。含噪图像经小波多尺度分解后,噪声能量主要分布在各阶高频子带中,且在低阶小波系数中,噪声能量占有较高的比重,并随着小波变换级数的增长而减小,所以在各阶高频子带中选用适当的阈值来滤除噪声[9]。
由于传统的软阈值去噪使用的是单一阈值对小波系数进行处理,因此各个不同尺度的小波系数使用的是同样的阈值,但是单一的阈值函数不能在每级尺度上将信号与噪声做很好的分离。所以,为了达到更好的去噪效果,针对不同的高频的小波系数本文用ddencmp函数计算相应的默认阈值[1], 用阈值化后的小波系数重构,得到去噪后的图像。
4 试验及仿真结果分析
对Matlab7.5系统中的woman和cameraman图像加入均值为零,标准差为18的高斯白噪声,选用sym4小波基函数,根据提升方法得到二代小波(提升sym4小波),用本文提出的方法和传统小波阈值去噪方法进行去噪实验。且采用峰值信噪比(PSNR)和均方误差(MSE)对去噪结果进行对比和分析[14-16]。
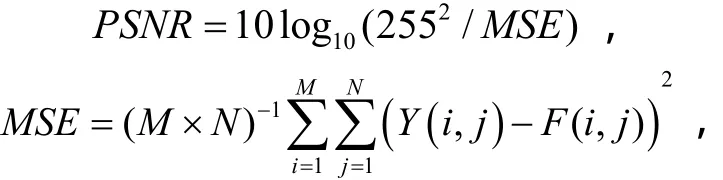
式中,M和N分别为对应图像的行数和列数; F( i, j)和Y( i, j)分别为原图像和去噪像。实验步骤如下:
①采用soberts算子,调用MATLAB系统中的edge()函数提取边缘G( i, j),如图1所示。
②选择sym4小波,由提升方法得到二代小波,对二维含噪图像T(i,j)和它的边缘G( i, j)进行小波分解,得到小波系 Wt( i, j) 和 Wg( i, j)。
③将小波系数 Wg( i, j) 和 Wt( i, j),按(7)式融合。然后重构得到边缘增强的含噪图像 N *(i, j)。
④对增强边缘的含噪图像 N *(i, j)进行2层小波分解,得到第一层和第二层的水平高频系数、垂直高频系数和对角高频系数,然后用ddencmp函数计算各个高频的默认阈值,并对各个高频阈值化处理。
⑤利用处理后的小波系数,进行反变换得到去噪后的图像,并对去噪结果进行数值评价。
从图2 来看, 本文提出的去噪方法使去噪后的图像纹理更清晰,图像主观效果更好。
采用本文方法去噪和传统小波阈值去噪所得的均方误差和峰值信噪比如表1所示,从表1中可以看出采用本文方法进行图像消噪所得的图像的均方差更小,峰值信噪比更大,也说明去噪效果更好。

图1 图像边缘
5 结束语
为了更好的保护图像的边缘和纹理,本文结合第二代小波变换的优越性在去噪前首先作了边缘增强工作。实验结果表明,本文方法不仅降低了均方误差,提高了图像的PSNR的性能,对图像噪声进行了较好的抑制,而且更好的保持了图像的边缘和纹理特性。
[1] 张德丰. MATLAB小波分析[M].北京:机械工业出版,2009:206-209.
[2] Wim Sweldens. The lifting scheme: a construction of second generation wavelets[J].SIAMJ MathAnal, 1997, 29(2): 511-546.
[3] Donoho D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory,1995 ,41(3): 613-627.
[4] Donoho D L, Johnstone I M. Ideal spatial adaptation viawavelet shrinkage[J]. Biomerika, 1994,81(4): 425-455.
[5] Daubexhies I, Sweldens W. Factoring wavelet transforms into lifting steps[J]. JFourierAna l, 1994, 4(3): 245-267.
[6] Sweldens W. The lifting scheme: A construction of second generation wavelets[J].SIAM Journal on Mathematical Anal ysis ,1997,29(2):511-546.
[7] 葛哲学,沙威.小波分析理论与MATLAB R2007实现[M].北京:电子工业出版社,2007:375-380.
[8] 胡昌华,张军波,夏军,等.基于 MATLAB 的系统分析与设计——小波分析[M].西安:西安电子科技大学出版社,1999:226-230.
[9] 李杏梅,陈亮,严国萍.基于自适应软阈值和边缘增强的图像去噪[J].电子测量技术,2008,31(7): 4-6.
[10] Donoho D L. De-noisingby soft-thresholding[J].IEEE Trans on Inform Theory, 1995,41(3): 613-627.
[11] CHANG S G, YU B , Vetterli M. Adaptive wavelet thre sholding for image denoising and compression [J]. IEEE Transactions on Image Processing,2000,9 (9): 1532-1546.
[12] 王爱玲,叶明生,邓秋香. MATLAB R2007图像处理技术与应用[M].北京:电子工业出版社,2008:116-169
[13] 董楠,蒋本和,徐福泽.基于第二代小波变换的图像除噪[J].烟台大学学报:自然科学与工程版, 2007,20(1): 4.
[14] 刘菁.小波分析在织物起毛起球客观评级中的应用[J].武汉科技学院, 2009, 22(4):7-10.
[15] Donoho D L,Johnstone I M. Wavelet shrinkage asympot[J].Pia journal of royal sattistical soeieyt,1995.57(2):301-369.
[16] 杨占英. 关于Meyer型小波的一个注记[J].武汉科技学院学报, 2009, 22(4): 32-34.
Image Denoising Using Enhanced Edge Information Method Based on Second Generation Wavelet
LIN Xiang-Yun, MA Jun, ZHAO Hui-Juan
(College of Science, Wuhan University of Science and Engineering , Wuhan 430073, China)
The traditional denosing methods are often applied at the cost of sacrificing the edge and texture detail of the images. In order to denose and retain the edge and textile detail of the image, this paper proposes a method of enhanced edge information based on the principle of second generation wavelet. First, use the edge detection method to detect the edge and texture detail of the image. Second, fuse the image and its edge and texture detail in order to enhance the parts of edge and texture detail. And then, decompose the fused image by second generation wavelet. Last, make the adaptive threshold denoising for the high frequency of the fused image. The simulation shows that the edge and texture detail of fused image has been enhanced. Comparing to the traditional wavelet threshold denosing method, the method proposed in this paper is much better in improving the visual effects and signal-to-noise.
second generation wavelet transform; edge enhancement; image denoising
TP391
A
1009-5160(2010)01-0028-04
*通讯作者:马俊(1963-),男,教授,研究方向:小波分析的理论及应用.基金项目:武汉科技学院院基金(20073201).

