科技英语中时空语言的解读

王 蕾

（西南交通大学外国语学院，四川成都 610031）

科技英语中时空语言的解读

王 蕾

（西南交通大学外国语学院，四川成都 610031）

本文着重对科技英语中的时间语言、空间语言及时空关联语言的中英文进行解读。

时空关联语言；速度；加速度；牛顿力学；频率；微粒的波粒二象性

1.前言

科学技术是人类的公共资源，各国人民都可交流使用。“科学技术是第一生产力（邓小平1993：377-378），推动着生产力向前发展，引起了社会的巨大变革。作为外国语言教学，不仅要学习传承人文、社会科学语言，也要学习传承科学技术语言，使中西文化、科技相互交融，取长补短，让科学技术语言成为人们的社会生活语言。

1.1 时空语言（language of time and space）

时间语言 （time language）是由基本词汇如某时刻、某段时间、某方向时间间隔等与其相关词汇构成的短语和句子。

空间语言（space language）是由基本词汇如某点、某段距离、某方向位移、面积、体积、波长等与其相关词汇构成的短语和句子。

时空关联语言是由描述物体运动的空间位移和时间间隔的基本语言，以及具有时间（time）和空间（space）特性的词汇相互关联而构成的词汇、短语和句子。如速度、加速度、光速度、频率等。

1.2 物体—运动—时空具有紧密关联的三角关系

单独的时间与空间概念太抽象，不知所云，如与物体和运动关联，三者相互依存，不弃不离构成紧密关联的物体—运动—时空三角关系：世上没有不运动的物体，也没有脱离物体的运动，只有时间和空间能表述物体运动的存在形式。如“朝辞白帝彩云间，千里江陵一日还”，诗人（物体）早上（某时刻）从白帝城（某地为始点）出发，经过一天的时间，船行千里（空间）到达江陵 （某地为终点）。又如，“坐地日行八万里”，坐在地上的人，靠地球自转，一天的时间，也相当于走了八万里。这些例子都说明，物体始终处于运动状态，运动着的物体必须用时间语言和空间语言描述其运动行为，同时也指出了物体运动的方向（矢量）特性。

但是，人文学科的时空语言中，少有时间与空间发生关联的语言，如移动的路程（空间量）除以时间得到速度、微粒振动次数（空间量）除以时间得到频率等时空关联构成一体的概念。时空关联语言在科技语言中应用特别广泛。

1.3 两种世界两种运动学

①宏观世界（macrocosm）：宏观物体作宏观运动，是低速运动，位置移动，机械运动等等，产生了研究物体间作用力规律的牛顿力学（Newtonian mechanics）。

② 微观世界（microcosm）：微观粒子作微观运动，是高速运动，用光和实物粒子的波粒二象性表述其运动行为，并产生了研究微观粒子属性和规律的量子力学（quantum-mechanics）。

2.用时空语言表述宏观物体的运动力学

2.1 用时空语言表述物体的运动速度

宏观物体的运动如火车、汽车、轮船、飞机、飞禽和走兽等。物体的运动速度用时间量（数与时间单位的乘积，如3秒写成3s）和空间量（数与长度单位的乘积，如5米写成5m）相关联的变化来表述。一般把宏观物体视为质点（质量为零的几何点）描述其运动行为较方便。

2.1.1 质点的平均速度 （average velocity of the particle）

质点的平均速度用符号v表示，质点在空间运动的距离（displacement）为△x，其运动的时间间隔（time interval）为△t。质点的平均速度等于质点的运动距离除以（数学符号用‘÷’或‘/’）质点运动的时间间隔，用数学式表示为：

由式⑴可以看出距离用长度米 （m），时间用秒（s）为单位，用国际单位制（SI units）表示质点平均速度的单位是m/s，读成米每秒。再明确强调一下，物体运动的平均速度是表示单位时间内物体运动的距离，可以是多少千米每小时（习惯说成每小时多少公里）、多少米每秒（习惯说成每秒多少米）。△x是运动距离的改变量△x=xf－xi，是由终点位置量xf减去始点位置量xi；△t是时间间隔的改变量△t=tf－ti， 是由终点时刻量tf减去始点时刻量ti。

质点的平均速度用英语语言表述（Sterway 1983:27）：

From this definition,we see that average velocity has the dimensions of length divided by time or m/s in SI units.

2.1.2 质点的瞬时速度 （instantaneous velocity of the particle）

质点的瞬时速度有时又称即时速度，用符号v表示，表示质点在某瞬时间（△t→0，即时间间隔趋于零但不为零，还可以理解为‘某时刻’附近）运动的距离（displacement）为△x，其运动的瞬时时间间隔（time interval）为△t。质点瞬时速度v等于质点的运动距离除以（数学符号用‘÷’或‘/’）质点运动的某瞬时间的平均速度取极限值（limiting value），用数学式表示为：

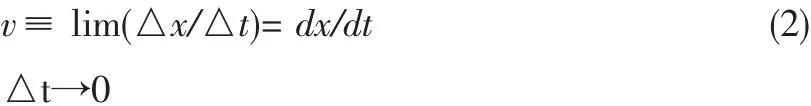
式(2)可以理解为把时间间隔分成无限小量，用dt表示，相对应的是运动距离也同样分成无限小量，用dx表示。瞬时速度v可以表示为dx/dt，即v=dx/dt。

v=dx/dt在数学领域称微商或导数，可以说成是x对t的微分，并有专门的运算方法。由此发现瞬时速度有正值（表示瞬时速度在增加）、负值（表示瞬时速度在减小）或零（表示瞬时速度为零，即质点处于某点上）。

质点的瞬时速度用英语语言表述（Sterway 1983:28）：

The instantaneous velocity,v,equals the limiting value of the ratio △x/△t as△t approaches zero:v≡lim(△x/△t)

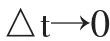
In the calculus notation, this limit is called the derivative of x with respect to t,written dx/dt:

The instantaneous velocity can be positive,negative,or zero.

2.1.3 质点的平均加速度 （average acceleration of the particle）

质点运动不仅有距离与时间的变化关系，还有运动速度与时间的变化关系。运动速度与时间的变化关系称为加速度，加速度有平均加速度和瞬时加速度。

质点平均加速度用符号a表示，质点平均加速度表示在某段时间间隔内 （△t=tf－ti）速度的改变量（△v=vf－vi）除以时间间隔（△t）。

式(3)中△v是空间运动速度的改变量vf－vi，是由终点速度量vf减去始点速度量vi。速度量的单位是米每秒（m/s），平均加速度的单位=平均速度的单位（m/s）除以时间（s），即 m/s/s=m/s2，读成米每秒每秒，写成 m/s2。

质点的平均加速度用英语语言表述（Sterway 1983:30）：

The average acceleration of the particle in the time interval△t=tf－tiis defined as the ratio △v/△t,△v=vfviis the change in velocity in this time interval:

Some of the common units of acceleration are meters per second per second(m/s2).

2.1.4 质点的瞬时加速度（instantaneous accelera-tion of the particle）

质点的瞬时加速度（a）又称即时加速度或加速度是质点运动在某瞬时间（△t→0，即时间间隔趋于零但不为零，还可以理解为‘某时刻’附近）的平均加速度（△v/△t）取极限值（limiting value）定义为瞬时加速度，表示式如下：

由于式(4)的v=dx/dt，加速度也可以写成：a=d(dx/dt)/dt=d2x/dt2,即加速度（a）等于相同坐标方向的空间距离x对时间t的二阶微分（d2x/dt2）。

质点的瞬时加速度用英语语言表述（Sterway 1983:31）：

The instantaneous acceleration as the limit of the average acceleration as△t approaches zero.

Since v=dx/dt,acceleration can also be written.

That is acceleration equals the second derivative of the coordinate with respect to time.

物体通过运动距离与时间的比（相除），引入了物体运动的平均速度v、瞬时速度v、平均加速度a和瞬时加速度a等时空统一一体的时空语言。为了引入“某时刻”，又提出了“时间间隔趋于零（△t→0）”的概念，由于时间间隔趋于零与之对应的平均速度和平均加速度就得到其极限值，这就引入了瞬时速度和瞬时加速度。这类描述物体运动的语言具有鲜明的物理特性和哲理性，对于理工科和社会学科的大学生都是非常需要和有益的。

从瞬时速度（v=dx/dt）和瞬时加速度（a=d2x/dt2）的表述式发现，研究物体运动状态从静态发展到动态，可以得到运动物体任一时刻的瞬时速度（v）和加速度（a）。

2.2 用时空语言表述宏观物体间的作用力

宏观物体间的作用力，用牛顿力学三定律表述：第一定律指出物体在外力作用下才能改变其运动状态；第二定律是表述力、质量和加速度之间的关系；第三定律是表述力具有物体间相互作用的性质。三个定律都涉及到力，物体间的作用力用时间量、空间量和质量（m）（数与质量单位千克的乘积，如3kg）等单位表述。

2.2.1 牛顿第一定律

又称惯性定律 （Newton’s first law and inertial frames）：简单的说，任何物体都具有保持运动状态不变的性质，这个性质叫惯性。一个物体没有外力作用下，它将保持其静止或匀速运动的状态不变。用数学形式表述为：F（外力）=0 时，v（匀速）=恒量。 表明了力是物体运动状态发生变化（即得到加速度）的原因。

2.2.2 牛顿第二定律（Newton’s second law）

实验中发现，当外力（可以是合外力∑F）作用到物体上时，力（F）与加速度（a）成正比（F∝a），质量（m）与加速度成反比（1/m∝a），其数学表达式：F×1/m∝a，设比例系数为K，则F=Kma，当力的单位选取牛顿（N），质量单位选千克（kg），加速度的单位选米每秒每秒（m/s2）时，K=1，即 1N=1kg·m/s2，读成“1 牛顿等于1千克·米每秒每秒”，故第二定律可以写成：

式(5)又因为加速度 a=dv/dt=d(dx/dt)/dt=d2x/dt2，第二定律还可以写成：

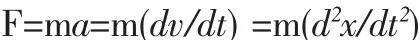
第二定律表明：当物体质量一定时，合外力(∑F)的作用下，物体作加速运动。说明外力是一个与时空关联的时空语言。

牛顿第二定律用英语语言表述（Sterway,1983:32）：

This is the most general form of Newton’s second law.

Since acceleration is defined as a=dv/dt=d/dt(dx/dt)=d2x/dt2,Eg.(5)can be written

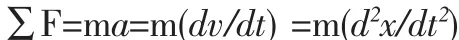
2.2.3 牛顿第三定律（Newton’s third law）

两个物体之间的作用力F和反作用力F′，在一直线上，大小相等，方向相反，分别作用在两个物体上。 可以表述为：F=－F′。

3.用时空语言表述微观粒子的运动特性

微观粒子分静止质量 （rest mass）为零的如光（量）子（light quantum 或 photon）和实物粒子（material particle 或 photon）如电子（electron），都是高速运动的粒子，都具有波动性和粒子性又称波粒二象性（wave-particle duality）。 波动性用时空语言波长（λ）和频率（f）表述；粒子性用涉及时空语言的能量（E=hf）和动量（p=h/λ）表述。波长指完成一个周期波的长度或完成一个完全振动的长度称波长。频率指单位时间内完全振动的次数。频率（f）、波长（λ）是时空关联的物理量。

3.1 光的波粒二象性

光已确定是电磁波，同时也是一束由光子组成的微粒流。用波长λ和振动频率f表述波动性；用光子能量（E=hf）和动量（p=h/λ）表述微粒性，二者又是通过普朗克常数 （h）把振动频率f和波长λ联系起来。由能量与动量公式发现，频率f越高能量越高；波长λ越短动（能）量越高。

光是微粒和波动的矛盾统一体，在不同的场合下，可侧重于一个方面的性质。在光的发射过程中，或在与实物相互作用时，光的微粒性表现较突出，如有关电磁波辐射（electromagnetic wave radiation)、光电效应（photoelectric effect）、黑体辐射（black body radiation）等现象就要用微粒说来解释；光在空间传播，如光的干涉（interference）和衍射（difference）等现象就得用波动说来解释。

光的波粒二象性用英语语言表述（Sterway 1983:872）：

We have presented very convincing evidence supporting the photon (particle)concept of light.On the one hand,we describe light in terms of photons with energyhfand momentumh/λ.On the other hand,we must also recognize the fact that light and other electromagnetic waves exhibit interference and difference phenomena.

We have given evidence which shows that all forms of electromagnetic wave radiation can be described from two points of view. In one extreme, electromagnetic wave describes the overall interference pattern formed by a large number of photons.In the other extreme,the photon description is natural when we are dealing with a highly energetic photon of very short wavelength.Hence,light has adualnature;it exhibits both wave and photon characteristics.

3.2 实物粒子如电子的运动特性

德布罗意受到光的波粒二象性的启发，假定由粒子构成的物质，其实必定伴随有波，从而带有波的性质。并且提出适合于光的两个著名关系，也同样适合于电子等实物粒子，即 E=hf，p=h/λ。

对于一个质量为m，而运动速度为v的实物粒子，其动量p=mv，由此得出德布罗意波长的关系式：

说明波粒二象性不仅适用于静止质量为零的光子，也适用于实物粒子。

用时空语言表述德布罗意实物粒子波长（Sterway 1983:873）：

De Broglie suggested thatmaterial particles of momentum p should also have wavelike properties and a corresponding wavelength. Since the momentum of a particle of mass m and velocityvisp=mv, thede Broglie wavelengthis

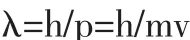
结束语

物质语言、时间语言和空间语言在物质运动的物理特性描述中应用较广泛。特别是时、空语言相关联形成的时空语言如瞬时速度、加速度、波长、频率等，大大推动了现代物理科学语言的发展。

Raymond A,Serway(1983).Physics[M].New York:CBS College Publishing.

邓小平(1993).邓小平文选第三卷[M].北京：人民出版社。

南京工学院等七校编(1981).物理学[M].北京：高等教育出版社。

潘道皑，赵成大，郑载兴等(1982).物质结构[M].北京：高等教育出版社。