三维复Ginzburg-Landau方程的一些精确解

罗森月，杨荣晖，钟澎洪

（1.广东广播电视大学工程技术系,广东广州510091；2.云南民族大学数学与计算科学学院,云南昆明650091；3.北京工业大学应用数理学院,北京100124）

三维复Ginzburg-Landau方程的一些精确解

罗森月1，杨荣晖2，钟澎洪3

（1.广东广播电视大学工程技术系,广东广州510091；2.云南民族大学数学与计算科学学院,云南昆明650091；3.北京工业大学应用数理学院,北京100124）

通过辅助函数法与齐次平衡原理,得到了三维复Ginzburg-Landau方程的一些精确周期波和扭结波解.

Ginzburg-Landau;辅助函数法;周期波;扭结

0 引言

复Ginzburg-Landau方程(CGLE）描述了定性或是定量的各类物理现象：从非线性波到二阶相变，从超导、超流体和玻色爱因斯坦凝聚到晶体场理论，甚至在弦理论中都能找到相关的物理背景.在物理学中，有大量关于CGLE这一非线性方程的研究.本文中，笔者研究如下CGLE：

其中：u是定义在n＋1维空间－时间Rn＋1上的复值函数；Δ是Rn上的拉普拉斯算子；ρ＞0,γ,μ是实参数.

在数学和物理的各学科分支中，对方程(1)都有广泛的研究.本文主要对方程(1)的精确解进行构造.在非线性科学中，(1)的解的适定性和孤立波特性已有很多结果.例如：变系数三维CGLE的亮孤立子和暗孤立子解的稳定性[1]；关于二维CGLE的同宿轨理论和精确孤立子解[2].在一些假定的特殊条件下，文献[3-4]求出了CGLE一些孤立子的解.最近，三维CGLE解的存在性和唯一性已被证明[5].本文中，笔者使用雅可比椭圆函数方法[6]和辅助函数法[7]及齐次平衡原则，得到一些三维CGLE新的精确解，其中包括周期波和扭结波解.

1 辅助函数法

考虑三维CGLE(1)：

将(2)代入方程(1)并消去eiωt，得到

将实部和虚部分离，得到

将(5)代入方程(3)和(4)，得到非线性常微分方程组

其中：A＝α12＋α22＋α32.

作辅助函数

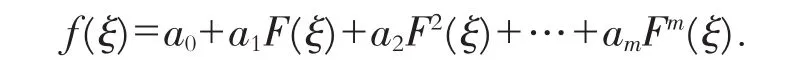
其中F(ξ)满足如下方程：

利用f″和f3关于F的最高阶相同（即齐次平衡原理），得m＋2＝3m，即m＝1，由此得到

其中：a0,a1是待定常数.

将(9)代入式(6)和(7)，得

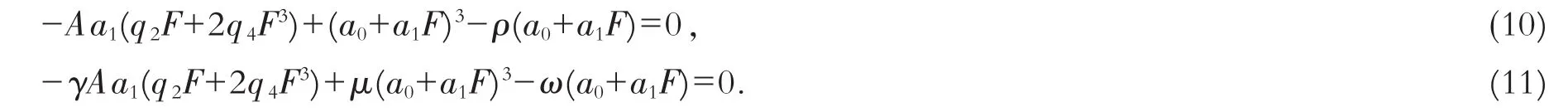
在（10）和（11）中让F的不同次幂的系数分别为0，得到如下代数方程：

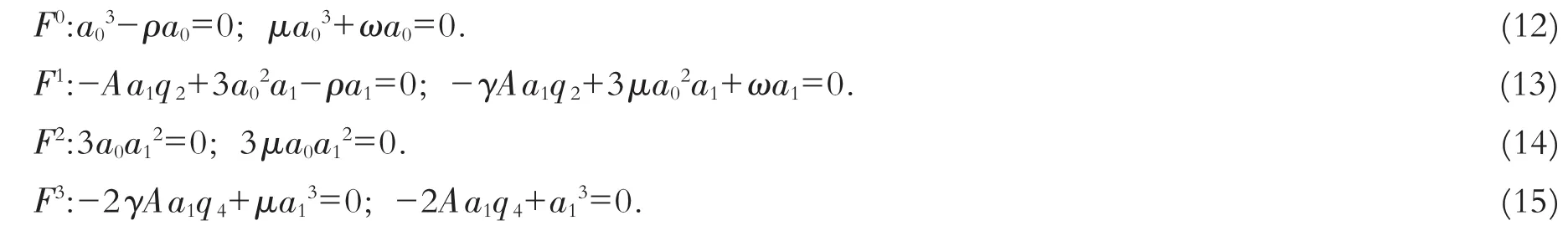
解方程(12)～(15)得到

2 解的情况

当q0,q2,q4取不同的值时，由(8)得到方程(1)的解如下(Jacobi椭圆函数)：

当q0＝1,q2＝－(1＋R2),q4＝R2时，F(ξ)＝sn(ξ,R)(模为R的椭圆正弦函数)是常微分方程(8)的解，则将该解代入(16)可得到(1)的解：

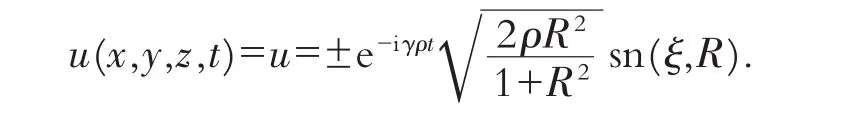
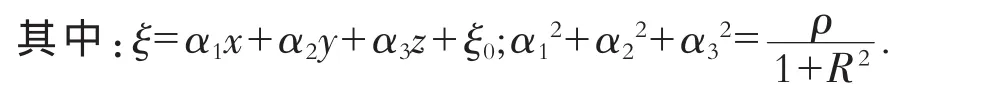
事实上，参照文献[8]中椭圆函数的定义方法，可以得到方程(8)更多的解.当q0,q2,q4取不同值时，可得到(1)的解，见表1.

表1 当q0,q2,q4取不同值时，方程(1)的解的情况

[1]FANG Fang,XIAO Yan.Stability of chirped bright and dark soliton-like solutions of the cubic complex Ginzburg-Landau equation with variable coefficients[J].Optics Communications,2006,268(12)：305-310.

[2]DAI Zhengde,LI Zhitian,LIU Zhenjiang,et al.Exact homoclinic wave and solition solutions for the 2D Ginzburg-Landau equation[J].Physics Letters A,2008,372(17)：3 010-3 014.

[3]DAI Zhengde,LI Shaolin,DAI Qingyun,et al.Singular periodic soliton solutions and resonance for the Kadomtsev-Petviashvili equation,Chaos[J].Solitions and Fractals,2007,34(4)：1 148-1 153.

[4]AKHMEDIEV N,ANKIEWICZ A.Solitons：Nonlinear Pulses and Beams[M].London：Chapman&Hall,1997.

[5]李栋龙，郭柏灵，刘旭红.三维复Ginzburg-Landau方程的整体解的存在唯一性[J].高校应用数学学报：A辑,2004,19(4)：409-416.

[6]ZHONG Penghong,YANG Ronghui,YANG Ganshan.Exact periodic and blow up solutions for 2D Ginzburg-Landau equation [J].Physics Letters A,2008,373：19-22.

[7]ZHOU Yubin,WANG Mingliang,MIAO Tiande.The periodic wave solutions and solitary wave solutions for a class of nonlinear partial differential equations[J].Physics Letters A,2004,323(1/2)：77-88.

[8]李志斌.非线性数学物理方程的行波解[M].北京：科学出版社,2007：142-146.

Some Exact Solutions to a Kind of 3D Complex Ginzburg-Landau Equation

LUO Senyue1,YANG Ronghui2,ZHONG Penghong3
(1.Department of Engineering Technology,Guangdong Radio and TV University,Guangzhou Guangdong510091,China; 2.Department of Mathematics,Yunnan Nationalities University,Kunming Yunnan650091,.China; 3.Department of Mathematics,Beijing University of Technology,Beijing100124,China)

By the method of auxiliary function together with the homogeneous balance principle,some exact periodic wave and kink wave solutions are obtained for a kind of 3D Complex Ginzburg-Landau equation.

Ginzburg-Landau;auxiliary function method;periodic wave;kink

O415

A

1009－8445（2010）02－0006－03

（责任编辑：陈静）

2010－01－10

罗森月(1982－)，女，广东清远人，广东广播电视大学助教，硕士.