熔化凝固问题的Keller盒式格式
赵妍,令锋
(1.内蒙古工业大学理学院,内蒙古呼和浩特010051;2.肇庆学院计算机学院,广东肇庆526061)
熔化凝固问题的Keller盒式格式
赵妍1,2,令锋2
(1.内蒙古工业大学理学院,内蒙古呼和浩特010051;2.肇庆学院计算机学院,广东肇庆526061)
建立了热参数依赖于温度的熔化凝固问题的显热容模型的Keller盒式格式,运用冻结系数法证明了该格式的无条件稳定性,并给出了数值算例.
显热容法;盒式格式;稳定性
数值求解熔化凝固问题的显热容模型[1]的控制方程具有强非线性性,其热参数是依赖于温度的函数.在数值求解中,发生相变的温度区间的选取对计算结果有较大影响.为克服这一缺点,1985年,Hsiao对显热容模型做了改进[2].Keller盒式格式是Keller在1970年提出的一种差分格式[3].1984年,Meek和Norbury用Keller盒式格式求解了非线性移动边界问题[4];2008年,Hamzah等给出了Keller盒式格式的并行算法[5].本文中,笔者在前人工作的基础上,对熔化凝固问题的显热容模型做进一步改进,用Keller盒式格式离散其控制方程,并分析该格式的无条件稳定性,最后给出数值算例.
1 显热容模型
根据显热容法,熔化凝固问题的控制方程可表示为

初始条件为

边界条件为

式中:

C(T)是依赖于温度的有界间断函数,Tm是相变临界温度.
2 Keller盒式格式

故Keller盒式格式的截断误差为R=O(τ2+h2).
文献[2]657-661的研究结果表明,直接应用式(4)会导致数值误差或解的不稳定性,为此,笔者依据文献[2]657-661的方法对热容量做进一步改进.由文献[2]657-661(见图1)知,在(i,j)点的热容量C(Ti,j)用(i-1,j),(i+1,j),(i,j-1),(i,j+1)4个点热容和的平均值来代替,即

依据同样的原理(见图2),在(j-1/2,n-1/2)点的热容量C(Tnj--11//22)用(j-1,n),(j,n),(j-1,n-1),(j,n-1)4个点热容和的平均值来代替,即

其中:Tn-1/2表示节点(j-1/2,n-1/2)处的温度,C(Tn-1/2,Tn)表示修正热容量.
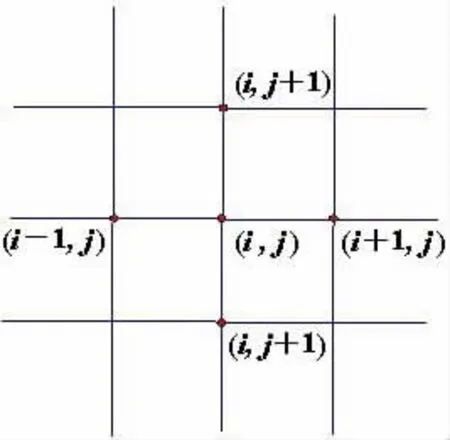
图1 改进的显热容法的节点示意图

图2 Keller盒式格式的节点示意图
3 Keller盒式格式的稳定性分析
定理1差分格式(12)是无条件稳定的.
证用“冻结系数”法[6]讨论其稳定性.
使用记号(7),将式(12)展开得

其中:λ=τ/h2.
令Tnj=vneikjh,代入式(15)得
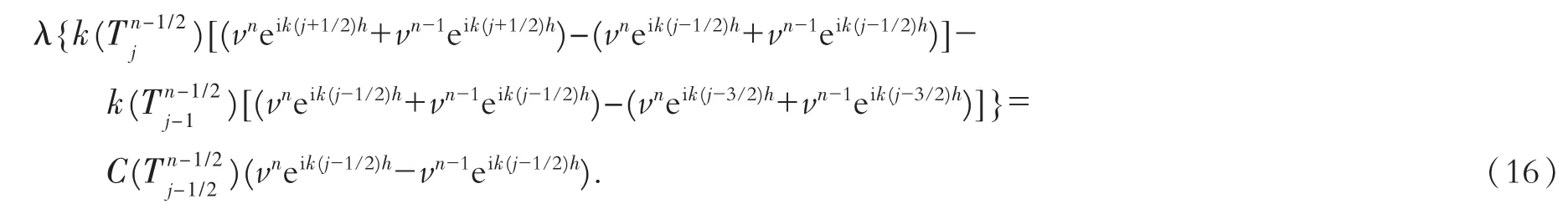
将式(16)整理后得

4 数值算例
为验证本文算法的有效性,以下用Keller盒式格式求解存在解析解问题[7](18)~(21)的数值解:

其解析解为

由积分公式及式(18)与(19),式(21)中的第2式可以写为如下形式:




控制方程(25)定义在固定边界0<σ<1,0<τ<H上.
边界条件(19)变形为

初始条件(20)变形为

边界条件(21)中的第1式变形为

式(23)变形为

利用Keller盒式格式,控制方程(25)可以写为如下形式:

控制方程(30)离散为下列2个差分方程:

在σ=0处的边界条件可近似表达为

初始条件(27)离散为

边界条件(28)离散为

对两相界面的守恒条件(式(29))应用矩形公式,得

求解方程组(31)~(36)时,取Δσ=0.01,Δτ=0.05,N=100,H=5,J=100.
迭代过程的一般步骤如下:
1)先给出试探的s(τn+1);
2)用TDMA算法求解方程(31)~(35),求得vnj+1,unj+1(j=0,1,2,…,J-1);
3)根据求得的unj+1,由式(36)计算出新的s(τn+1);
4)用新的s(τn+1)重复步骤2),直到满足收敛条件


图3u(3,t)时数值解和精确解之差
图3 为点(3,t)的数值解和精确解之差.从图3中可以看出,本文得到的数值解非常接近于精确解,表明笔者提出的方法是求解熔化凝固问题的有效方法.
[1]BONACINA C,COMINI G,FASANO A,et al.Numerical solution of phase-change problems[J].Heat Mass Transfer,1973,16:1 825-1 832.
[2]HSIAO J S.An efficient algorithm for finite-difference analyses of heat transfer with melting and solidification[J].Numerical Heat Transfer,1985(8):653-666.
[3]KELLER H B.A new difference scheme for parabolic problems,in Numerical Solutions of Partial Differential Equations[M]. 2nd ed.New York:Academic Press,1971:327-350.
[4]MEEK P C,NORBURY J.Nonlinear moving boundary problems and a Keller box scheme[J].SIAM J Numer Anal,1984,21:883-893.
[5]HAMZAH N,ALIAS N,AMIN N S.The parallelization of the Keller box method on heterogeneous cluster of workstations[J]. Journal of Fundamental Sciences,2008(4):253-259.
[6]陆金甫,关治.偏微分方程数值解法[M].2版.北京:清华大学出版社,2004:57-59.
[7]FURZELAND R M.A comparative study of numerical methods for moving boundary problems[J].J Inst Maths Applics,1980, 26:411-429.
Keller Box Scheme for Melting and Solidification Problem
ZHAO Yan1,2,LING Feng2
(1.College of Sciences,Inter Mongolia University of Technology,Hohhot Inter Mongolia010051,China; 2.School of Computer Science,Zhaoqing University,Zhaoqing Guangdong526061,China)
The Keller box scheme for the mathematical model of melting and solidification problem with temperature-dependent heat parameters is established.The unconditional stability of the scheme is analyzed by using the freeze coefficient method.And a numerical example is presented.
apparent heat capacity method;Keller box scheme;stability
O241.82
A
1009-8445(2010)02-0001-05
(责任编辑:陈静)
2009-10-09
广东省自然科学基金资助项目(04011600)
赵妍(1983-),女,黑龙江哈尔滨人,内蒙古工业大学与肇庆学院联合培养硕士研究生.

