基于极值响应面法的柔性机构可靠性优化设计

张春宜,白广忱,向敬忠

(1.北京航空航天大学 推进系,北京 100191;2.哈尔滨理工大学 机械动力工程学院,黑龙江 哈尔滨 150080)

工程设计问题中,设计变量和参数具有随机性,或约束中含有概率约束的优化设计,称为概率优化设计或可靠性优化设计[1].目前,结构系统的可靠性优化设计方法已经比较成熟[2-4],机构可靠性优化设计的研究相对较少.因为机构在运动过程中产生不断变化的惯性力,所以进行可靠性分析和优化设计时,在每一时刻,把机构看成瞬时结构,在此基础上进行可靠性分析和优化设计.显然,这比结构可靠性优化设计复杂得多[5-11].

柔性机构的动力学方程为二阶微分代数混合方程组,具有严重非线性、强耦合以及时变等特点,无法得到解析解,其可靠性分析极限状态方程也无法表示为具体的解析形式[1],这使得以可靠性为约束或者以可靠性为目标的柔性机构可靠性优化设计无法进行.要解决这个问题,必须首先解决柔性机构可靠性分析分方法问题.然现有的研究[12-14]只是停留在柔性机构可靠性分析方法和柔性机构优化设计上,柔性机构可靠性优化设计的研究很少见到,只有于霖冲进行了探索性研究[1].

本文在传统方法进行柔性机构截面尺寸初步设计的基础上,建立柔性机构可靠性优化设计的通用均值模型(meanmodel).并对其进行了实例仿真.

1 柔性机械可靠性分解

1.1 柔性机构动力学基本方程

由柔性多体动力学[15]可知,柔性机构的动力学方程为式中：q(t)为广义坐标,M为质量矩阵,K为刚度矩阵,Qk(t)为驱动力矩的广义力,Ug为系统的重力势能.

1.2 柔性机构可靠性分析极值响应面法的基本原理

在式(1)所示的柔性机构动力学方程中,将构件材料的强度、弹性模量、密度、截面尺寸作为输入随机变量,并设其符合正态分布,用 MCM对输入随机变量抽样,然后针对每组抽样求解动力学微分方程,得到与输入样本对应的柔性机构构件在[0,T]时域内的位移、速度、加速度响应,在此基础上求出其在[0,T]时域内对应的动态挠度(或动态应力)响应.

设某构件第 j组抽样输入样本为 X(j)=[x(j)1x(j)2…… x(j)n]T,在[0,T]时域内的输出响应为y(j)(t,X(j)),该响应在[0,T]时域内的最大值为y(j)max(X(j)).将不同输入样本在各自运动时域响应的最大值 y(j)max(X(j))构成的集合作为新的输出响应,则各组输入样本 X(j)与由输出响应的最大值y(j)max(X(j))的集合构成的新的响应函数：

之间可以建立起函数关系：

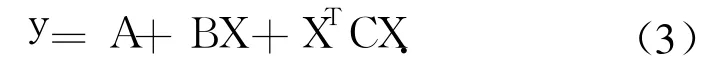
这种函数关系叫做极值响应面函数.由极值响应面函数确定的反应输入输出关系的曲线称之为极值响应曲线.其中,Z+为正整数.

1.3 柔性机构可靠性分析极值响应面法的数学模型

设 X(j)为第 i构件第 j个样本点输入随机向量,为对应的输出响应,Bi为一次项系数向量,Ci为二次项系数矩阵,Ai为常数项,构造极值响应面函数如下：

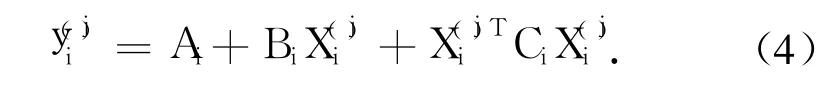
其中

式中：j=1,2……M;i=1,2…… n.M为样本点数;n为系统构件数;k为输入随机变量数.

在求解极值响应面函数系数时,先由 MCM小批量抽样,对每组样本在[0,T]时域内用数值法求解动力学微分方程,从中得到各组输入样本在[0,T]时域内输出响应的极值点,选取足够样本点数确定极值响应面函数的系数 Ai、Bi、Ci,得到极值响应面函数的确切表达式.

2 柔性机构可靠性优化设计基本理论

2.1 设计基本思想

柔性机构可靠性优化设计的难点在于其可靠性分析的极限状态方程不能表示为具体的显式形式.为了解决这个问题,首先用传统方法进行柔性机构截面尺寸的初步设计.其次将模态综合法与柔性多体系统动力学相结合,建立柔性机构的动力学微分方程.然后用蒙特卡罗法抽取输入参数随机样本,对每个抽样求解动力学微分方程,得到对应的位移、速度、加速度在分析时域内的动态响应.在此基础上求出对应的动态挠度(或应力)响应.将不同输入样本对应的变形(或应力)输出响应在分析时域内的最大值的全体作为新的输出(极值)响应,构造极值响应面函数,并确定极值响应面函数的系数.对极值响应面函数用一次二阶矩法,将可靠性指标表示为设计变量的函数.以材料密度、弹性模量、许用刚度、构件截面尺寸等为随机变量,以可靠性指标为约束函数,以机构质量为目标函数,以构件截面尺寸均值为设计变量,建立柔性机构可靠性优化设计的通用均值模型(mean model)并进行优化求解.由于柔性机构各构件的运动相互耦合,一个构件的尺寸变化会对其它构件产生影响.所以优化一般不可能一次达到目的,要循环几次进行优化.在一次优化完成后,进行可靠性计算检验,如果可靠性不满足要求(通常表现比设计要求的可靠性高)则要再次构造极值响应面函数,进行优化设计,这一过程通常要进行几次,直到优化设计后机构的可靠性与设计值之差达到给定值为止.

2.2 柔性机构构件刚度可靠性分析数学模型

设第 i构件截面尺寸为 xi1、xi2,长度为 xi3,材料密度为 ρi,材料的弹性模量 Ei为随机变量,且服从正态分布;由于相对各个构件长度均值而言,构件长度标准差非常小,因此可将长度视为确定量.另外,在实际工程中,检测变形是否满足要求时,检测工具的制造存在误差,测量过程中也存在误差,所以每次测量值也是随机变量.设第 i构件许用挠度 RYi,且服从正态分布,在分析周期内不考虑材料强度、密度、弹性模量等性能参数随时间变化.由极值响应函数(3)确定的构件中点变形极值响应为 yi,令 Zi=RYi-yi,做变换：

则第 i构件的刚度可靠度为

2.3 柔性机构刚度可靠性分析数学模型

由于机构系统是串联系统,所以整个系统的刚度可靠度[16]为

式中：n为系统的构件数.

2.4 柔性机构构件刚度可靠性优化设计模型

设第 i个构件的刚度可靠性指标为 βi.若按各构件等可靠度原则,n个构件中任一构件的可靠度和可靠性指标分别为

以可靠性指标为约束函数,以机构质量为目标函数,以构件截面尺寸为设计变量的柔性机构构件刚度可靠性优化设计均值模型[4]为

式中：gi[X(t)]=0为设计变量应该满足的其他等式约束;a、b为设计变量的上、下边界.将相关各量用设计变量表示,得到以设计变量表示构件中点最大变形表达式,对该式用一次二阶矩法,求得用设计变量均值 μxj1、μxj2和方差 σxj1、σxj2,(σxj1=vxμxj1、σxj2=vxμxj2,vx为设计变量变异系数)表示的构件中点变形的均值 μyi和方差 σyi,将该均值和方差代入式(13),得到以设计变量均值表示的柔性机构刚度可靠性优化设计均值模型,设计变量变异系数 vx可根据构件的加工精度公差要求和可靠性要求确定.

2.5 柔性机构整体刚度可靠性优化设计模型

以刚度可靠性指标为约束函数,以机构质量为目标函数,以构件截面尺寸均值为设计变量的柔性机构刚度可靠性优化设计均值模型[4]为

用设计变量表示的可靠性优化设计均值模型的求解非常困难,无法得到解析式,须用数值法求解,以此最优解作为该构件的截面尺寸,则该构件的质量最小.对机构中每个构件进行优化,则机构在满足可靠性要求的条件下质量最小.

3 算例分析

柔性机械臂的简化模型如图1所示.设柔性机械臂的两构件为均质欧拉梁,假定关节及臂端负载为集中质量,不考虑电机转子的转动惯量和电机的阻尼.构件 1在动坐标系 y1-x1中的纵坐标为y1(t,x1)、横坐标为 x1;构件 2在运动坐标系 y2-x2中的纵坐标为 y2(t,x2),横坐标为 x2,t为运动时间;动坐标系的横坐标在沿着各构件两端点的连线上,纵坐标即为构件的弹性变形.两动坐标系的运动由各自的方位角 θ1(t)、θ2(t)来描述.

图1 双连杆柔性机械臂简图Fig.1 Two-link flexible robotmanipulator

本例的传统设计结果如下[15]：两构件长度为l1=0.75m,l2=0.75m;构件 1、2端部分集中质量m1=5.5 kg、m2=2.75 kg,,构件 1、2驱动力矩为 τ1(t)=215sin3(2πt)-62 N◦ m、τ2(t)=75sin3(2πt)+15N◦m.优化设计前,材料参数信息如表1,各构件截面尺寸信息如表2.

将柔性机械臂的材料强度、弹性模量、密度、截面尺寸作为随机变量,并设其符合正态分布,而且相互独立.由于相对于长度均值而言,长度方差很小,所以本例将长度视为确定量.现在要求在各构件许用挠度均值为 0.018m,均差为 0.000 36 m时的可靠度为 0.954的情况下使得机构的质量最小,设计该柔性机械臂的截面尺寸.

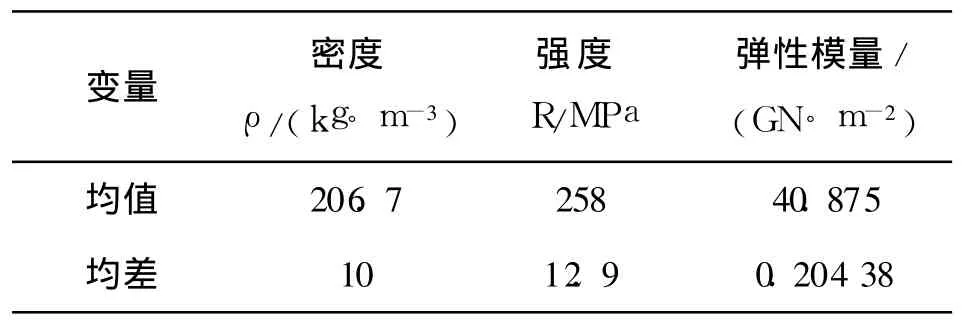
表1 构件 1和构件 2的材料参数Table 1 Materia l parameters o f No.1and 2

表2 构件 1和构件 2的截面尺寸Table 2 Section sizes of No.1 and 2 m

设两臂初始时刻均处于水平位置,且变形和速度为零,即 t=0时,q(0)=0,◦q(0)=0.求解本例构件中点变形极值响应面法函数时,n=2,M=9,k=4,则

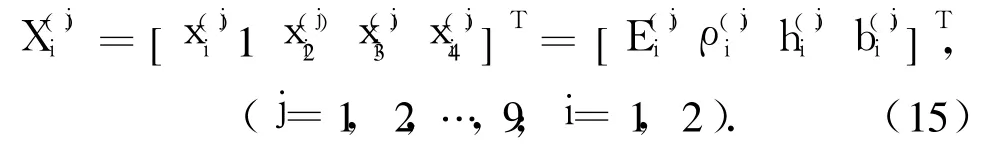
式中：E(j)i第 i构件材料弹性模量的第 j次抽样,ρ(j)i为第 i构件材料密度的第 j次抽样,h(j)i为第 i构件截面高的第 j次抽样,b(j)i为第 i构件截面宽的第 j次抽样.

以传统设计尺寸为设计初值,根据构件样本点输入随机变量及变形输出响应的各组数据求得的构件中点变形极值响应面函数系数如表3和表4,将求得的构件中点变形极值响应面函数系数分别代入式(12),分别得到各构件中点变形极值响应面函数的具体表达式.对该表达式用一次二阶矩法,将两构件中点变形极值响应的均值和方差 μyi,σyi表示为设计变量 xi1、xi2(i=1,2)的函数,锁定截面积的长宽比为 4∶1,代入式(13)(表达式冗长不便写出)用数值法进行优化求解结果如表5.

表3 构件 1的变形极值响应面函数系数Table 3 Coefficients in ERSF about deformation of No.1

表4 构件 2的变形极值响应面函数系数Table 4 Coefficients in ERSF about deformation of No.2

表5 设计变量值比较Table 5 Design variables comparison cm

4 结束语

本文在柔性机构复杂的动态响应与输入随机变量之间建立了比以往任何方法都简单的函数关系——极值响应面函数,并应用于柔性机构可靠性优化设计,本文实例中,机构质量比优化前减少 8.23%.为了研究方便作了一些假设.例如,假设各输入随机变量服从正态分布等.这会给计算结果带来误差,但是不影响方法的有效性.另外,本文只进行了柔性机构及其构件尺寸的可靠性优化设计,没有涉及可靠性分配优化问题.由于柔性机构的失效主要是变形超过范围失效,所以只进行了柔性机构刚度可靠性优化设计的实例计算,但是该思想和方法同样适用于柔性机构强度可靠性优化设计,也可以进行柔性机构强度可靠性与刚度可靠性综合优化设计.

[1]于霖冲.柔性机构动态可靠性分析、设计与仿真[D].北京：北京航空航天大学,2006：141-144.YU Linchong.Dynamic reliability analysis,design and simulation of flexib le mechanism[D].Beijing：BeiHang University,2006：141-144.

[2]KAYMAZ I,MCMAHON C,MENG X.Reliability based structural optimization using the response surface method and Monte Carlo simulation[C]//8th InternationalMachine Design and Production Conference.Ankara,Turkey：METU Printing Office,1998：459-468.

[3]PAPADRAKAKIS M,LAGAROS N D.Reliability based structural optimization using neural networks and Monte Carlo simu lation[J].Computer Methods in Applied Mechanics and Engineering,2002,191(32)：3491-3507.

[4]刘善维.机械零件的可靠性优化设计[M].北京：中国科学技术出版社,1993：239-242.

[5]陈建军,陈勇,崔明涛,等.基于运动精度可靠性的平面四杆机构优化设计[J].机械科学与技术,2002,21(6)：940-943.CHEN Jianjun,CHENYong,CUIMingtao etal.Optimization design for flat four-barmechanismbased on reliability of kinematics accuracy[J].Mechanical Science and Technology for Aerospace Engineering,2002,21(6)：940-943.

[6]张义民,黄贤振,张旭方,等.不完全概率信息牛头刨床机构运动精度的可靠性优化设计[J].中国机械工程,2008,19(19)：2355-2358.ZHANG Yimin,HUANG Xianzhen,ZHANG Xufang,et al.Optimization design for kinematics accuracy reliability of shapingmechanismunder incomplete probability information[J].China Mechanical Engineering,2008,19(19)：2355-2358.

[7]张义民,黄贤振,贺向东.不完全概率信息牛头刨床机构运动精度可靠性稳健设计[J].机械工程学报,2009,45(4)：105-110.ZHANG Yimin,HUANG Xianzhen,He Xangdong.Reliability-based robust design for kinematics accuracy of the shapermechanismunder incomplete probability information[J].Journal of Mechanical Engineering,2009,45(4)：105-110.

[8]李明喜.机构运动的模糊可靠性优化设计[J].河南科技大学学报：自然科学版,2003,24(2)：107-110.LIMingxi.Optimumdesign of fuzzy reliability for mecha-nismmotion[J].Journal of Henan University of Scince and Technalogy,2003 24(2)：107-110.

[9]张春宜,白广忱.运动机构强度可靠性优化设计[J].机械强度,2009,3：396-400.ZHANG Chunyi,BAIGuangchen.Optimization on strengthreliability ofoperatingmechanism[J].Journal of Mechanical Strength,2009,3：396-400.

[10]MARCELIN J L.Usinggenetic algorithms for theoptimization ofmechanisms[J].The International Journal of Advanced Manu facturing Technology,2005,27(1-2)：2-6.

[11]YOUN B D,CHOIK K.A newresponse surfacemethodology for reliability based design optimization[J].Computers and Structures,2004,82(2-3)：241-256.

[12]于霖冲,白广忱,焦俊婷.柔性机构动态强度可靠性分析理论和方法研究[J].机械强度,2007,29(6)：956-959.YU Linchong,BAIGuangchen,JIAO Junting.Research on dynamical strength reliability analysis theory and methodology of flexiblemechanism[J].Journal of Mechanical Strength,2007,29(6)：956-959.

[13]杨鑫,袁茹,王莉.基于ANNMC方法进行弹性机构的动态强度可靠性分析[J].机械科学与技术,2008,27(4)：462-465.YANG Xin,YUAN Ru,WANG Li.Dynamical strength reliability analysis of a flexible mechanismusing neural networks[J].Mechanical Science and Technology for Aerospace Engineering,2008,27(4)：462-465.

[14]张建国,刘英卫,郑冬青.弹性连杆机构可靠性分析方法研究[J].机械科学与技术,2001,20(2)：247-248.ZHANG Jianguo,LIU Yingwei,ZHENG Dongqing.The reliability analysismethod of elastic linkage[J].Mechanical Science and Technology for Aerospace Engineering,2001,20(2)：247-248.

[15]陆佑方.柔性多体系统动力学[M].北京：高等教育出版社,1996：165-180.

[16]何水清,王善.结构可靠性分析与设计[M].北京：国防工业出版社,1993：198-199.