R树的方向查询精过滤方法

张泽宝,张健沛,李若愚

(哈尔滨工程大学 计算机科学与技术学院,黑龙江 哈尔滨 150001)

在空间数据库中,每一个空间对象都有一个与其相对应的空间坐标,空间坐标不仅可以表示对象在空间中的位置信息,而且根据空间坐标可以引申出对象之间的空间关系这一重要概念.空间对象之间的空间关系主要分为 3大类：距离关系、拓扑关系和方向关系.在基于拓扑关系的查询方面,KOTHURIR等提出了中间过滤方法,对候选结果集进行 2次过滤[1].BADAWY W等提出利用启发式信息来进行过滤[2].Rousspoulos[3]等利用测量距离对 R-树[4]的搜索过程中进行有效的剪枝.国防科技大学的肖予钦[5]等人,定义了一个四元组模型的方向关系,本文研究的出发点正是基于四元组模型.为了对复杂的空间数据进行高效的查询,包括 Oracle Spatial在内的许多数据搜索引擎都使用可分为两步的查询过滤方法.第 1步被称为过滤,使用几何数据的外部近似(如 MBR),外部近似完全包含几何数据,过滤通常是利用空间索引[6]来进行的.在第 2步的取精过程中,候选数据与查询图形进行精确计算,得出最终的结果集返回给用户,这步是空间连接查询[7]耗时的.

1 方向关系定义

1.1 MBR之间的方向关系

为了提高空间数据的查询效率,空间对象通常都是由 MBR来近似表示的.本文所给出的方向关系是基于四元组模型的：假设坐标系 y轴与 north方向一致,x轴与 east方向一致,两个空间对象的 MBR分别为 a和 b,一个矩形完全可以由其左下角顶点(axl,ayl)和右上角顶点(axu,ayu)来唯一确定.2个MBR之间的方向关系完全可以由其在某一坐标轴上的投影来确定.采用(N,S)a,b和(E,W)a,b,分别表示 North-South方向和 East-West方向上 a相对于 b的方向关系,(N,S)a,b,和(E,W)a,b定义如下：

在实际计算中,a和 b在 X轴上的投影之间的关系决定了(E,W)a,b的取值,下图为(E,W)a,b定义的直观解释,(N,S)a,b同理可知,如图1所示.

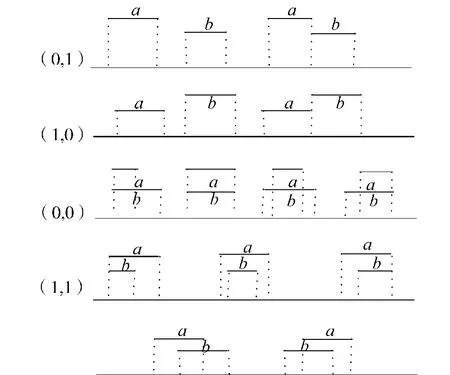
图1 a,b在 X轴投影间的关系Fig.1 Relationships between projections of a and b on X-axis

由(N,S)a,b,和(E,W)a,b排列最合可以得到四元组模型 (N,S,E,W)a,b,比如：NorthWest(a,b),其取值为 (1,0,0,1),其他的类似可知.

1.2 对象之间的方向关系

由于 MBR只是空间对象的近似表示,所以MBR之间的方向关系并不一定就是空间对象之间的方向关系.方向关系矩阵根据目标对象落在参考对象内对空间的不同划分来描述方向[8-10].参考对象把空间划分为 9个部分：NorthWest(NW),North(N),NorthEast(NE),West(W),Same(O),East(E),SouthWest(SW),South(S)和SouthEast(SE).其表示方法如下所示：

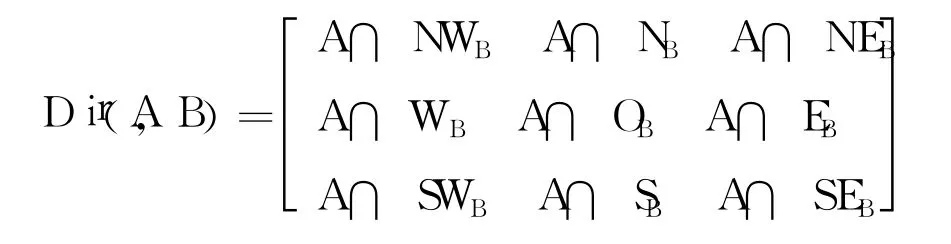
它是一个 3×3的矩阵,其元素保存了空间划分间的相邻关系及目标对象和参考对象间的相交情况.其中元素 0表示不相交,元素 1表示相交,若目标对象和参考对象的某个空间划分相交,则它们满足相应划分所定义的方向关系.

在具体实现中,采用位段[NwN NE wO E SwS SE]来存储方向关系矩阵,即矩阵中每个元素都用 1位表示,这样可以极大地减少存储空间.如[0 0 1 0 0 0 0 0 0]表示目标对象在参考对象的东北方向,[0 0 0 0 0 0 0 1 1]表示目标对象在参考对象的南和东南方向,对于方向关系矩阵中每个元素取值的判断,采用几何计算中多边形相交的算法就可以解决.

2 方向关系查询处理方法

R-树有一个非常重要的特性,那就是 R-树中任一结点所表示的空间区域必定包含其所有子结点的空间区域,正是因为 R-树具有此特性,因此可采取文献[5]的剪枝策略对其进行 R-树剪枝.在空间对象的查询过程中,其实质上就是 R-树的一次遍历过程,为了达到提高对空间对象的查询效率的目的,本文采取了一种剪枝策略,在遍历过程中,采取一定的剪枝方法来避免搜索那些肯定不在目标结果范围内的结点,使得访问结点分支的数量减少.根据 R-树的这个特性,可以得到下面的剪枝策略.如 R-树中的 2个结点之间满足 {NorthEast,NorthWest,South-East,SouthWest}中的任一关系,那么两结点的所有子孙结点也必定满足相应关系.

若 2个结点满足 {NorthSame,NorthUnknown}中的任一关系,那么这 2个结点的子结点必定满足如下 4种关系 {NorthEast,NorthWest,NorthSame,NorthUnknown}之一,其他对象之间的空间关系可以类推得到,因此要查找所有满足 NorthWest关系的空间对象,那么在遍历 R-树的过程中,只需要访问那些中间结点满足{NorthWest,NorthSame,NorthUnknown,SameWest,UnknownWest,SameSame,SameUnknown,UnknownSame,UnknownUnknown}中任一关系才可能得到正确的查询结果,而最终搜索到的 2个对象的 MBR之间的关系必须满足{NorthUnknown,NorthWest,UnknownUnknown,UnknownWest}之一.显然,这样就避免了访问那些肯定不在目标结果范围内的中间结点,从而提高了空间对象的查询效率.

本文在以上的剪枝策略定义基础上,在过滤步骤和求精步骤之间,插入了一个中间步骤,通过这个中间步骤,对查询对象进行 2次过滤以减少候选集的大小,因此可以很大程度上降低求精步骤的计算代价,通过理论的分析,证明改进之后的查询处理方法具有更高的效率,也通过实例验证了改进的方法可提高查询处理性能,具体的查询处理过程如下.

定义中如果一维的空间关系确定,另外一维方向需要精算来确定空间关系,如：NorthUnknown,UnknownWest,SameUnknown,UnknownSame,UnknownEast,SouthUnknown.如果得出两对象之间的方向关系为 NorthUnknown,那么就可以推断出 2个实际空间对象 a和 b之间的方向关系必定满足{NW(a,b)∧ N(a,b),NW(a,b)∧ N(a,b)∧NE(a,b),N(a,b)∧ NE(a,b)}其中之一,如图2所示.

从图2可以很明显的看出只需要根据目标对象的顶点落在哪一个划分区间中,即可判断出 2个实际对象之间的空间关系并且得到 2个实际对象之间的方向关系矩阵.例如对于图2(b),可以很容易的计算出 a对象的 MBR的左上角顶点和右上角顶点分别落在划分 NW和划分 NE中,从而可得出 a相对于 b的空间关系矩阵为[1 1 1 0 0 0 0 0 0],因而无需再进行大量极其复杂的精确几何计算,所以极大地提高了查询效率.其他情况可以类推得到.

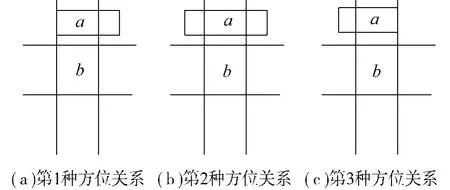
图2 二维举例Fig.2 Example on two dimensions

3 精过滤查询处理方法

由于 MBR性质和特点可以得到如下的引理.

引理 1 对于 R-树中非叶子结点的 MBR,任一MBR的每一个面都至少包含其内部空间对象的一个点.如图3所示.

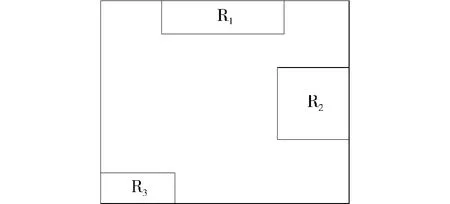
图3 非叶子结点举例Fig.3 Example on nonleaf node

证明 由 R-树定义显然可得.

引理 2 在二维空间中,对于 R-树中叶子结点的 MBR,任一 MBR都至少有两个边包含其内部空间对象的一个点.如图4所示.

证明 由 MBR定义显然可得.

当在两维方向上均不能确定对象之间的方向关系,也就是两对象之间 MBR的方向关系满足 UnknownUnknown.由方向关系的定义可以得出 UnknownUnknown一共有 25种组合情况,这是因为每一个 Unknown都是由 5种情况组合而成的.而这 25种情况根据对象a的 MBR所占据的划分个数不同,可以分成 3个大类.如图5所示.

第1大类一共有16种情况所组成,对象 a的MBR占据 4个划分,如图5(a)所示.

第2大类一共有8种情况所组成,对象 a的MBR占据 6个划分,如图5(b)所示.

第3大类只有1种情况所组成,对象 a的 MBR占据 9个划分,如图5(c)所示.

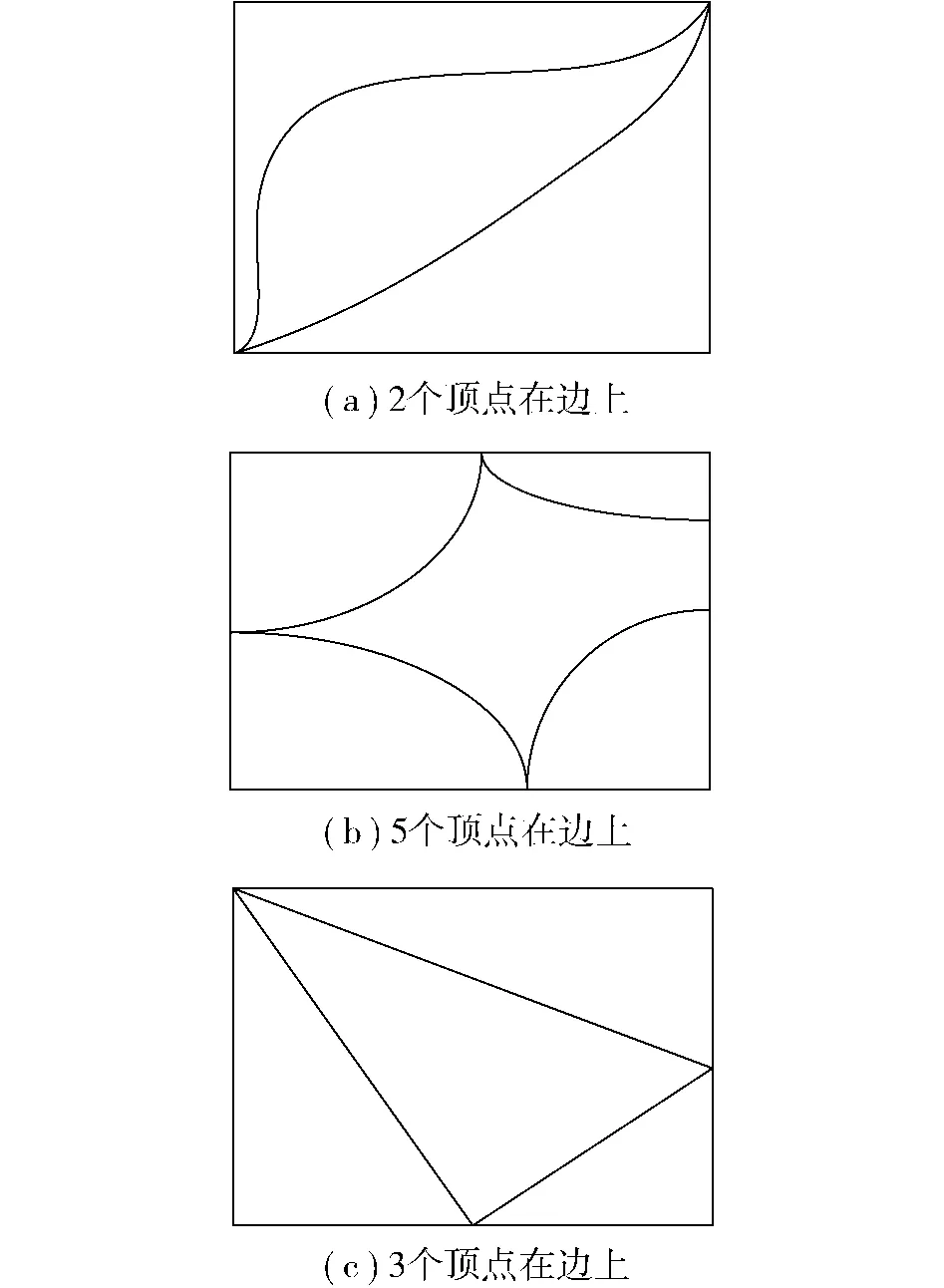
图4 叶子结点举例Fig.4 Example on leaf nodes

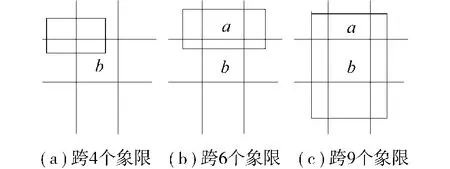
图5 3类情况举例Fig.5 Example on three classes

根据引理 2可以得到空间对象 a与其 MBR至少交于 2点,如果可以确定空间对象与其 MBR的相交点,根据相交点所处的划分就可以很容易的判断出实际空间对象有一部分区域必定落在该划分之中,所在精算步骤中可以排除在该划分中的计算,从而大大减少了计算代价.

相交点的计算是十分简便的,因为根据MBR的定义和引理 2可知,在求解空间对象的 MBR的同时也会得到空间对象与其 MBR的相交点,当求出相交点之后,即可得出空间对象必定落在某个划分之中,从而无需复杂的取精操作,而对于剩下的划分,需要做的只是把对象 MBR和该划分的交集(必定为一个矩形)与空间对象进行比较,看其是否落在该交集之内,这就将两个空间对象的计算问题转化为了一个窗口查询的问题,相对于计算 2个空间对象之间的关系,窗口查询的效率更高,所付出的代价更小.

本文在传统的过滤方法过程中加入了一个中间步骤,通过理论推导可以得出,对传统方法改进之后算法的性能得到了很大的提升.

证明过程：本文算法假设,某一种情况在单个象限上进行取精操作的权值为 1,而各个空间对象是服从均匀分布的.根据每种情况出现的次数和概率进行证明,下面为其证明过程,其中传统的查询过滤方法为 TQFM,改进的查询过滤方法为 IQFM.

TQFM方法：

1)在两个方向上均需要执行取精操作的是(UnknownUnknown)的情况,在传统定义中有 5种空间位置关系被定义为 Unknown,而每种情况均需要在各个象限上进行取精的操作,所以在 UnknownUnknown情况下的算法耗费为 121,即

第 1大类：16×4=64

第 2大类：8×6=48

第 3大类：1×9=9

所以总耗费为：16×4+8×6+1×9=121.

2)仅在单个方向上进行取精操作的有：(Same-Unknown,UnknownSame,NorthUnknown,SouthUnknown,UnknownWest,UnknownEast)6种关系谓词,每一种谓词对应了 3种情况,如图2所示,3种情况共需要在 7个划分上进行精算操作,所以在单个方向精算的耗费为 42,即

6×(2+2+3)=42.

TQFM方法的总耗费为：121+42=163.

IQFM方法：

由引理 2可知,空间对象与其 MBR至少有 2个相交点,在这里假设最坏的情况,即每一个空间对象与其 MBR有 2个相交点,也就是可以确定空间对象存在于某 2个划分之中,从而减少 2个划分的求精计算.

1)在 2个方向上都需要执行取精操作

(UnknownUnknown)：

第1大类：16×(4-2)=32

第2大类：8×(6-2)=32

第3大类：1×(9-2)=7

所以总耗费为：16×2+8×4+1×7=71.

2)在单个方向上无需进行取精操作(因为通过判断对象在某一维上的极值点落在哪一个划分内,即可确定其跨越的划分情况,同时其 9元组也随之得到 )：(SameUnknown,UnknownSame,NorthUnknown,SouthUnknown,UnknownWest,UnknownEast).

IQFM方法的总耗费为：71+0=71.

由上可得：IQFM/TQFM=43.5%,改进的方法需要精算的算法耗费仅为传统方法的 43.5%,减少了大量的精算数据集,性能得到了很大的提升.

4 实验设计与性能评估

4.1 实验环境

前面已经理论分析论证了算法的有效性,现在通过实验来对算法的性能进行评估.实验平台：

操作系统：Windows2 000 Professional

CPU：1.70GHz

内存：256M

编程环境：Visual C++6.0

4.2 实验示例与总结

在仿真实验中本文使用美国国家统计局所提供的 TIGER/Line图形文件[11],它是测试空间连接算法的标准数据集.TIGER/Line图形文件来自于美国国家统计局的 MAF/TIGER数据库,它包含了公路、铁路、河流等地理信息.TIGER/Line图形文件是对外公开并且是完全免费的,通常用来为地理信息系统(GIS)或绘图软件提供数字地图.本文选取哥伦比亚地区的道路和街区作为 2个输入数据集,前者包含 15 141个线对象,后者包含 5 665个面对象.本文为每个数据集创建了页面大小 1 kB的 R-树,叶结点存储的是对象的 MBR.

先来看一下在使用单个连接谓词情况下,使用改进的查询过滤方法(IQFM)与传统的查询过滤方法(TQFM)的性能比较,磁盘的访问次数和执行时间如表1所示.

表1 I/O访问次数和比较次数Table 1 Number of I/O and number of comparisons

接下来,看一下在综合情况下,使用改进的查询过滤方法与传统的查询过滤方法进行的性能比较,对比结果如图6、图7所示.其中,DT为 Disk Time,RT为 Response Time,QR为 Query Radius.

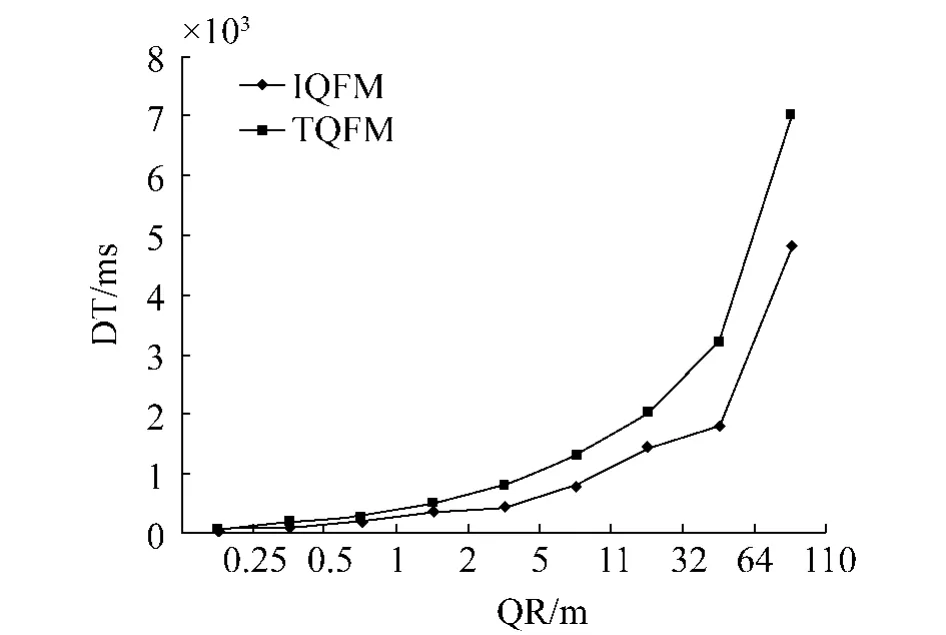
图6 I/O比较Fig.6 Comparison of I/O

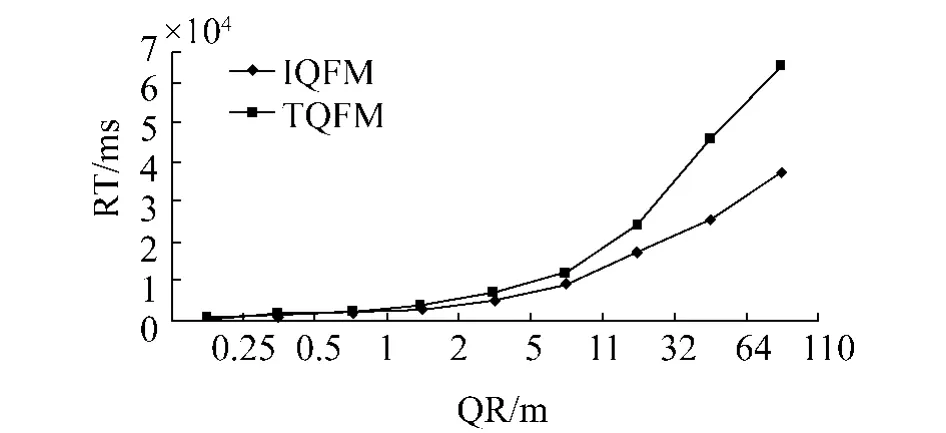
图7 执行时间比较Fig.7 Comparison of response time

图6和图7是针对磁盘的访问次数和算法的执行时间 2个重要的算法性能指标,这是衡量算法质量的两个重要因素.所以本文就将磁盘的访问次数和算法执行时间来分别作为实验结果的衡量标准.

图6的横坐标表示的是查询半径,纵坐标表示的是磁盘的访问次数.从图中可以明显的看到,当查询半径小于 0.5 km的时候,使用新的过滤方法与不使用新过滤方法相比磁盘的访问次数基本上是相同的,都在 47次左右.而当查询半径大于 1 km时,使用新的过滤方法对磁盘的访问次数要明显的小于不使用新的过滤方法.这主要是因为在查询半径比较小的情况下,查询范围内的目标对象也是非常少的,所以并不能很好的体现出两种方法之间的差异,而当查询范围逐渐增大的时候,范围内的目标对象也随之增多,新的过滤方法对查询性能的影响逐渐增大,所以新的过滤方法对磁盘的访问次数要明显的小于之前的方法,从而新的方法显示出了更好的查询性能.在图7中,之所以当查询半径小于 0.5 km时 2个算法的执行时间十分的接近,其原因上面已经解释过.所以,新的方法不仅仅是在理论上可行的,在实际中对空间查询也可以起到很好的优化作用.

5 结束语

对空间对象的方向关系模型进行了分析,根据在各坐标轴上的投影,分析对象之间的关系,给出了方向关系矩阵,分析了方向关系查询处理方法,给出了查询处理过程的剪枝策略,提出了一种新的查询过滤方法.该方法通过参考对象对空间进行划分,根据目标对象与其 MBR的交点是否落在某个划分中即可判断出该目标对象的具体位置,从而确定出目标对象和参考对象之间的多种可能的方向关系,通过此方法进行过滤,减少了精确计算的数据量.通过理论的分析和实际的试验表明,查询时间和磁盘访问的次数分别提高了 40%和 20%左右.

[1]KOTHURI R,RAVADA S.Efficient Processing of large spatial queries using interior approximation[C]//Proceedings of the 7th International Symposiumon Advances in Spatial and Temporal Database.Redondo Beach,CA,USA,2001：404-421.

[2]BADAWY wM,GAREF W.On local heuristics to speed uppolygon-polygon intersection tests[C]//Proceedings of the 7th International Symposiumon Advances in Geographic Information Systems.Kansas City,USA,1999：97-102.

[3]ROUSSPOULOS N,KELLY S,VINCENT F.Nearest neighbor queries[C]//Proceedings of the ACmSIGMOD International Conference on the Management of Data.San Jose,CA,USA,1995：71-79.

[4]GUTTMAN A.R-trees：a dynamic index structure for spatial searching[C]//Proc.of International Conference on Managementof Data.Boston,USA,1984：47-54.

[5]肖予钦,张巨,景宁,李军.基于R树的方向关系查询处理[J].软件学报,2004,15(1)：103-111.XIAO Yuqin,ZHANG Ju,JING Ning,LI Jun.Direction relation query processing using R-trees[J].Journal of Software,2004,15(1)：103-111.

[6]郭薇,郭菁,胡志勇.空间数据库索引技术[M].上海：上海交通大学出版社,2006：1-7.GUO Wei,GUO Jing,HU Zhiyong.Indexing techniques for spatial database[M].Shanghai：Shanghai Jiao Tong University Press,2006：1-7.

[7]李俊洁,郝忠孝.基于栅格的空间连接查询[J].哈尔滨理工大学学报,2008,13(2)：1-4.LIJunjie,HAO Zhongxiao.Spatial join query based raster signatures[J].Journal of Harbin University of Science and Technology,2008,13(2)：1-4.

[8]GOYAL R K,EGENHOFER mJ.Similarity of cardinal directions[C]//Proc of the SSTD 2001.Lecture Notes in Computer Science 2121.Berlin：Springer-Verlag,2001：33-55.

[9]曹菡,陈军,杜道生.空间目标方向关系的定性扩展描述[J].测绘学报,2001,30(2)：162-167.CAO Han,CHEN Jun,DU Daosheng.Qualitativeextension description for cardinal directions of spatialobjects[J].Acta Geodaetica et Cartographica Sinica,200l,30(2)：l62-167.

[10]冯玉才,陈琳,曹忠升.空间数据库的方向关系模型[J].计算机工程与应用,2001,20：115-l 17.FENG Yucai,CHEN Lin,CAOZhongsheng.Direction relation model of spatial database[J].Computer Engineering and Applications,2001,20：115-l 17.

[11]US Bureau of the Census.Census 2000 TIGER/Line files[EB/OL].(2000-08-05).http：//www.census.gov.