散乱点云切片数据快速获取与优化

孙永伟,孙殿柱,朱昌志,朱宗伟

(山东理工大学 机械工程学院,山东 淄博 255091)

随着三维数字化激光扫描技术的发展,逆向工程中处理的点云数据通常具有海量规模,且存在大量冗余信息,采用切片技术可在准确反映产品型面特征的同时,有效提高参数曲线、曲面的重构效率.目前通常将点云数据向距离最近的切片投影,获取投影数据作为切片数据.文献[1-2]通过对点云进行随机采样计算点云密度,由该密度确定切片位置.由于采样点的选取具有很大随机性,所得数据不能有效反映点云的型面特征,且采用 Christofides算法进行排序,时间复杂度达到 O(n4),算法运行效率低.文献[3-5]基于过点云两极值点的直线将切片数据分为两部分,根据点在直线上的投影对两部分数据分别排序,然后合并,得到有序的切片数据序列,并采用角偏差法和弦高差法对排序后的数据进行精简,该算法可克服文献[1-2]算法在点云数据处理方面效率低的问题,但只适用于没有重复投影点的切片点云,不能有效处理具有多重轮廓的复杂散乱点云数据.针对上述问题,本文采用 R*S树建立散乱点云动态索引,基于该索引快速获取切片位置与切片邻域数据,将切片邻域数据向切片投影获取切片数据,并为切片数据建立极坐标系.分别基于极角阈值与极径阈值实现切片数据区域划分与轮廓分离,通过依次连接各区域相同轮廓数据形心,获取精确有序的单轮廓或多轮廓切片数据.

1 切片数据获取

在切片数据获取过程中,可采用 R*S树[6-8]为散乱点云数据建立动态索引,以实现数据点的快速定位与准确查询,从而提高切片数据获取效率.例如对图1所示的散乱点云构建 R*S树动态索引,各层结点 MBR如图2所示,该结构由 3种结点组成,最上层为根结点,最底层为叶结点,其余为内部结点.除根结点外,每个结点的子结点数 n满足m≤n≤M,其中 m和 M分别为结点的最小、最大子结点数,通常可取 8和 20.

图1 点云数据Fig.1 Points data

图2 散乱点云的动态空间索引结构Fig.2 Spatial index structure of scattered points

基于散乱点云动态索引,采用深度优先遍历算法获取与切片相交的叶结点,依据叶结点与切片的位置关系确定下层切片的位置,并将叶结点包含的数据作为切片邻域数据,将邻域数据向切片投影获取切片数据.

假设切片平行于 xoy平面,法矢 n指向 z轴正方向.获取点云在 z轴上的最小值 zmin和最大值 zmax采用式(1)计算初始切片位置：

采用式(2)计算其余各层切片位置：

其中,εj为与切片相交的叶结点中各顶点到切片的距离,可由式(3)计算,n为与第 i层切片相交的各叶结点中位于切片正侧(即 εj＞0)的叶结点顶点数：

式中：v为与切片相交的叶结点 MBR的顶点.

切片位置确定后,令 V={vj|j=1,2,…,8}为叶结点 MBR的顶点集合,q为切片内的任意一点,根据式(3)判断叶结点与切片的位置关系,若 εj≤0,表示 vj位于切片的负侧,若 εj＞0,表示 vj位于切片的正侧.若索引结点 8个顶点的 εj同时为正(或负),表示结点与切片相离,否则相交.

基于上述原则,采用深度优先遍历方法,获取与切片相交的叶结点,将其包含的数据点作为该切片邻域数据,如图3所示,具体步骤如下：

1)输入 R*S树根结点;

2)若输入结点为叶结点,判断该结点与切片的位置关系,获取切片邻域数据;

3)若结点为根结点或内部结点,则循环获取当前结点的子结点,返回 2).

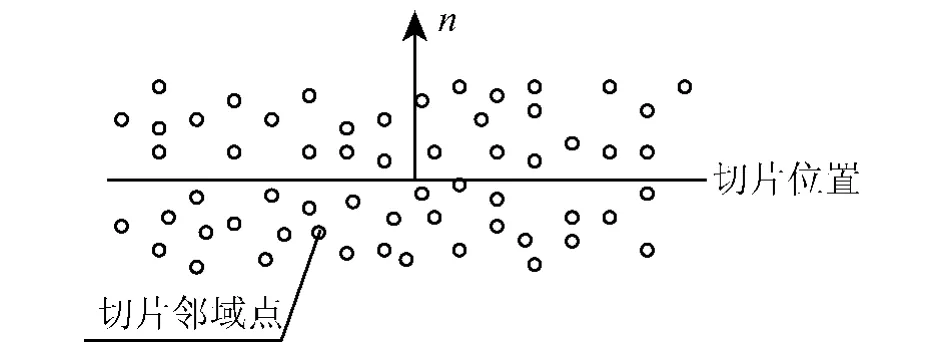
图3 切片邻域数据Fig.3 Slice neighborhood data

将获取的切片邻域数据向切片投影得到切片数据,如图4所示,将切片数据存储到序列 T={pi|i=0,1,2,…,n-1}中,n为 T中数据点的个数,pi=(xi,yi,zi).

图4 切片邻域数据投影点Fig.4 Projection points of slice neighborhood data

2 切片数据优化

投影法获取的切片数据为具有一定宽度的点云带,存在大量冗余数据,且切片数据之间没有明显的拓扑邻近关系,在保留截面特征数据点的同时对其进行精简与排序,实现切片数据的优化,以适用于参数曲线与曲面重构[9].

为实现切片数据精简,可将切片数据点转换至极坐标系下并将其划分为多个区域,对每个较小区域分别进行轮廓分离及特征数据提取,在保证数据信息完整性的同时实现切片数据的精简,然后依次连接各区域相同轮廓特征数据,得到精确有序的切片数据点序列.

T为切片数据点集合,该集合中数据点个数为n,采用式(4)计算 T中数据点中心坐标 O0：

如图5所示,以 O0为极坐标原点,以 O0为起点作一条平行于 X轴的射线,作为极轴,建立切片数据极坐标系,获取切片数据点极径 r及极角 θ.

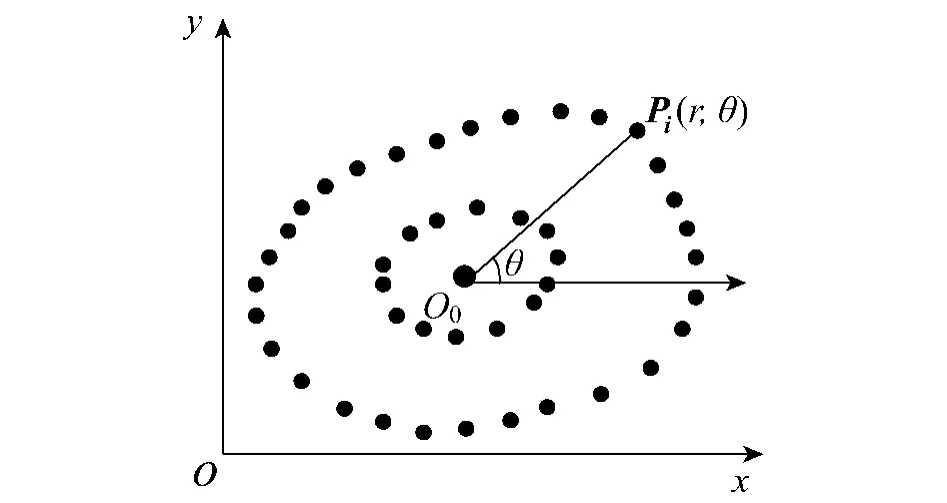
图5 切片数据的极坐标表示Fig.5 Polar of slicing data

根据散乱点云轮廓特征,所获取的切片数据可分为单轮廓与多轮廓切片数据,如图6所示,下面针对这 2种切片数据类型分别进行精简与排序处理.

2.1 单轮廓切片数据优化

对于单轮廓切片数据,轮廓形状较为简单,可对其进行极角区域划分处理,即基于切片数据极角,将切片数据划分为多个扇形区域.如图7所示,每个扇形区域的极角步长为 ρ,采用式(4)计算各区域切片数据形心,将其作为切片数据特征点,依次连接各区域特征点,所得序列即为优化后的切片数据点序列.

图7 切片数据区域划分Fig.7 Zoning of slicing data

2.2 多轮廓切片数据优化

多轮廓切片数据体现为：1)同一扇形区域内具有不同轮廓上的数据点;2)部分轮廓出现迂回现象,即同一轮廓数据在同一扇形区域多次出现.多轮廓切片数据优化具体步骤如下：

1)基于切片数据极角将切片数据划分为多个扇形区域,依次对各扇形区域数据进行如下操作：令该扇形区域数据集合为 S,任取 S中数据点 P,其极径为 rP,将 P加入临时序列 V,依次令 S中其他数据点为 P′,极径为 rP′,取极径阈值为 μ,若 |rP′-rP|＜μ,则将 P′加入序列 V,采用式(4)计算 V中数据形心,将 C加入集合 U.若 S=V,则返回,否则,令 S=S-V,置空集合 V,继续执行上述步骤.

2)取 U中任一数据点 C,其极径为 rC,将其添加到序列 M,C所在区域为 S.

3)依次令 S下一区域(取极角增大的方向为正方向)内形心点为 P,极径为 rP,若 |rC-rP|＜μ,执行 4),若不存在满足上述条件的形心点,说明该轮廓数据已经全部分离或者发生迂回,执行 5).

4)将 P加入序列 M中,令 P所在区域为 S,P为 C,rC=rP返回 3).

5)依次令 S上一区域内形心点为 P,极径为 rP,若 |rC=rP|＜μ,则将 P加入序列 M中,令 P所在区域为 S,P为 C,rC=rP,迭代执行该步骤.

6)若 U=M,程序结束,否则,令 Mi=M(i初值为 0),i=i+1,U=U-M,返回 2).

上述步骤基于极径阈值实现切片数据轮廓分离,以区域形心点作为数据特征点,并依次连接,实现切片数据的精简与排序,所得序列 Mi及 M中数据即为精确有序的切片数据点序列,可直接用于后续的曲线与曲面拟合.

3 算法时间复杂度分析

设散乱点云中数据点数为 n,本文算法时间复杂度分析如下：

1)设 R*S树动态索引各结点单元中最大子结点数为 M,树的层数,则建立散乱点云动态索引的时间复杂度为

2)基于散乱点云动态索引获取切片数据的过程分为 3步：切片位置的确定、切片邻域数据的获取及切片数据的计算,设切片层数为 k,获取切片数据的时间复杂度为 k(M+M2+… +ML-2)+8ML-2+

3)设切片数据的个数为 N,采用坐标法划分出的区域数为 k,则单层切片数据精简与排序的时间复杂度是其中 ni为第 i个扇形区域中数据点个数.

4 实例应用

采用本文算法和文献[4]算法对图6(a)所示切片数据进行处理,效果如图8所示,切片时间分别为：0.263和 0.351;表1、2分别为本文算法和文献[4]对切片数据处理后的误差分析计算结果,本文算法与文献[4]相比,绝对误差、负向偏差及正向偏差分别减少 55%、37%和 54%.由图8及表1、2可知本文算法处理后的切片数据分布比较均匀,可更为有效的用于曲线、曲面拟合.

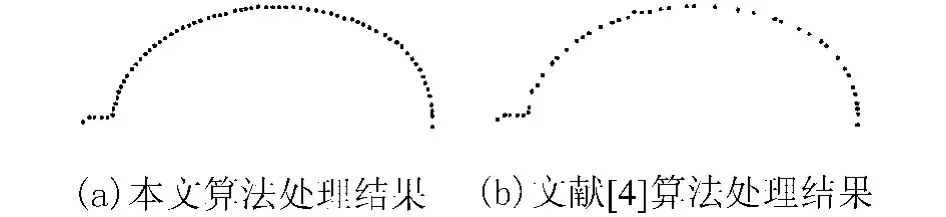
图8 两种算法切片数据处理效果Fig.8 Slice data processing of two algorithms

表1 本文算法切片数据误差分析计算结果Table 1 Error analysis of slicing data of this article

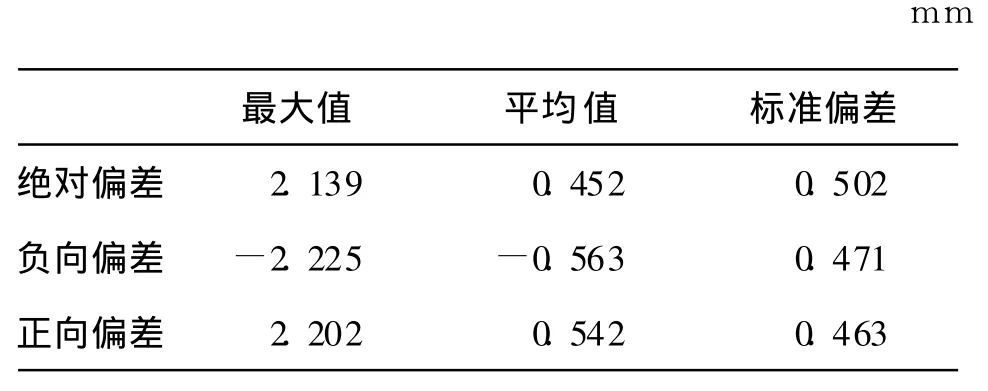
表2 文献[4]算法切片数据误差分析计算结果Table 2 Error analysis of slicing data of article 4

采用本文算法对图6(c)所示点云模型进行切片处理,切片位置分布如图9(a)所示,对切片数据进行精简与排序,得到的数据点序列如图9(b)所示,采用最小二乘法拟合为 B样条曲线,效果如图9(c)所示.由图可以看出,本文算法可有效处理复杂型面的散乱点云数据,处理后的数据可以有效表达模型型面特征.文献[4]以切片数据在直线上投影点的坐标值进行排序,不能有效处理此类多轮廓切片数据.

图9 本文算法切片数据处理效果Fig.9 Slice data processing of this article

5 结论

本文算法和相关算法相比具有以下特点：

1)采用 R*S树建立散乱点云动态索引,基于该结构快速获取切片数据,有效提高了切片数据获取效率;

2)通过极角区域划分获取区域形心点,并以形心点作为切片数据特征点,有效滤除了大量冗余数据,提高了切片数据精度;

3)基于距离阈值对不同轮廓切片数据进行分离,可有效处理各种多轮廓切片数据点云,数据适应性强;

4)在进行数据精简的同时,完成了数据点之间的排序,建立了数据之间的拓扑邻近关系,为参数曲线、曲面重构奠定重要基础.

[1]刘云峰,柯映林.反求工程中的混合切片技术[J].计算机辅助设计与图形学学报,2003,15(3)：741-745.LIU Yunfeng,KE Yingli.Hybrid slicing technology in reverse engineering[J].Journal of Computer Aided Design＆Computer Graphics,2003,15(3)：741-745.

[2]柯映林,王青.反求工程中点云切片算法研究[J].计算机辅助设计与图形学学报,2005,17(8)：1798-1802.KE Yinglin,WANG Qing.Research on point cloud slicing technique in reverse engineering[J].Journal of Computer Aided Design＆ Computer Graphics,2005,17(8)：1798-1802.

[3]盖绍彦,达飞鹏,雷明涛,等.三维重构中的杂乱点云排序问题研究[J].计算机与现代化,2003,98(10)：33-35.GAIShaoyan,DA Feipeng,LEIMingtao,et al.Research on sortingmethod of 3-D reconstruction of unorganized point-clouds[J].Computer and Modernization,2003,98(10)：33-35.

[4]龚友平,陈国金,陈立平.基于切片方法的截面数据处理[J].计算机辅助设计与图形学学报,2008,20(3)：321-325.GONG Youping,CHEN Guojin,CHEN Liping.Point data processing based on slicing method[J].Journal of Computer-Aided Design＆Computer Graphics,2008,20(3)：321-325.

[5]龚友平,金涛,童水光.截面切片数据的自动细化算法[J].浙江大学学报(工学版),2008,42(2)：337-340.GONG Youping,JIN Tao,TONG Shuiguang.Auto-thinning method for slice pointdata[J].Journal of Zhejiang University(Engineering Science),2008,42(2)：337-340.

[6]孙殿柱,刘健,李延瑞,等.三角网格曲面模型动态空间索引结构研究[J].中国机械工程,2009,23(13)：1542-1545.SUN Dianzhu,LIU Jian,LI Yanrui,et al.Research on dynamic spatial indexing structure of triangu lar mesh surface model[J].Chinese Journal of Mechanical Engineering,2009,23(13)：1542-1545.

[7]孙殿柱,范志先,李延瑞,等.散乱数据点云型面特征分析算法的研究与应用[J].机械工程学报,2007,43(6)：133-136.SUN Dianzhu,FAN Zhixian,LIYanrui,et al.Research and application of surface feature analysis for scatter data points[J].Chinese Journal of Mechanical Engineering,2007,43(6)：133-136.

[8]ZHU Qing,GONG Jun,ZHANG Yeting.An efficient 3-D R-tree spatial indexmethod for virtual geographic environments[J].ISPRS Journal of Photogrammetry and Remote Sensing,2007,62(3)：217-224.

[9]刘云峰,柯映林.反求工程中切片数据处理及断面特征曲线全局优化技术[J].中国机械工程,2006,42(3)：124-129.LIUYunfeng,KEYinglin.Slicing data processingand global optimization of feature curve in reverseengineering[J].Chinese Journal of Mechanical Engineering,2006,42(3)：124-129.