构架式可展开天线工作表面母线拟合方法

田大可，刘荣强，邓宗全，郭宏伟

(哈尔滨工业大学 机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150001)

可展开卫星天线是进行移动通信、深空探测和射电天文等空间科学任务必备的物理手段［1-2］.随着人们对信息多样化、复杂化的需求变得越来越迫切，可展开卫星天线正向着大型化、高精度化、轻量化方向发展，并且已经成为空间可展开结构中最活跃的一个分支.

按照天线工作表面的组成介质可将可展开卫星天线分为3类:固体反射面可展开天线、充气式反射面可展开天线、网面可展开天线［3］.其中，网面可展开天线由于其展开精度高、可实现较大的展开口径、技术相对成熟等优点正成为研究的热点.由六棱柱单元组成的构架式可展开天线除具有网面可展开天线共有的优点，还具有很高的灵活性，天线采用模块化思想设计，杆件类型大大减少，通过改变模块的尺寸或数量可以适应通信中对口径大小的要求，结构拓扑容易.并且由于天线由若干个相同的模块组成，可以在完成每个模块的测试后再进行总的装配.因此，大大降低了安装和调试的难度，缩短了安装时间，加工成本也大大降低［4］.

2006年底，日本国家空间发展局(NASDA)发射的工程试验卫星 ETS-Ⅷ上携带了2架19 m×17 m的构架式可展开天线，该天线能够与手机大小的地面移动终端进行卫星通信.构架式天线由若干个相同的模块组成.每个模块包括背部支撑桁架(背架)和金属反射网2个部分［5］.由于反射器表面必须是抛物面形状，相同的背架组成一个球面，因而两者之间存在形状的差异.目前的文献一般只指出解决此问题需要通过拟合方法，并没有给出其采用的方法和分析过程［6-8］.本文根据构架式可展开天线的特点，基于微分几何及最小二乘法，提出一种工作表面母线的拟合方法.

1 模块的结构与球面天线背架

1.1 模块的结构及其展开原理

构架式可展开天线模块的结构如图1所示，金属反射网是天线的工作部分，它下面的张紧索网将金属反射网张紧成工作所需的状态.金属反射网的形面精度的高低直接影响天线工作的好坏.背架是模块的骨架，背架的形状类似于一个截顶的六棱锥，它可以提供高的刚度，展开呈六棱柱状态，每个模块的背架由从中心杆发散出的6个相同的基本单元组成，具体如图2.

背架的展开原理与伞的张开原理类似［1］.背架由铰链、弹簧、电机和各种杆件组成.伸展力由位于每个模块中心杆上的弹簧来提供［7］，滑块与弹簧相连，能在中心杆上上下移动.展开的速度由电机释放绳索来控制.模块在收拢状态时，弹簧呈完全伸展状态，它将滑块推至顶端，同时滑块带动斜腹杆，使杆件向中心杆聚拢，实现收拢.当天线展开时，电机将与滑块相连的绳索拉紧，滑块移动到下端，天线完成展开.

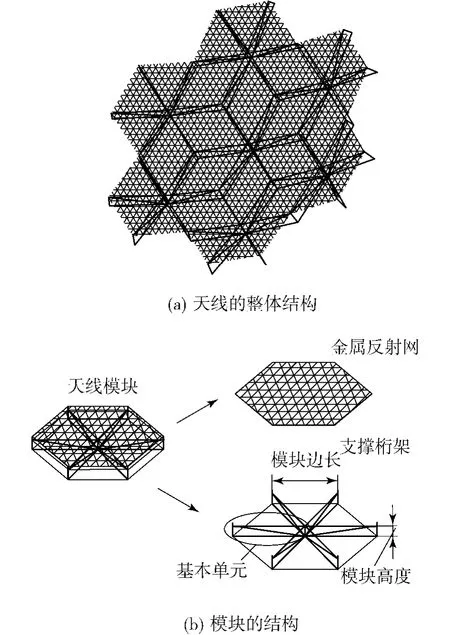
图1 天线的整体与局部结构Fig.1 The whole and part structure of antenna

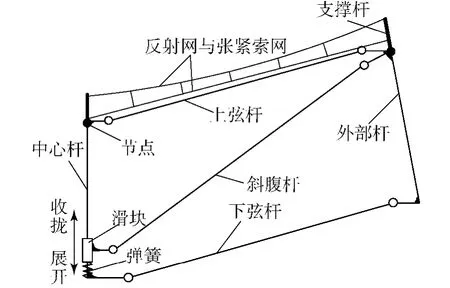
图2 基本单元的结构组成Fig.2 Structure composition of basic frame

1.2 构架式可展开天线的类型

卫星天线大多属于抛物面型天线，按工作表面被截区域不同，抛物面天线分为正馈型和偏馈型［9］.旋转抛物面被与其同轴的圆柱面所截而得到的那部分曲面是正馈抛物面天线;旋转抛物面被与其旋转轴平行但不同轴的圆柱面所截得的那部分曲面是偏馈型天线，如图3所示.由于偏馈天线的工作表面没有被馈源遮挡，在天线口径、制造精度、工作频率相同的前提下，偏馈天线的效率要优于正馈天线.正是由于偏馈天线的这一优点，构架式等很多星载天线都采用这种类型.

图3 抛物面天线类型Fig.3 Type of parabolic antenna

1.3 可展开球面天线背架与工作表面关系

背架位于金属反射网的背部，是金属反射网重要的支撑结构.图4为构架式可展开天线的剖面示意图.由于构架式天线采用模块化思想，各模块具有几乎相同的结构参数，因此背架与支撑杆连接的点位于同一个球面上.而作为天线工作表面的金属反射网必须是抛物面形状，这就导致球面背架的节点与工作表面存在误差，两者的差异通过支撑杆来调节，误差越大，需要的支撑杆越长.

考虑到天线整体结构的稳定性，支撑杆不易过长，根据文献［6，10］，模块边长、模块高度、支撑杆长度的比值为20∶5∶1.因此需要保证上弦杆上的节点所在的球面尽可能与天线工作表面相接近.这就需要寻找一种合适的拟合方法来缩小两者的差异，并且保证2个曲面间最大的误差小于支撑杆的长度.在对工作表面进行拟合时，首先要求出工作表面的方程，再通过拟合的方法，求出背架节点所在球面的球心坐标及半径.这些数据可为天线背架的结构设计提供理论基础.

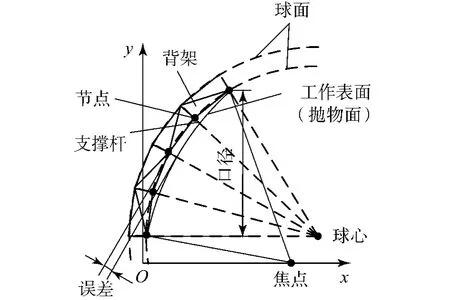
图4 背架与工作表面关系Fig.4 Relationshipbetween truss structure and working surface

2 天线工作表面的拟合方法

2.1 母抛物面母线方程的确定

天线工作表面为旋转抛物面，天线具有对称性，可以将问题简化为对抛物线的圆弧曲线拟合.由于工作表面是从母抛物面上切割的一部分，因此需先求出母抛物面的母线方程.如图5所示为母抛物面母线为工作表面母线.母抛物面母线的焦距与天线的有效口径的比值通常取f/D＞0.25，在这种情况下馈源位于口径面外侧，照射更加均匀.根据文献［7，11-12］，构架式可展开天线通常取f/D=0.8.

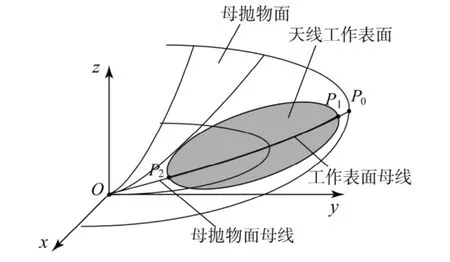
图5 偏馈天线示意图Fig.5 Schematic diagramof offset antenna

天线工作表面是一个空间曲面，可以认为它是一个由以包络矩形［13］的长边为母线绕旋转轴旋转得到的曲面，同时母线应满足抛物线方程.即存在一个由二维平面到三维曲面的变化，反之亦成立.构架式可展开天线组成模块的数量通常为3、7、14等［1］.以7个模块组成的构架式天线为例，如图6所示.

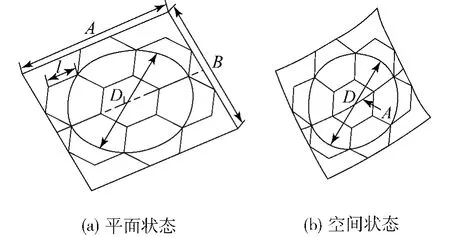
图6 天线平面与空间状态Fig.6 Plane state and space state of antenna

图6中，A和B分别为包络矩形的长边和短边，模块的边长为l，D1表示天线展成平面时的有效口径，可见天线绕旋转轴旋转后的尺寸比平面状态时要小，根据文献［4，12］，取天线有效口径 D=(0.87 ～0.97)D1.

由于天线以长边作为母线进行旋转，因此，只要保证对长边的拟合精度即可保证对天线的拟合精度.图7给出了3种组合的平面矩形包络图.

图7 不同数量模块的矩形包络图Fig.7 Rectangular envelope diagramof different amount ofmodules

根据三角函数，可求得3种模块组合时包络矩形的长边、短边及平面时的有效口径，如表1.

表1 包络矩形及平面时有效口径参数Table 1 Parameters of enclosure rectangle and effective aperture in plane state

母抛物面母线方程的求解过程如图8所示，其方程可表示为

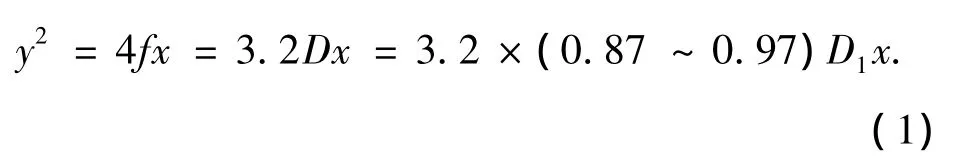
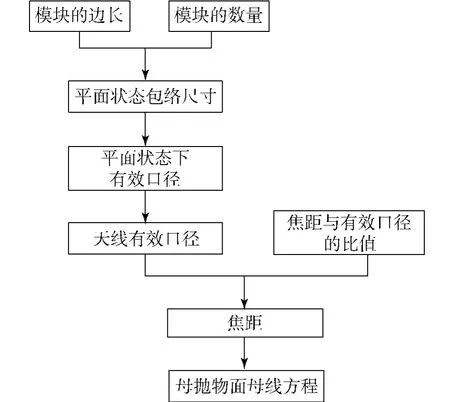
图8 母抛物面母线方程求解框图Fig.8 Solving steps ofmother paraboloid＇s generatrix equation

2.2 工作表面母线端点的确定

在母抛物面母线上取弧长为A的一段曲线，曲线的2个端点分别为P1和P2，假定天线的偏距为y0，则工作表面母线起点P2的坐标(x0，y0)为已知，因此只要求得终点P1的坐标(x1，y1)即可确定工作表面的母线方程，如图9所示.

由y2=4fx可知:

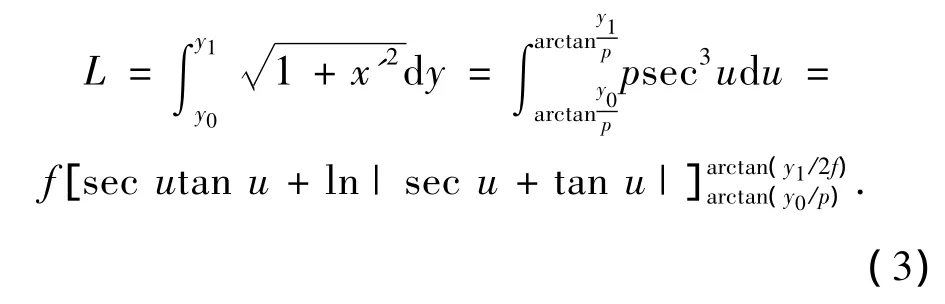
由式(3)即可求出另一个端点(x1，y1).天线的物理口径为

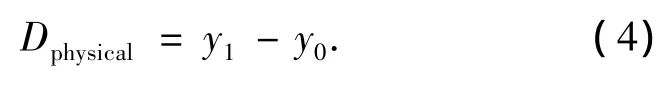
天线的利用率为

图9 工作表面母线参数Fig.9 Parameters ofworking surface generatrix

2.3 天线抛物线的拟合方法

圆弧拟合的一般方法有三点共圆法、双圆弧法等.三点共圆法是圆弧拟合最初始的方法，简单而快捷，但曲线上3个节点位置的选取对拟合精度的影响很大，由于拟合出的圆弧通过给定点，在未给定点处误差较大，实际上应用很少.双圆弧法虽然精度较高，但计算参数多，计算量大，拟合效率低，实际中也很少应用［14-15］.利用最小二乘法对天线抛物线进行拟合，拟合的曲线不需要通过所有的离散点，它能够很好地反应离散点的变化趋势，并且可以保证拟合误差的平方和达到最小.同时，拟合出的曲线在抛物线的后部，符合构架式天线对背架位置的要求.因而，本文采用最小二乘法对天线抛物线进行拟合.

在进行圆弧拟合时，最终要得到的是拟合圆弧的圆心坐标、圆弧半径以及拟合误差.如图10所示，设待拟合抛物线方程为y2=4fx，x0≤x≤x1，沿x轴方向，将该抛物线离散成步长相等的若干个离散点，设任意离散点坐标为(xi，yi)，i=1，2，…，n.拟合圆的标准方程为

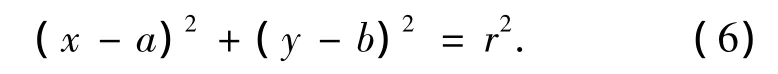
式中:(a，b)为圆心坐标，r为圆弧半径.

设c=a2+b2-r2，将式(6)展开并整理得

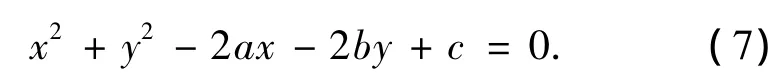
抛物线上某点到拟合圆弧中心的距离ri与拟合圆弧半径r之差即为拟合误差，则离散点i对最小二乘圆弧的误差为

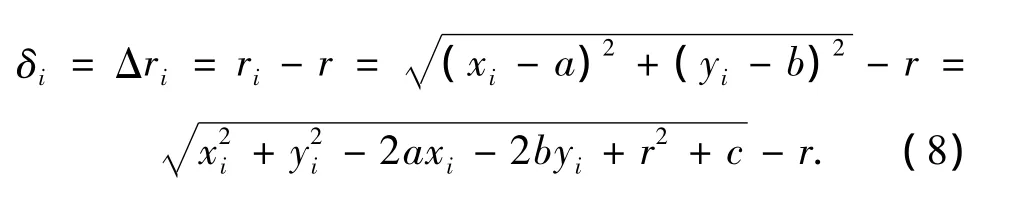
图10 抛物线的圆弧拟合Fig.10 Parabolic fitting with arc

根据最小二乘法的计算原则，使拟合误差的平方和为最小，由求多元函数极值的必要条件有

由此建立的是非线性方程组，直接求解比较困难.经过分析，ri和 r很接近［15-16］，所以 r2i-r2=(ri+r)(ri-r)≈2rδi，可以看出径向平方差(r2i-r2)与δi次数相同，只是相差一个系数，可以认为两者相等价，以(r2i-r2)代替δi可以解决上述问题，令

同理，再对 a、b、c求偏导并整理得

通过式(11)即可求出a、b、c这3个参数的值，这样就可以求得拟合圆弧的圆心坐标及圆弧半径.

2.4 抛物线拟合的误差修正

由于最后拟合出的圆弧与原抛物线之间的差异是由支撑杆来调节的，因此需要将得到的离散点的拟合误差与许用的误差［δ］即支撑杆的长度进行比较.由于支撑桁架在天线工作表面的背部，因此需要重点考虑 δi⊂(-δmax，0).如果|- δmax|≤［δ］，则拟合结果满足精度要求.否则，需要对拟合曲线进行修正.

图11 误差修正Fig.11 Error correction

如图11所示，在拟合曲线段内，计算所有点的误差，在误差最大点处，沿径向移动，满足:

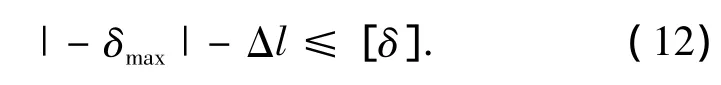
式中:-δmax表示抛物线背部的最大误差，Δl表示移动距离.

从式(12)及图11可以看出移动距离越大，需要的支撑杆长度越短，结构越稳定，但球面背架位于工作表面后部的部分将减少，有效口径会随之减小，天线的工作效率会降低，所以保证在误差最大点处移动后的距离等于支撑杆长度即可.

移动的方向为

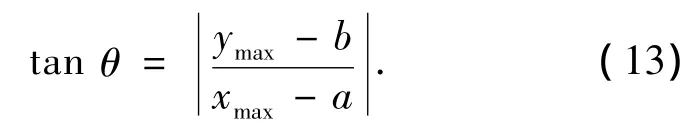
式中:θ为径向与x轴的夹角，(xmax，ymax)为误差最大点的坐标.

修正后，拟合圆弧的圆心坐标为(a+Δl cosθ，b-Δl sin θ)，圆弧的半径不变，仍为 r.

3 拟合方法算例

本文用3种不同数量的模块组合对具有相同口径要求的天线进行了工作表面拟合.天线的参数见表2.

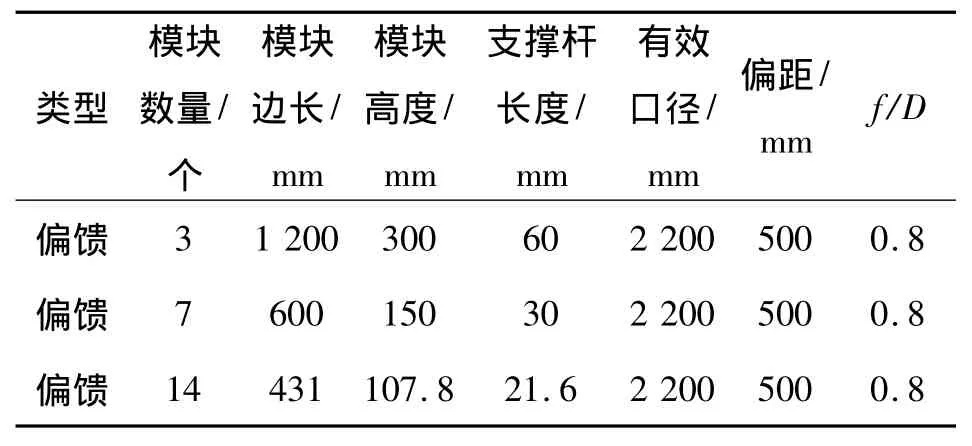
表2 天线参数Table 2 Parameters of antenna

根据上述方法，计算得到包络矩形、母抛物面母线方程、起点、终点、拟合圆弧圆心、半径等参数，见表3.并得到拟合曲线，如图12所示.

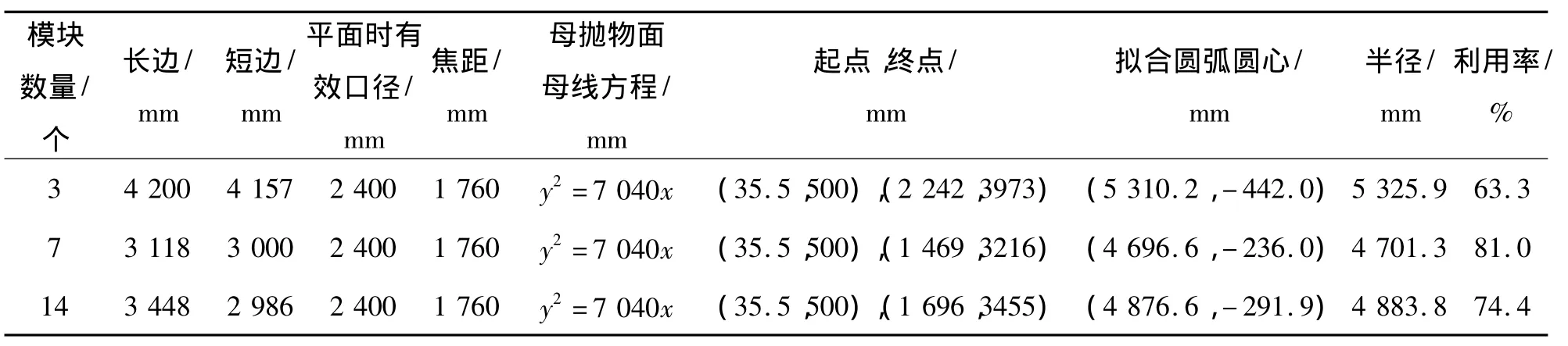
表3 拟合后得到的天线参数Table 3 Antenna parameters after fitting

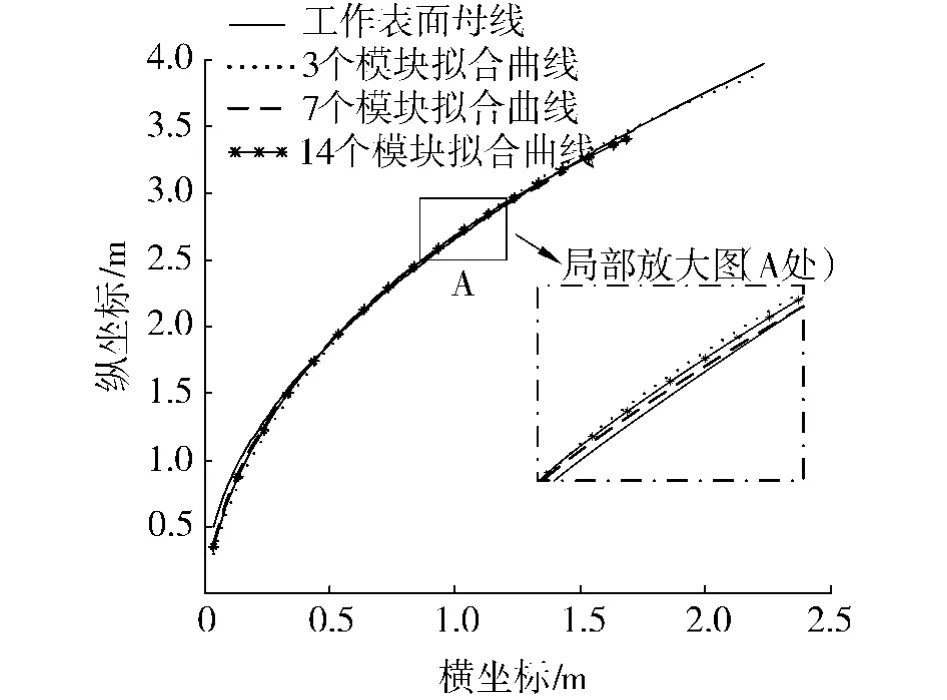
图12 曲线拟合图Fig.12 Curve fitting

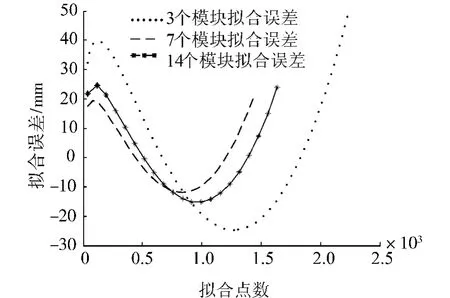
图13 拟合误差曲线Fig.13 Curves of fitting error

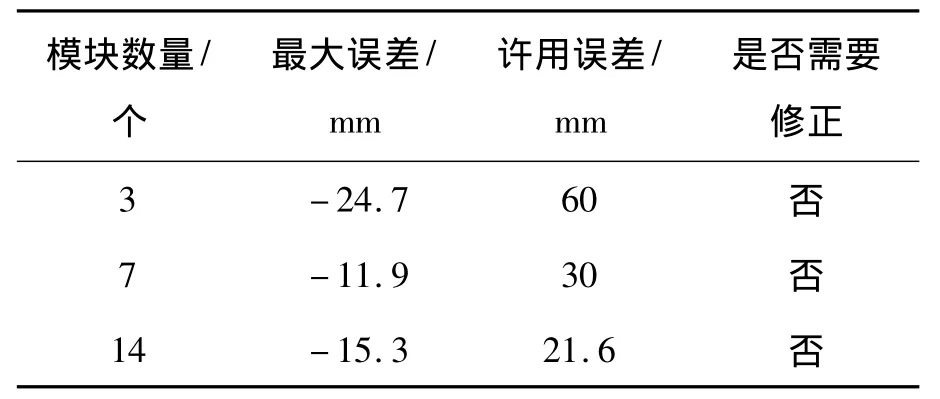
表4 拟合误差对比Table 4 Comparison of fitting error

从表3及图12可以看出:3种拟合的曲线均能够反映母线的变化趋势.在各自所拟合的母线段内圆弧的中部均在母线的左侧即背架在工作表面的后部，符合设计要求.设计一个相同口径的天线时，7个模块组成的天线所需的包络矩形的面积最小，并且其利用率最高(81.0%)，其次为 14个模块(74.4%)，3 个模块的利用率最低(63.3%).分析误差时，首先需要研究在母线中部误差最大点的误差值.得到3种组合的最大误差，见表4，它们均小于各自的许用误差，不需要修正.其次，考虑整个拟合段内各点的误差值，如图13所示.

对图13中的3条曲线进行误差分析，得到它们的均方根值分别为22.9、11.1、14.2 mm.可见，7 个模块的均方根值最小，说明它的误差曲线离散性最小，曲线的拟合精度最高.

4 结论

本文针对构架式可展开天线抛物面形工作表面与球形支撑背架形状差异的问题进行了研究，根据背架的结构特点及展开原理，分析了问题产生的原因，提出了一种工作表面母线的拟合方法，并通过算例对该方法进行了验证，得到如下结论:

1)进行误差修正时，沿最大误差点处法线方向移动的距离越大，需要的支撑杆长度越短，结构越稳定，但天线有效口径越小，因此，移动距离不宜过大，保证修正后的距离等于支撑杆长度即可.

2)对同一口径的天线进行设计时，由7个模块组成的天线所需包络矩形的长边最短，天线的利用率最高，拟合误差最小.

3)算例表明3种组合的最大的拟合误差均小于各自的许用误差，不需要进行修正.本文方法能够较好地实现对构架式可展开天线工作表面母线的拟合，可为构架式可展开天线背架的结构设计提供理论基础.

［1］MIYASAKA A，HOMMATM，TSUJIGATA A.Design and ground verification of large deployable reflector［C］//42nd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference and Exhibit.Seattle，USA，2001.

［2］MEGURO A，HARADA S，WATANABEM.Key technologies for high-accuracy large mesh antenna reflectors［J］.Acta Astronautica，2003，53(11):899-908.

［3］刘世海.可展开卫星天线展开结构可视化辅助概念设计软件原型［D］.西安:西安电子科技大学，2005:6-21.LIU Shihai.Software prototype of visualization aided model for structure of deployable satellite reflector antenna conceptdesign［D］.Xi＇an:Xidian University，2005:6-21.

［4］YAMADA K，TSUTSUMIY J，YOSHIHARA M，et al.Integration and testing of large deployable reflector on ETSVIII［C］//21st International Communications Satellite Systems Conference and Exhibit.Yokohama，Japan，2003.

［5］MITSUGI J，ANDO K，SENBOKUYA Y，et al.Deployment analysis of large space antenna using flexible multibody dynamics simulation［J］.Acta Astronautica，2000，47(1):19-26.

［6］MEGURO A，ISHIKAWA H，TSUJIHATA A.Study on ground verification for large deployable modular structures［J］.Journal of Spacecraft and Rockets，2006，43(4):780-787.

［7］UCHIMARU K，NAKAMURA K，TSUJIHATA A，et al.Large deployable reflector on ETS-VIII.II［C］//18th AIAA International Communications Satellite Systems Conference and Exhibit.Oakland，USA，2000.

［8］NATORImC，HIRABAYASHIH，OKUIZUMIN，etal.A structure concept of high precision mesh antenna for space VLBI observation［C］//43rd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference.Denver，USA，2002.

［9］段宝岩.柔性天线结构分析、优化与精密控制［M］.北京:科学出版社，2005:1-13.

［10］ANDO K，MITSUGI J，SENBOKUYA Y.Analyses of cable-membrane structure combined with deployable truss［J］.Computers ＆ Structures，2000，74(1):21-39.

［11］NAKAMURA K，TSUTSUMI Y，UCHIMARU K，et al.Large deployable reflector on ETS-VIII I［C］//AIAA 1998，1998-1229.

［12］MEGURO A，TSUJIHATA A，HAMAMOTO N，et al.Technology status of the13maperture deploymentantenna reflectors for engineering test satellite VIII［J］.Acta Astronautica，2000，47(2-9):147-152.

［13］李瑰贤.空间几何建模及工程应用［M］.北京:高等教育出版社，2007:128-145.

［14］姚必强，姚进.数控加工曲线的等弧长圆弧拟合方法［J］.四川大学学报(工程科学版)，2008，40(1):171-174.YAO Biqiang，YAO Jin.Themethod of curve fitting with equal length arc used for NC processing［J］.Journal of Sichuan University(Engineering Science Edition)，2008，40(1):171-174.

［15］乐英，韩庆瑶，王璋奇.数控加工中非圆曲线的最小二乘圆弧逼近［J］.华北电力大学学报，2006，33(6):102-104.YUE Ying，HAN Qingyao，WANG Zhangqi.Leastsquares approximation for non-circular curve in NC machining［J］.Journal of North China Electric Power University，2006，33(6):102-104.

［16］沈世德，徐辛伯.最小二乘圆弧法在圆图象分析中的应用［J］.机械设计与制造，1999(5):46-47.SHEN Shide，XU Xinbo.The application of themethod of least square arc to circular figure analysis［J］.Machinery Design＆ Manufacture，1999(5):46-47.