基于直觉模糊集和 POWA算子的目标类型识别方法

徐永杰, 李登峰, 张 娜, 伍之前

(1.海军大连舰艇学院,辽宁 大连 116018; 2.大连市政府发展研究中心,辽宁 大连 116012)

0 引言

从数据融合角度划分,目标类型识别分为信号级融合、特征级融合和决策级融合 3类,目前的相关文献多从特征级融合角度研究[1-3]。编队级目标类型识别属于决策级融合,其信息源包括上级指挥所、友邻编队、下属作战平台,信息的内容是目标类型的情报。同时,信息源因为指挥层级的特性而具有不同的优先等级差异,情报内容因为传感器可靠性、战场环境复杂性等原因,具有明显的不确定性。

针对具有优先级的多准则决策问题,美国学者Yager在 OWA算子[4]基础上提出了可以集结模糊信息的优先有序加权平均(Prioritized OWA,简称为POWA)算子[5];在处理模糊性和不确定性等方面,Atanassov[6]提出的直觉模糊集比 Zadeh的模糊集[7]更具灵活性和实用性。为此,可以应用直觉模糊集描述各个信息源提供的目标情报信息,用准则优先级描述信息源的指挥层级特点,编队级目标类型识别问题可以归结为一类具有优先级的直觉模糊多准则决策问题。本文把 POWA算子扩展到直觉模糊集,应用扩展的 POWA算子研究舰艇编队目标类型融合识别方法。

1 直觉模糊集上的扩展 POWA算子

1.1 预备知识

设 X是一个给定论域,则 X上的一个直觉模糊集A为:A={＜x,μA(x),v(x)＞|x∈ X},其中 μA(x)∶X→[0,1]和 vA(x)∶X→[0,1]分别代表 A的隶属度函数μA(x)和非隶属度函数 vA(x),且对于 A上的任意 x∈X,都有 0≤μA(x)+vA(x)≤1成立,而且称 πA(x)=1-μA(x)-vA(x)为 x对 A的犹豫度 。

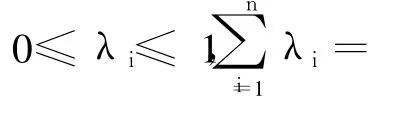
定义 1设 ai∈[0,1],i=1,2,…,n为一组实数,Pi为相应的优先级别,且具有优先关系 p:P1＞P2＞…＞Pn;若 fp∶[0,1]n→[0,1],使得 :

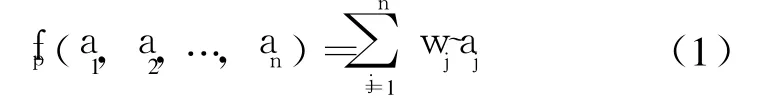
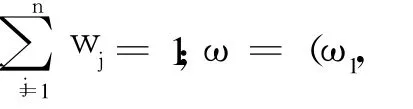
POWA算子关联权重的计算思路是:首先通过优先关系得到基于优先级的属性权重,其次是以无优先关系下的 OWA算子权重作为初始权重,然后利用特别构造的基本单位区间单调(Basic Unit-interval Monotonic,BUM)函数和优先级属性权重获得 POWA算子关联权重向量。

1.2 直觉模糊扩展算子

为方便起见,称 a=＜μa,va＞为直觉模糊数,μa,va∈[0,1],μa+va≤1,且称 Θ为全体直觉模糊数的集合。

定义 2设 ai=＜μ(ai),v(ai)＞,i=1,2,…,n为一组直觉模糊数,Pi为相应的优先级别,且具有线性优先关系 p:P1＞P2＞… ＞Pn。若 F(ω,p)∶Θn→Θ,使得:

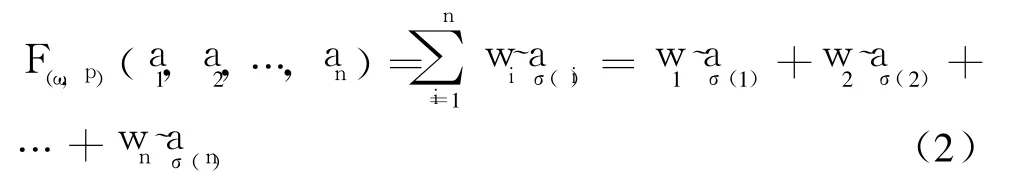
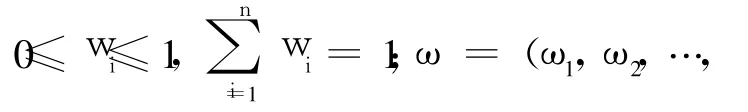
Yager教授用准则值计算优先级权重,在直觉模糊条件下权重计算方法需要改进,这里考虑采用直觉模糊数的得分值[8]来计算。下面给出 IFPOWA算子关联权重向量计算步骤。

1)令 Vi表示直觉模糊信息的大小,其中:

2)因为 S(ai)∈ [-1,1],所以 (Vi+1)∈ [0,1]。

令 Ti表示各个优先级别直觉模糊信息相对重要程度的度量,其中:

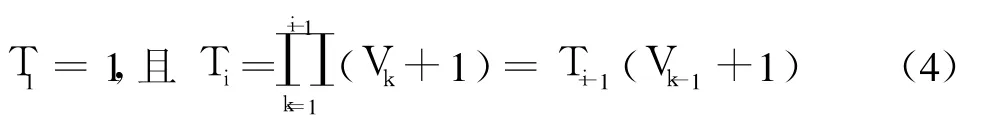
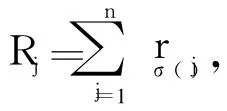
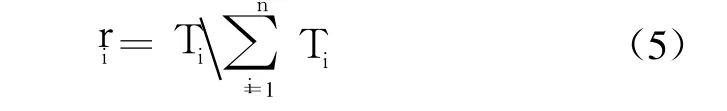
4)选择 BUM方程为

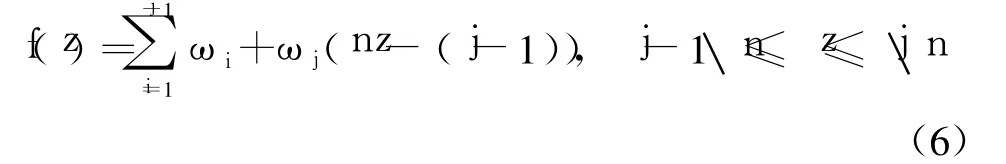
5)令权重向量为 w=(w1,w2,…,wn)T,则:

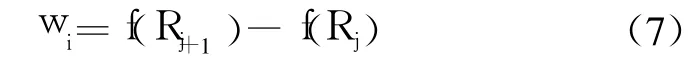
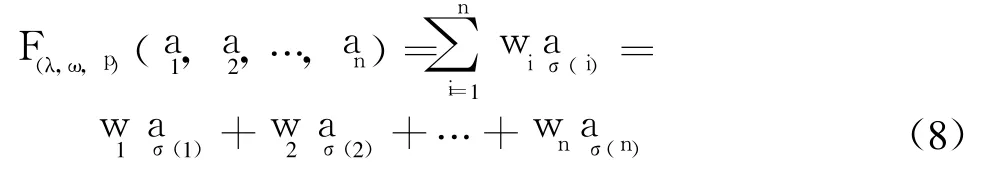
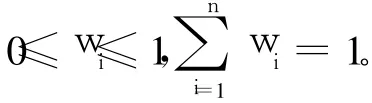
IFHPOWA算子融合了基于优先级的权重、基于确定性的权重和基于 OWA算子的权重,其关联权重向量计算方法只需在 IFPOWA算子关联权重计算方法中的 “ai”替换为 “naiλi”,将 “~aσ(i)”替换为 “aδ(i)”即可 。

2 舰艇编队空中目标类型融合识别方法

水面舰艇编队的目标类型融合识别功能由指挥控制信息中心完成,其信息源有上级的敌情通报,友邻编队的共享信息,下属舰艇的初步判断等。其融合功能如图 1所示。

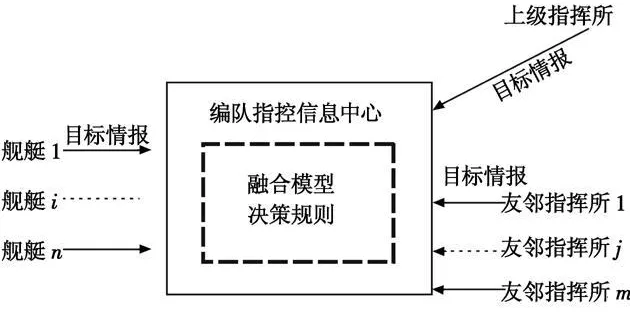
图1 编队指挥信息中心融合示意图Fig.1 C2 information center fusion of ship formation

各个情报信息的来源因为指挥层次的区别而具有优先等级,各种情报信息由于传感器可靠性、战场环境复杂性以及对作战目标知识和感知经验缺乏等原因,具有明显的不确定性,可以应用直觉模糊集描述各个信息源提供的目标类型信息,用准则优先级描述信息源的指挥层级特点对编队情报融合目标类型识别问题建模。

舰艇编队目标类型融合识别问题数学描述:设 P1表示上级指挥所;P2表示友邻编队集合;P3表示下属舰艇集合。P1={S11},P2={S21,S22,…,S2n2},P3={S31,S32,…,S3n3},有 q=(1+n2+n3)个信息源,显然存在优先关系:P1＞P2＞P3。设目标类型划分为 T={T1,T2,T3,T4,T5}。令1,2,3;j=1,…,max{1,n2,n3}表示由 Sij判断目标 O是Tl类型的直觉模糊数,则 Sij的目标情报表示为一个直觉模糊集则直觉模糊识别决策矩阵,其中 :i=1,2,3;j=1,…,max{1,n2,n3}。

应用本文定义的扩展 POWA算子,建立舰艇编队空中目标类型融合识别方法如下所示。

步骤 1 应用 IFWA算子[9]集结同一优先级别中的直觉模糊信息。分别计算级别内各个信息源信息的直觉模糊熵 H(Aij),i=1,2,3;j=1,…,max(1,n2,n3),根据文献[10]的直觉模糊熵权计算方法得到相应集结权重

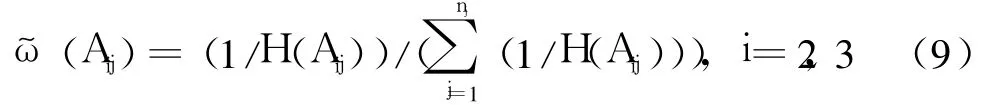
根据直觉模糊集运算法则和 IFWA算子,计算得到级别直觉模糊集 Ak,k=2,3为

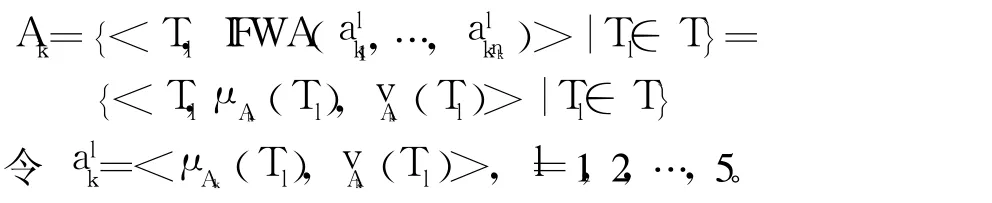
步骤 2 应用 IFHPOWA算子集结不同优先级别的直觉模糊信息。计算 3个优先级别信息源信息的直觉模糊熵 H(Ak),k=1,2,3,相应地确定性权重为

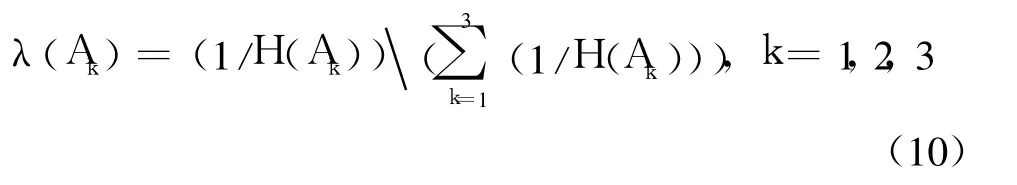
根据式(3)～式(7),得到 IFHPOWA算子关联权重向量 w=(w1,w2,w3)T,k=1,2,3,若为=1,2,3中第 k大的元素,则根据式(8),令:

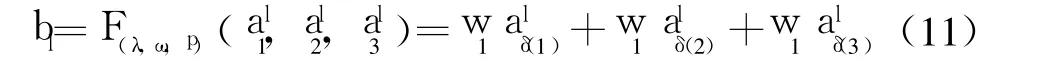
得分向量 b=(b1,b2,b3,b4,b5)T。

步骤 3 对各个类型的直觉模糊综合得分值进行比较排序和识别决策。应用得分函数和精确函数[11]对 bl大小进行比较,对目标类型归属进行排序并做出识别决策。

3 舰艇编队空中目标类型融合识别实例

编队指挥信息中心在 t0时刻收到来自上级指挥所情报:一批来袭目标 O很可能是 T2,也有可能是 T1,不太可能是 T3,绝不可能是 T4和 T5。用直觉模糊集表示为 A1={＜T1,0.6,0.3＞,＜T2,0.8,0.1＞,＜T3,0.1,0.7＞,＜T2,0,1＞,＜T5,0,1＞},t1时刻得到两个舰艇对目标 O的初步类型识别结果,t2时刻收到两个友邻编队对目标 O共享战场态势信息,用直觉模糊集对目标 O的类型进行描述,得到的初始直觉模糊识别矩阵为

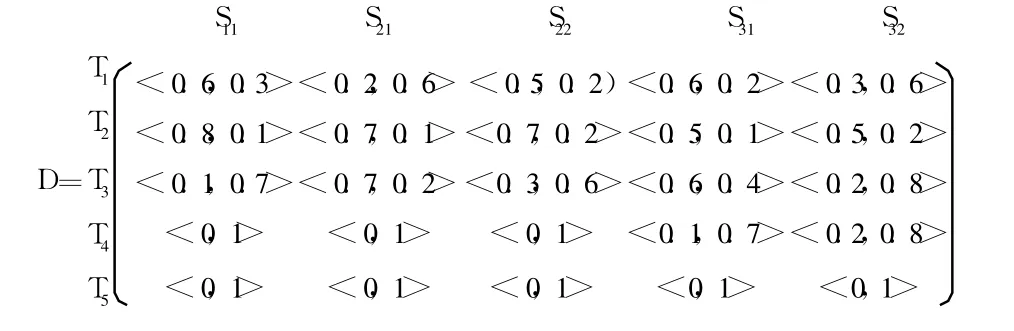
首先,应用文献[12]的直觉模糊熵函数,利用式(9),计算信息源直觉模糊熵向量为 H=(H(A11),H(A21),H(A22),H(A31),H(A32))T=(0.25,0.275,0.314,0.39,0.329)T,P2,P3级别内的直觉模糊熵权分别为21=0.53,22=0.47和31=0.46,32=0.54。

再应用 IFWA算子,对 P2,P3级别内的直觉模糊信息进行集结,进而得到 3个优先级别的目标类型识别矩阵:

利用式(10),得到 A1,A2,A3的直觉模糊熵和直觉模糊熵权分别为:H(A1)=0.25;H(A2)=0.28,H(A3)=0.496;λ=(λ1,λ2,λ3)T=(0.41,0.37,0.22)T。

下面,以目标类型 T1为例,应用 IFHPOWA算子计算其直觉模糊综合得分。

2)取初始权重向量 ω=(0.5,0.4,0.1)T,根据式(6),得到 BUM方程为

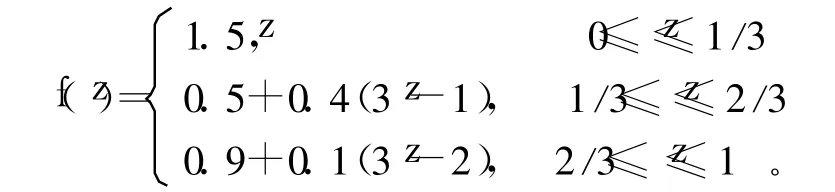
3)利用式(7)计算得到优先有序权重向量为:w=(w1,w2,w3)T=(0.58,0.345,0.075)T。

4)根据式(11),应用 IFHPOWA算子集成目标类型 T1的直觉模糊综合得分:

同理,可以计算其他目标类型的直觉模糊综合得分,得到直觉模糊识别得分向量为 b=(b1,b2,b3,b4,b5)T=(＜0.57,0.28＞,＜0.81,0.087＞,＜0.33,0.65＞,＜0,0.97＞,＜0,1＞)T。

5)根据得分函数比较可得出 b2＞b1＞b3＞b4＞b5,所以识别目标为 T2类型。

4 结论与展望

直觉模糊集上的扩展 POWA算子解决了具有优先级的直觉模糊信息集结问题,能够应用于直觉模糊条件下的多准则决策问题。应用直觉模糊集理论研究编队空中目标类型融合识别问题,结合直觉模糊熵权的思想和直觉模糊加权平均算子,应用直觉模糊优先有序加权平均算子建立的融合模型有效地处理了来自不同指挥层级的目标情报融合问题。下一步将研究简化直觉模糊优先有序加权平均算子的关联权重的计算方法和算子性质。

[1] 孙玉鹏,李延磊,孙暄.基于最大隶属度与证据理论的目标识别融合[J].电光与控制,2007,14(6):60-63.

[2] 史豪杰,邢清华,沈继承.基于支持向量机和无源特征的目标识别方法[J].电光与控制,2009,16(2):36-38.

[3] 刘海燕,陈琳,史志富.基于模糊贝叶斯网络目标多传感器融合识别[J].电光与控制,2009,16(3):37-41.

[4] YAGER R R.On ordered weighted averaging aggregation operators in multi-criteria decision making[J].IEEE Transactions on Systems,Man,and Cybernetics,1988,18:183-190.

[5] YAGERR R.Prioritized aggregation operators[J].International Journal of Approximate Reasoning,2008,48(1):263-274.

[6] ATANASSOV K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20:87-96.

[7] ZADEH L A.Fuzzy sets[J].Information and Control,1965(8):338-353.

[8] CHEN S M,TAN J M.Handling multicriteria fuzzy decision-making problems based on vague set theory[J].Fuzzy Sets and Systems,1994,67(2):163-172.

[9] 徐泽水.直觉模糊信息集成理论与应用[M].北京:科学出版社,2008.

[10] 徐永杰,李登峰,伍之前,等.基于直觉模糊熵和CC-OWA算子的雷达目标识别模型 [J].数学的实践与认识,2009,39(10):86-90.

[11] HONG D H,CHOI C H.Multicriteria fuzzy decisionmaking problems based on vague set theory[J].Fuzzy Sets and Systems,2000,114(1):103-113.

[12] VLACHOSIK,SERGIADISGD.Intuitionistic fuzzy information-applications topattern recognition[J].Pattern Recognition Letters,2007,28(2):197-206.