基于灰色组合模型的装备故障间隔时间预测研究

刘 熠, 周 林

(空军工程大学导弹学院,陕西 三原 713800)

0 引言

现代装备系统日趋复杂,使用过程中发生故障在所难免。如何利用好有限的数据样本,预测故障发生的时间,掌握维修保障的主动权,节约维修保障资源,对于充分发挥装备的使用效能,提高部队的战斗力水平,有着积极重要的意义。本文通过分析典型的故障规律,简化建模背景,建立灰色组合模型,比较模型间的预测效果,进而得出分阶段的灰色组合模型要优于整体和阶段上的单一灰色模型的结论。

1 建模背景的假定

建模的对象是装备发生的故障信息,因此有必要对故障阶段和属性进行简化,形成合理的建模背景。

1.1 装备故障阶段的简化

在使用过程中装备发生故障的规律极其复杂,一般的数学模型难以满足故障预测的精度。为简化建模背景,假定装备在全寿命范围内所发生的故障整体在时间轴上可以分成几个故障阶段且只存在线性、指数和随机 3种性质的故障,设所研究的装备发生故障的规律符合故障率随时间变化规律—“浴盆曲线”,如图1所示。

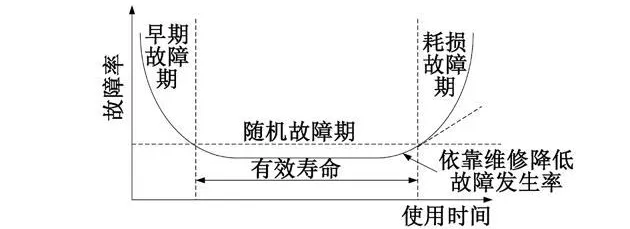
图 1 浴盆曲线图Fig.1 The bathtub curve of failure rate

由图 1可知,装备在全寿命过程中发生的故障分3个阶段:第 1阶段为早期故障期,因为设计、制造等原因造成故障率一般较高,但经运转、磨合,故障率逐渐下降并趋于稳定状态;第 2阶段为随机故障期,不易发生故障,故障率较低,并呈现随机波动性;第 3阶段为耗损故障期,因零件磨损,电气线路老化等因素,造成故障率逐渐回升,并且此过程的逆过程和早期故障期具有相似性[1]。

1.2 装备故障属性的简化

根据装备故障的浴盆曲线规律,在同一故障阶段对故障属性做一些简化假设,假设复杂故障可以看成是简单故障的线性组合,且组合后不影响原有故障的关键属性,将对应故障特点的模型进行适当的组合,形成组合预测法,往往得到更准确的信息。据相关统计,早期和耗损故障率有指数和线性共存的现象;而随机故障率,又具有随机波动性,分段建模是有必要的,故采取先分段后组合的方式对模型进行改进,可以提高预测精度[2-3]。以上故障简化的假定是建模的现实背景,后续建模过程都是在这一背景下进行的。

2 灰色预测及其组合模型

2.1 灰色预测 GM(1,1)模型

灰色系统理论是一种研究少数据、贫信息不确定性问题的新方法,以“部分信息明确,部分信息不明确”的“小样本”、“贫信息”不确定系统为研究对象[4]。GM(1,1)可用于时间序列的预测,其模型表述如下所述。

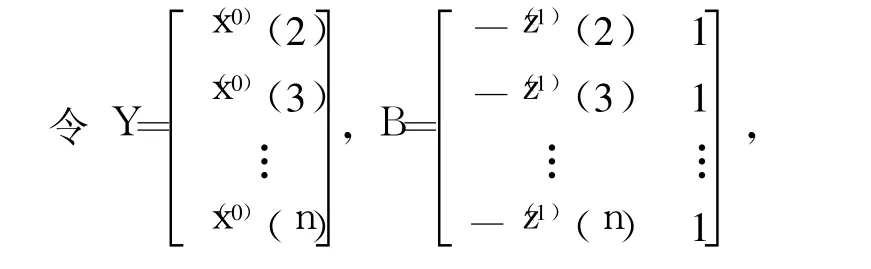
则 GM(1,1)模型为

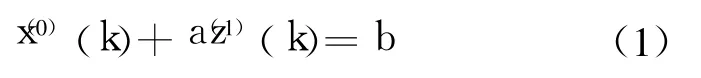
其中:a为发展系数,其大小和符号,反映了原始序列X(0)(k)和其 AGO序列 X(1)(k)的发展态势;b为灰作用量,不可以直接观测,需要通过计算得到。

GM(1,1)模型时间响应序列为

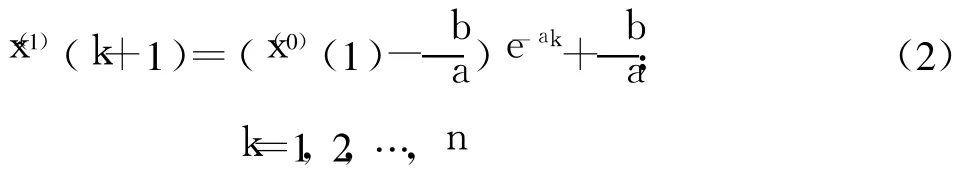
还原值为

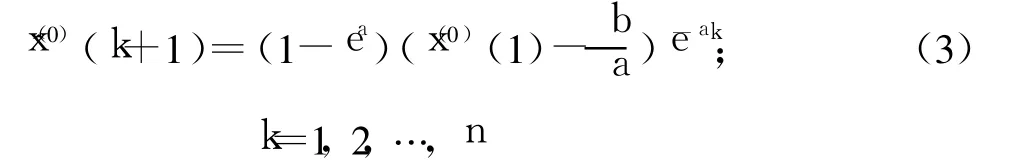
其中:a^=[a,b]T=(BTB)-1BTY。

2.2 灰色—线性回归组合模型

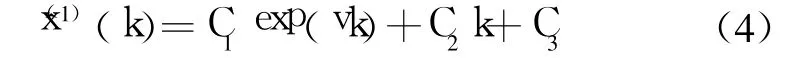
(参数 v,C1,C2,C3待求)

设有参数序列:z(k)=x^(1)(k+1)-x^(1)(k);k=1,2,…,n-1。

设ym(k)=z(k+m)-z(k),则。将 z(k)中的 X^(1)换成 X(1),得不同 m的 v的近似解 ~vm(k),则 ^v=令 L(k)=exp(^vk),则 x^(1)(k)可以改写成:

则C=(ATA)-1ATX(1)。

2.3 灰色 -马尔可夫组合模型

1)划分状态。

设原始序列:X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),按 GM(1,1)模型求出其预测值 Y^=(y^(1),y^(2),…,y^(n)),其中 y^(k)=x^(0)(k),k=1,2,…,n。

2)计算状态转移概率矩阵。

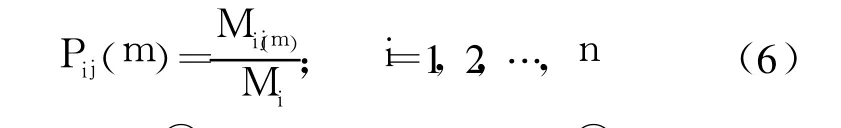
3)得出预测值。

由计算得知系统处于⊗k状态,则有:

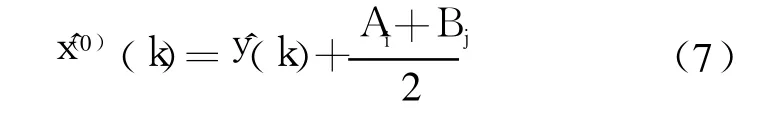
2.4 误差检验

残差为 ε(k)=x^(0)(k)-x(0)(k),相对误差为

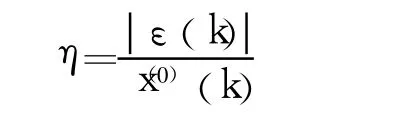
3 应用举例

以某型地空导弹的发射系统故障为例,因耗损故障期可以看成早期故障期的逆过程,故只截取早期和随机两段,故障间隔时间序列见表 1(单位:h)。

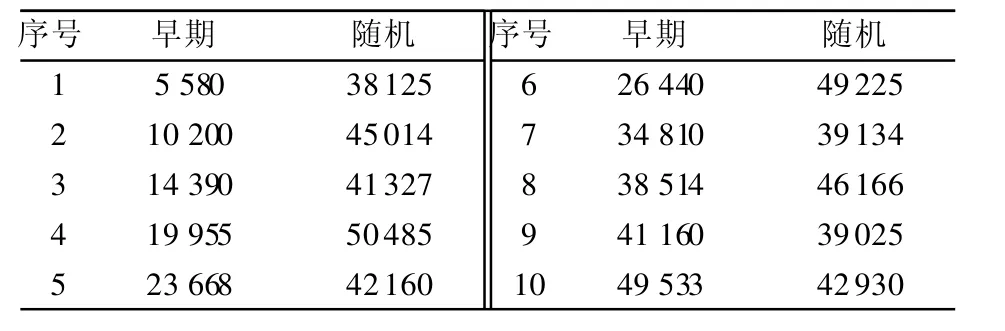
表 1 故障间隔时间Table 1 The time between failures

3.1 数据处理

取前 8个数据为原始数据序列,后 2个数据用来与模型产生的预测值进行效果比较。对早期原始数据序列分别采用 GM(1,1)模型和灰色 -线性回归组合模型进行预测,对随机原始数据序列分别采用 GM(1,1)模型和灰色 -马尔可夫组合模型进行模拟和预测,预测效果见表 2和表 3。

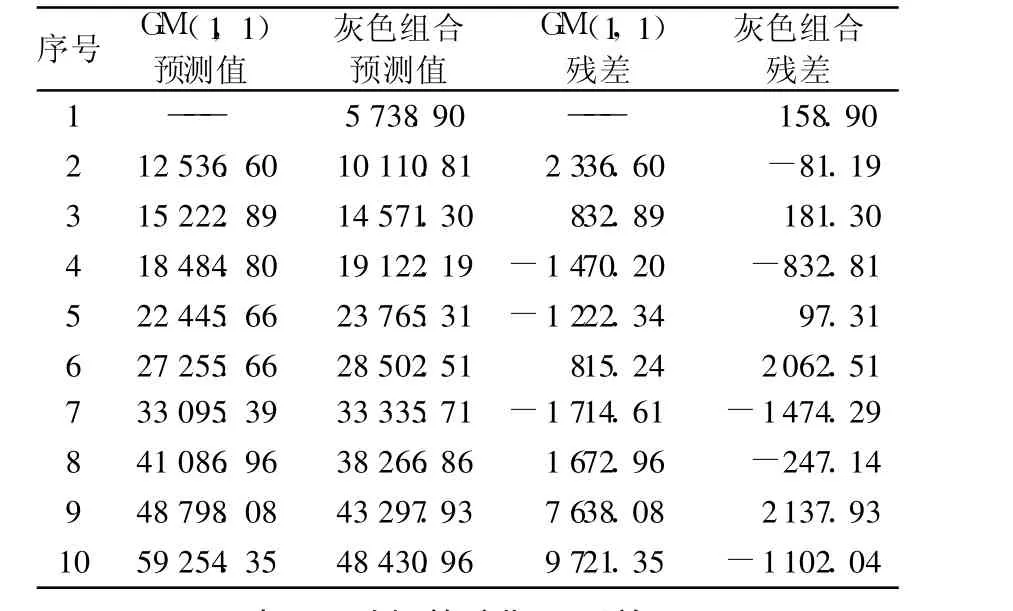
表 2 早期故障期预测效果Table 2 The effect on predictions in early fault period

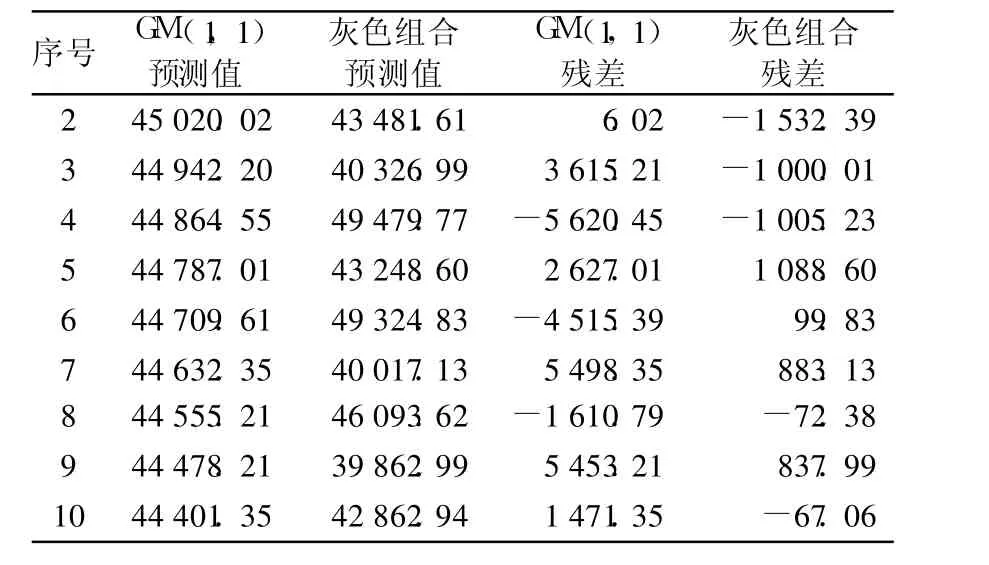
表 3 随机故障期预测效果Table 3 The effect on predictions in random fault period

3.2 模型比较

各模型预测值的相对误差和平均相对误差见表4。

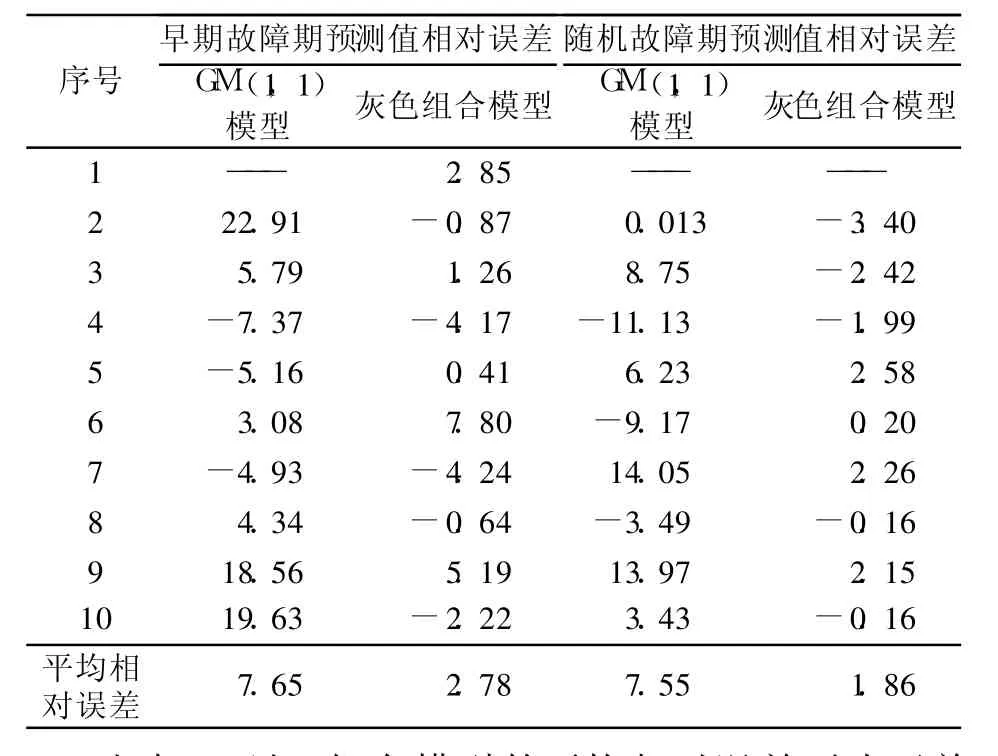
表 4 预测模型误差分析Table 4 The error analysis of prediction models

由表 4可知,组合模型的平均相对误差要小于单一的灰色预测模型,且在未来两步预测中效果相当明显,因此组合模型具有更好的预测能力。

4 结论

建立故障预测模型需考虑的因素众多,其中最重要的是简化并抽象出建模背景,并根据系统结构功能特点及产生的故障属性,分析判断系统所产生数据的主要性质和关键成分,合理选取数学模型。为克服单一模型的缺陷,可以分段选用相应的数学模型并进行优势重组,这样得出的预测结论才具备真实可信性。

[1] 李士军.机械维修技术[M].北京:人民邮电出版社,2007:77-79.

[2] 姜启源,谢金星,叶俊.数学模型[M].3版.北京:高等教育出版社,2003.

[3] 韩冬梅,牛文清,于长锐.组合预测建模中单项预测模型筛选研究[J].系统工程与电子技术,2009,31(6):1381-1385.

[4] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].3版.北京:科学出版社,2004.

[5] 蒋永仪.灰色马尔可夫预测模型[J].重庆建筑大学学报,1996(3):116-122.

[6] 章柏红,谢孔峰.灰色-马尔可夫链预测建模方法及其应用[J].海南师范大学学报,2008,21(4):469-477.