基于MATLAB的数控加工最短走刀路线研究

陈 玲

CHEN Ling

（昆明学院 自动控制与机械工程系，昆明 650118）

1 问题的提出

数控加工设备被广泛应用，相比普通机床设备其具有诸多优点，其中高效率是数控设备的重要优点之一。要充分发挥这一优点，需要工艺人员合理规划加工轨迹。

要选择最短的走刀路线，通常工艺人员可以直观的进行准确判断，但在特殊情况下，只有通过详细计算才能准确的分辨出最短路线所在。例如下图所示，在某零件的上表面需加工沿圆周均匀分布的两圈孔，刀具走怎样的路线是最短的呢？

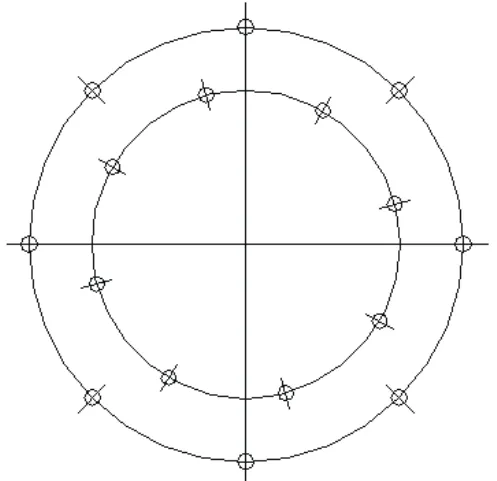
图1 零件上需加工孔的位置示意图

通常有两种做法：1）外圈加工完一个孔后，走斜线加工内圈和此孔距离最近的孔，再走斜线加工外圈相邻的孔，依次循环，直至加工完所有孔。走刀路线如图2a)所示。2）先沿外圈顺序加工完全部孔，再转到内圈依次加工各孔。如图2b)所示。

图2 走刀路线图

工艺人员容易认为方法一所走的加工路线最短，但实际上最短路线和加工要求中的各项参数有着密切联系，当具体加工零件每圈孔的个数以及孔分布的内外圈半径不同时，最短路线也将出现在不同的方法中。这里可以通过MATLAB软件提供的功能来做具体分析，准确的找到最短路线。

2 数学模型的建立

要利用好MATLAB工具，首要前提就是建立一个合理可行的数学模型。把方法一中刀具所走的路程用L1表示，方法二中刀具所走的路程用L2表示，那么当L1/L2的值大于1时表示方法一的路程长于方法二，而当比值小于1则表示方法一的路程短于方法二。方法一中L1的大小可以根据图3中建立的三角形关系来计算。

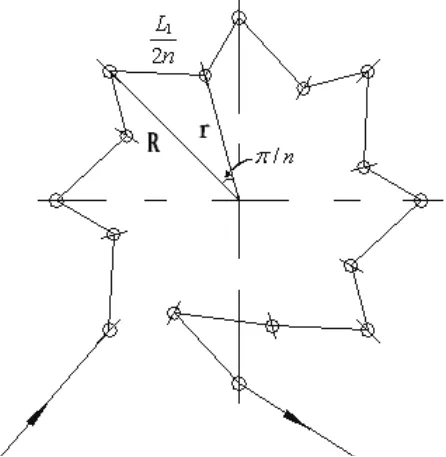
图3 L1的计算分析图

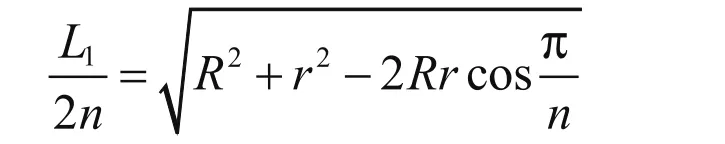
其中

R——外圈半径

r——内圈半径

n——每圈钻孔个数

完整的数学模型如下：

3 MTLABL程序

由于路程的长短受零件参数的影响，这里选取常见参数加以分析。程序中取每圈加工孔的个数从3到20个，内外圈的半径比从0.5到0.95，间隔0.05。实际中如果遇到特殊加工要求只需改变程序中参数的取值，然后利用MATLAB重新计算出两种加工路线的长度比值即L1/L2的值即可。具体程序如下：

4 计算结果

运行程序得到以下计算结果，列表显示如下：

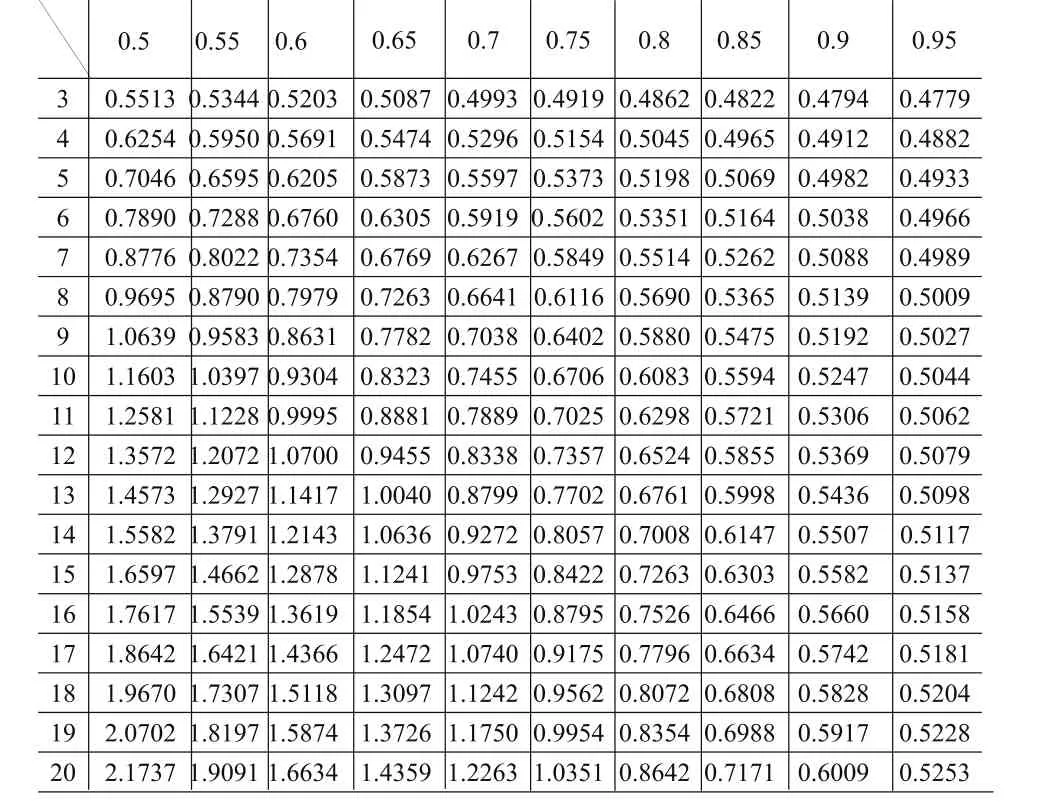
表1 MATLAB计算结果L1/L2

表1中所列数值小于1的表示在其对应的孔数及半径比值下方法一的路程短于方法二，大于1的则表示相反的结果，其分布规律如图4所示。通过观察发现，两种加工方法的刀具路程长短随每圈孔数及半径比值的变化而变化，不能武断的认为在各种情况下都是方法一的路线短。

图4 两种走刀方法路线长短分布图

5 结束语

现今的绝大多数数控工艺教材中，在讲述选取最短走刀路线时，常以此类孔加工问题为例，并给出第一种方法的走刀路线绝对最短的结论。通过分析可知，在内外圈半径相差大，并且孔数多的情况下，往往是第二种方法的走刀路线更短。

借助MATLAB软件进行分析，是准确找出最短走刀路线的可行方法，并且较为便利。通过准确选择最短走刀路线将提高生产加工效率。本文建立的数学模型和编制的MATLAB程序将为分析其他零件的最短加工路线提供借鉴实例。

[1]李华志.数控加工工艺与装备[M].清华大学出版社,2005.

[2]莫愿斌,陈德钊.动态规划粒子群算法解PCB数控钻孔最佳走刀路线问题[J],机床与液压,2006,(08).

[3]陈光明.基于数控加工的工艺设计原则及方法研究[J].制造业自动化,2005,(09).

[4]王贺艳,衡军山.基于MATLAB的三维表面非均布测量数据的可视化[J].机床与液压,2009,(12).