新型折叠装置的优化仿真

张卓辉，李爱军，郝国丹

ZHANG Zhuo-hui, LI Ai-jun, HAO Guo-dan

（中国矿业大学 机电工程学院，徐州 221116）

0 引言

现代服务产业是我国重点支持发展的产业之一，全自动折叠机将床单、被罩等酒店布草自动进行3-5折折叠，大量节省人力，其核心技术为传动带导向布草，利用吹气、翻板和折刀进行折叠动作。作者研发了一种新型折叠装置，对其进行了虚拟样机的仿真分析，实现了敏捷制造。

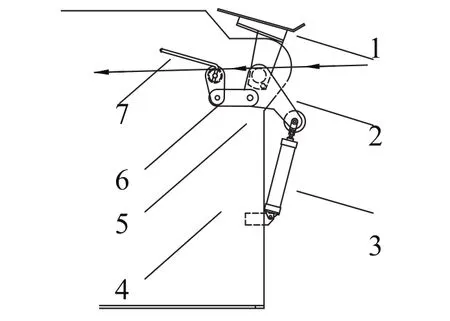
图1 折叠装置结构图

本折叠装置工作原理如图1所示，首先由气缸3推动杆2，杆2则带动刀板1摆动，并通过连杆5带动连爪杆6和导布抓7一起摆动，从而实现布草在水平方向上中间对折。图中箭头方向为布草运动方向。

在现代大型洗涤服务行业，折叠机可以代替人工劳动，大大减轻工人的劳动强度，从而提高生产效率。折叠装置的机构优化设计与运动仿真可以提高设计效率和设计质量，缩短设计周期。基于此，本文将机构的优化设计和运动仿真结合运用，对折叠装置的结构进行优化，并用虚拟样机技术仿真验证优化结果。与优化前相比，简化了弹簧机构为连杆机构，简化了制造工艺。

1 优化设计

1.1 定义设计变量

首先用图2所示的机构运动简图表示图1所示的折叠装置，其四个铰点分别为A、B、C、D，AB、BC、CD和DA的长度分别为l1，l2，l3和l4。其中DA为机架，其长度l4是恒定的。机构起始角根据实际工作角度拟定，分别用θ3和θ1表示。因此，变量可简化为三个，即l1，l2和l3，为三维优化问题，设计变量定义为：

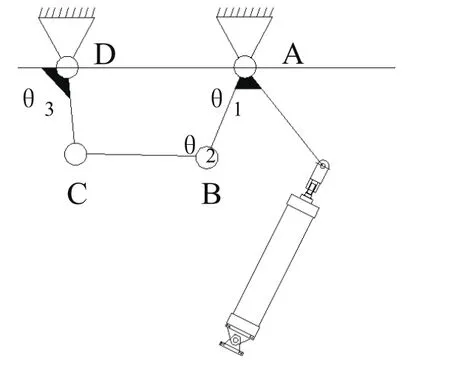
图2 机构运动简图

1.2 建立目标函数

为优化装置结构，以杆件受力最小和杆件质量最小为目标，建立多个目标函数：

1）杆件所受力最小

其中，FAFBFCFD为ABCD四个铰链处所受力。

2）杆件质量最小

由于各杆的材料相同，且横截面积相差无几，所以，要使杆质量尽可能小，应使杆长度尽可能小。

1.3 规定约束条件

考虑机构的动力学特性和结构要求，为使机构具备良好的传力性能，应满足：

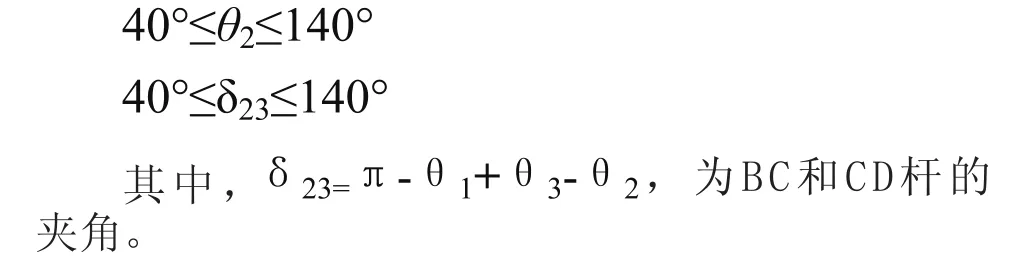
根据折叠装置的实际工作情况，DC杆的摆角为42.01°，如图3的位置分析。

图4 建模装配

1.4 目标函数的简化

由于优化目标多且计算量大，利用计算机强大的运算能力进行初步分析。用SolidWorks/COSMOSMotion软件建立该折叠装置的运动学模型，并对其进行仿真分析。

1.4.1 实体建模装配

在SolidWorks中建立三维装配模型，然后通过添加各种约束创建装配体，如图4所示。

1.4.2 COSMOSMotion仿真

由于该机构的自由度为1，故主动构件数只有一个，为AB杆1。利用step函数表达式模拟气缸的运动，为杆1添加驱动，表达式为：

STEP(TIME,0,0,0.95,0)+ST EP(TIME,0.95,0,1,30D)+STEP(TIME,1.95,0,2,-30D)

这里只模拟一个周期，因此仿真时间为2.0 s。

COSMOSMotion进行运动学仿真，A、B、C、D四个铰点的力如图5(a)(b)(c)(d)所示。从图5的性能参数可以看出，最大力的铰点始终为A点。仿真为下一步的优化设计奠定了理论基础。

图5 ABCD四个铰点的受力图

1.4.3 目标函数的确定

由(b)的分析可知，A点受力一直最大，1.2中的目标函数ABCD四点力尽可能小可以简化为使A点力尽可能小。

本机构优化设计的数学模型为求X=[l1,l2,l3]T

使得：

1.5 模型求解

粒子群算法(PSO)是Kennedy和Eberhart于1995年提出的一种模仿生物觅食行为来寻找最优解的算法，它是从随机点出发同时利用微粒速度与位置上的信息，逐次迭代、最终找到全局最优解的优化算法。由于粒子群算法具有极强的鲁棒性和全局寻优能力，且收敛快，人为干涉少，所以本文采用粒子群算法进行求解。算法步骤如下。

1）初始化粒子群：给定群体规模m，随机产生每个粒子的位置P[i]，初始化每个粒子的速度v[i]=0。

2）计算每个粒子所对应的目标矢量。

3）初始位置P[i]作为每个个体历史最佳位置Pb[i]。

4）初始化迭代代数t=0。

5）筛选粒子群中的非劣解放入外部文档A。

6）循环迭代次数小于等于最大迭代次数M。

由于为2个目标寻优，所以根据用户对子目标的重视程度设定权重系数。计算公式如下：

其中，s1，s2是用户设定的各个目标模型的权重系数，且：s1+s2=1

优化目标是寻找S(X)的最优解，用MATLAB编程，编写粒子群算法程序，按表1的参数设置初始值，计算过程如图6所示，得到了最优解X=[l1,l2,l3]T=[53,60,40]T。

表1 粒子群算法的参数设置

2 仿真验证

图6 F (X)的进化曲线

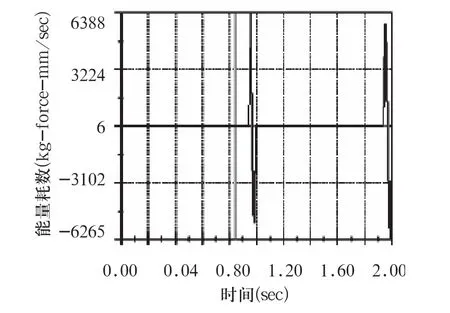
图7 杆1与气缸接头处的力矩曲线

按1.5的优化结果设置参数，X=[53,60,40]T，进行仿真验证。利用SolidWorks尺寸驱动特点，只需修改杆的长度或夹角，装配体会自动更新，即可再次进行仿真。通过改变杆长，以获得杆件所受力尽可能小和杆件质量尽可能小。在改变杆长时，与更改前的仿真结果作为对比，如果增加杆长得到的结果在改善，则继续增大其值，否则减小其值。这样，反复比较修改，就可以获得令人满意的结果。最终获得以下几组优化数据：(a) X=[53,60,40]T，(b) X=[53,40,65]T，(c)X=[54,60,39]T。以(a)组数据为例，图7为杆1与气缸接头处的力矩曲线，该曲线为气缸的选型提供了理论依据。

3 结论

按上述方法对折叠装置进行优化和仿真分析后得到的杆长，在深圳现代后勤集团技术设备研发生产中心制造样机，进行了工业试验。试验结果表明，该装置制造工艺简单，稳定性和可靠性较好，尤其是在折叠厚布有较大的优势，折布效果理想。

1）将机构优化与仿真结合起来，为折叠机构设计提供了一种可视化设计新思路，为机构强度校核计算奠定理论基础，也为系统的动态特性提供理论依据。

2）通过优化设计折叠机构，本方法可行有效，提高设计效率和设计质量，大大降低了成本，带来了十分明显的经济效益。

3）由于铰联接的转动副存在微小的间隙，此间隙会影响机构的平动性，使销轴的受力更为复杂，希望建立销轴的动力学模型。

[1]王洪欣.机械原理[M].南京：东南大学出版社,2008.

[2]孙光永,李光耀,钟志华,等.基于序列响应面法的汽车结构耐撞性多目标粒子群优化设计[J].机械工程学报,2009,45(2)：224-230.

[3]沈世德.实用机构学[M].北京：中国纺织出版社,1997.

[4]SolidWorks公司. COSMOS高级教程[M].北京：机械工业出版社,2008.