数学教学中培养学生创新思维能力的策略探究

杨保瑾

1 巧引问题情景，培养学生学习兴趣

爱因斯坦说：“喜爱是比责任感更好的老师。”为此，笔者设计“设疑引趣——观察分析——归纳总结——实践验证”的教学模式。

如在“等比数列求和”这一节教学中，笔者上课后直接在黑板写上“锡拉和锡塔”，使学生莫名其妙进入问题。学生会思考：今天老师葫芦里到底卖的是什么药？（设疑）

上课前，笔者先给大家讲一个故事：“锡塔是国际象棋发明者，锡拉是印度皇帝，为了奖励锡塔发明国际象棋，锡拉问锡塔希望得到什么赏赐？锡塔回答说：‘在棋盘64格里，第一格给我1粒麦子，第二格2粒麦子，第三格4粒麦子，第四格8粒麦子……依此类推，以后每一格的麦子比前一格的麦子多一倍。’皇帝很爽快地答应了，但皇帝锡拉将全印度的麦子搬来时，都无法满足锡塔的要求。究竟麦子的总数量是多少？”（引趣生疑）

教室内沸腾了，学生露出惊奇的脸色，有的蠢蠢欲动、窃窃私语，更有的迫不及待地伏案计算麦子的总数，却因无法计算出结果而露出失落的神情、求助的眼神（独立思考没有结果）。在学生进入状态时，笔者拿出结果总数“18 446 744 073 709 551 615（粒）”，把学生的求知欲推向高潮。笔者进一步引导学生观察锡塔的要求：棋盘64，第一格1粒麦子，第二格2粒麦子，第三格4粒麦子，第四格8粒麦子……依此类推，以后每一格的麦子比前一格的多1倍。这要求有何特征？学生观察、整理，发现其实是“求数列20，21，22，23…262，263的和”的问题（观察分析）。这是笔者说：“对了，这就是我们今天要学习的内容：求‘等比数列’的和！”学习气氛浓烈，引入新课成功。

通过创设意境使学生的各种感官都参与教学活动，从中培养学生的想象能力和推理能力，真正做到“学生是主体，教师是主导”的教学原则，为进一步开发学生的创造力提供良好平台。

2 巧编数学习题，提高学生创新意识

巧编精选数学习题，使学生先弄清数学习题的功能、结构、方法，通过归纳、分析、批判等方法使学生共同参与，激发学生的创新思维。如在学完“一次方程组解应用题”这一节之后，笔者编选一道传统题目进行练习。

题目：鸡兔同笼，有头45个，脚116只，鸡兔各有几只？

因为思维定势的影响，学生快速运算，得意洋洋地做出解答。

【解】设鸡为x只，兔为y只，依题意，得：x＋y＝45；2x＋4y＝116。解得x＝32，y＝13。

这是常规解法，若是从传授知识，掌握基本方法的要求来说，已经达到目的，但从训练思维角度来说，笔者却没就此止步，对此介绍另一种非常规解法。

师：如果不利用“一次方程组解应用题”，那么解决此题的关键在哪里？

生表现：燥动——相望——疑惑——面面相觑。

师：（引导）关键在于，鸡的2只脚和兔的4只脚在捣乱，如果让鸡兔的脚数是一样多，题目就简单了。令全体兔子起立，举起双手，其他的脚在哪里？余多少？学生哄堂大笑，默想良久：鸡兔的头是45个，脚在下面就有2×45＝90；兔子的手是26，全部都举起来了（116－2×45＝26）。这样一来，兔子是几只？学生经过动手、动脑，很快得出鸡32只，兔13只。最终，比较得出结论：“一次方程组解应用题”更方便，直接快速，达到更佳的教学效果。

3 巧用数学方法，提高学生创新能力

建立数学模型是解决数学应用题的基础。而解决问题的方法以数形结合法、分析综合法最为典型。

【例】甲乙二人相距6 km，二人同时出发，同向而行，甲3小时可追上乙；相向而行，1小时相遇。二人平均速度为多少？

师：同学们进行类比，将甲乙类比成我、你在公路上追赶，并找出关键词画出相关图形。

学生兴趣盎然地讨论，找关键词，动手试画图、列等式、写方程、找结果。

师（引导）：我们用一条直线来表示公路，将你、我走过的路程标在上面，找出其中的关系，列出等式。

学生经过思考、讨论，基本得出关键词：“你我相距6 km”“同时同向”“我追你用3小时”“同时相向”“我与你相遇用1小时”。

师（总结）：用图形（图1）来表示语句，更可以直观地列方程解应用题（数形结合）。

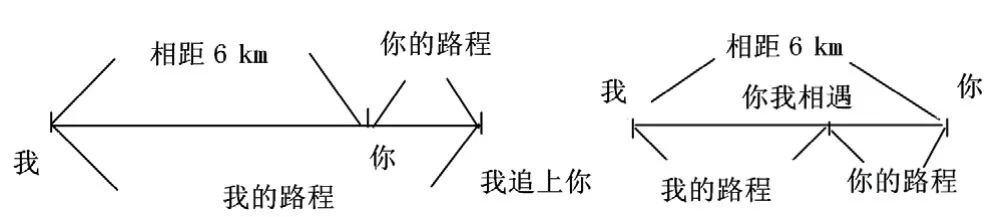
图1

生：相距6 km＋你的路程＝我的路程；我的路程＋你的路程＝相距6 km。

【解】设我的速度为v甲，你的速度为v乙，依题意得：3v乙＋6＝3v甲；v乙＋v甲＝6。解得：v甲＝4 km/s，v乙＝2 km/s。

学生找关键词，画图，标出相应标记的过程，就是学生思维的过程，学生在探索中自我创新能力得到培养，在探索中创新潜能得到发掘。在整个过程中，学生的思维开始与原有的知识产生冲突，并在不断更新、发展、自我完善，形成自己特有的学习方法及思维风格。

透过学生喜悦的表情，说明此方法为他们所接受。他们将抽象的数学问题与具体的实际问题进行相类比，达到图像直观化，从而使学生的认识顺利实现从具体到抽象的思维飞跃，完全符合学生的认知规律。这也是思维能力创新的实践过程。

4 巧演数学习题，提高学生思维创新能力

美国数学家哈尔莫斯说过：“问题是数学的心脏。”其实质是指问题乃是推动数学发展的原动力。

【例】已知a＋b＝8，ab＝4，求a2＋b2的值？

教师引导学生解题前观察已知及结论的特征。

【解】∵(a＋b)2＝a2＋b2＋2ab，82＝a2＋b2＋8∴a2＋b2＝56

当学生解出答案后，教师乘兴追击。

师：大家观察看，若我们将任一已知条件与结论对调，我们的题目会变成什么样？应如何解答？

生：ab与a2＋b2＝56对调有题1：已知a＋b＝8，a2＋b2＝56，求ab的值？

a＋b与a2＋b2＝56对调有题2：已知ab＝4，a2＋b2＝56，求a＋b的值？

师：我们继续观察，看是否能再变题，完全平方公式有多少条等式？

生纷纷说：想到了，还有，还有，比如说，将a＋b改为a－b，其他条件不变不就又有3条了吗？题3：已知a－b＝8，ab＝4，求a2＋b2的值？题4：已知a－b＝8，a2＋b2＝56，求ab的值？题5：已知ab＝4，a2＋b2＝56，求a－b的值？

更有部分学生列举如下例子：已知ab＝4，(a－b)2＝8，求(a＋b)2的值？

学生各抒己见，通过对条件的变换，增强对“两数和平方公式”这一知识点的深入理解，在探索演变的过程中，逐步获取数学方法和数学解题技能技巧，思维得到开拓，创新能力得到培养提高。