H桥整流电路大小信号建模方法研究

关涛 付立军 纪锋 李光磊

(1.海军工程大学舰船综合电力技术国防科技重点实验室，武汉 430033；2. 海军驻九江地区军事代表室， 九江 332007)

目前电力电子技术广泛应用于各种电能变换中，它能够提高能量利用率，减少各种电磁污染而且安全可靠，电力电子应用技术的发展趋势[1,2]是集成化、模块化、智能化、高频化及不断提高装置效率与不断拓展电压应用范围。

为了研究电力电子装置的动静态性能，并设计合适的控制装置，建立电力电子装置可靠的数值模型显得非常重要[3]。电力电子装置是强非线性系统[4]，因此各种变换器动态特性解析模型很难获得。上个世纪70年代以来，众多学者从事这方面的研究并取得了大量成果。应用普遍的SSA[5,6]首先建立各个开关状态下的线性状态空间模型，然后根据各种状态出现的时间权重进行平均，它能够描述状态变量的低频分量，当系统振荡较小时比较实用。在 SSA基础上形成的GSSA[7,8]通过对状态变量进行傅立叶分解建立基于各个傅立叶系数的状态空间平均，从而建立系统大信号模型，其包含变量各阶分量，更全面描述了系统静动态特性。

在GSSA的基础上提出了SSE，直接对开关输入信号与开关函数进行傅立叶分解，将各阶次分量等效成等效电路中的各阶电源模型，采用傅立叶分解级数越高，系统谐波分量描述越完备，仿真精度越高，并在 PSCAD中建立了相应电路模型和解析模型，对其大小信号特性进行分析比较，仿真结果吻合，验证了SSE建模的正确性。

1 建模技术

1.1 SSA

假设系统在一个开关周期T内系统有N种开关状态。在任意开关状态 j下，由于系统中不含有非线性元件，可将其视为线性系统，从而列写在此开关状态下的状态方程；然后根据每个开关状态j在一个开关周期T内的出现的时间权重进行加权，得到状态空间平均模型。下面就H桥整流电路进行分析介绍，电路模型如图1所示假设开关器件为理想器件。

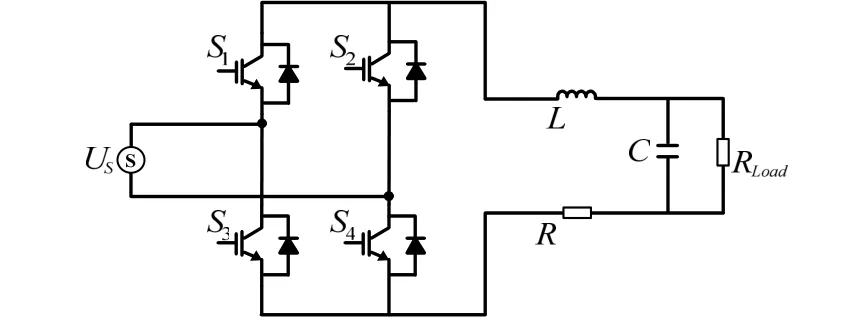
图1 H桥整流电路模型

在此电路中，一个开关周期T内有两种开关状态，开关状态1：S1与S4导通，其他断开；开关状态2：S2与S3导通，其他断开。下面就这两种状态分别进行描述。取电感L电流iL和电容C电压UC为状态变量。

开关状态1，其占空比为d1，其状态方程为：

其中

开关状态2，其占空比为d2(d1+ d2= 1)，其状态方程如下

其中 A2=A1， B2=B1。

然后进行状态平均

下标T代表进行状态平均后的向量。

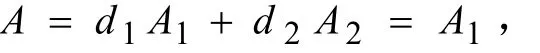
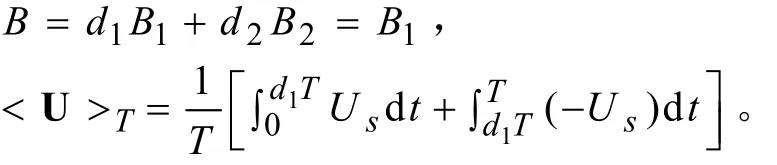
1.2 GSSA

将系统中的周期状态变量x(t)在(t - T, t]内进行傅立叶级数展开，指数形式的傅里叶级数为

其中，ω=2π/T，将xk(t)作为新的状态变量建立系统模型，N取值越大系统高阶分量越丰富也就越精确，但同时提高了系统的阶次。对式(5)求导可得

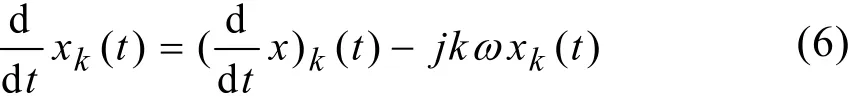
其中(x)(t )为x( t)的k阶傅立叶系数。 k

设电力电子装置的数学模型定义如下

式中x(t)为状态变量向量，u(t)为激励向量，y(t)为输出向量。f(·)和 g(·)可以是线性函数也可以是非线性的，这取决于变换器的类型。对上式两端采用傅立叶级数形式

利用式(6)可得最终的平均模型

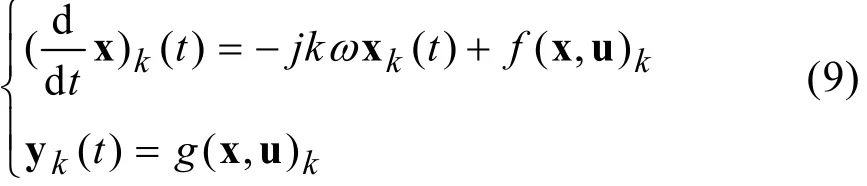
其中下标k表示第k阶傅立叶系数。

由式(5)可知 x (t)= [x (t)]*，假设

k-k

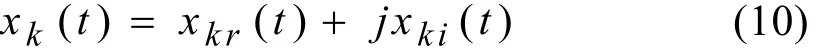
将式(4)进行简化可得

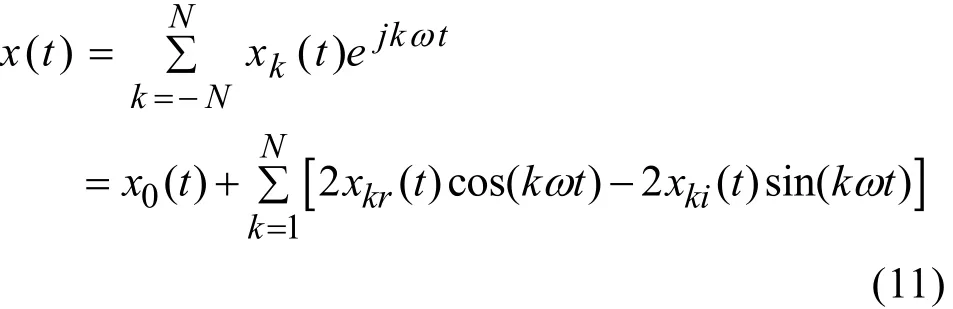
下面将GSSA应用图1所示整流电路，并运用开关函数的概念，假设

该电路的状态方程如下

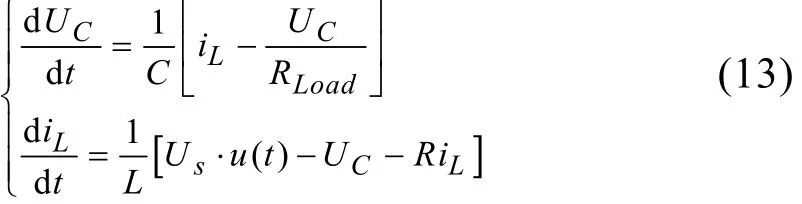
应用式(10)对式(13)运用 GSSA 后可得新的状态方程，其变量分别为 xu kr (t)、 xu ki (t)、 xi kr (t)和 xi ki (t)。

由此可知，该方法可以根据电路的特性要求调整仿真程序的傅立叶分解的阶数，从而提高系统状态变量阶次，因此该方法适用于各种类型的电力电子电路。

1.3 SSE

在图 1中，应用式(12)中开关函数u( t)的概念，对于开关装置交流侧，其电压信号相当于U s ˙u( t)，假设 U s = U m sinωt且开关占空比为50%，对 Us ˙u( t)进行傅立叶分解如下式

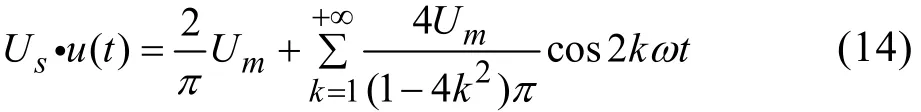
如果将电源与开关装置直接等效成相应的傅立叶分量对应的电源，每个分量相当于一个独立的电源，将各个分量所表示的电源进行串联即为系统的总等效电源，其中第 j个电源电压为U s ˙u( t)的第j阶分量，其中 U s˙u( t)仅含有偶次分量，j为偶数。

由此可得相应的等效电路模型如图2。

图2 等效电路

图2中U0为基波分量，UsN为 Us·u(t)的N阶分量，通过调整N的大小选择仿真电路中UsN的个数，调整系统的仿真精度。一般根据电力电子装置高阶分量大小及分布情况确定。

由此得到的SSE可以描述系统的高阶分量，并用等效电路的方式建模，这样更有利于实际电路的仿真分析。N取为0时由该电路得到的状态方程和SSA完全一致，N相同时其描述的模型与GSSA完全一致。但是比较以上两种方法，该方法更简单直观，而且效率高，误差小，易于实现。

2 验证

在PSCAD中建立了如图1所示电路模型、SSA数学模型、GSSA数学模型和SSE数学模型，其中 L=3.0 mH，C=100 µF，RLoad=1 Ω，R=1 Ω，开关占空比D为50%。对这四种模型分别进行大小信号仿真模型验证，GSSA模型N = 2和SSE模型中N = 4。本文对四种情况进行了分析：(1)电源电压幅值由10 V上升到100 V；(2)L由3.0 mH降低到0.3 mH；(3)C由100 µF上升到1 mF；(4)负载电阻RLoad由1 Ω上升到10 Ω。具体的波形分别如图3、图4、图5与图6所示。图中CM表示图1所示电路仿真模型波形。

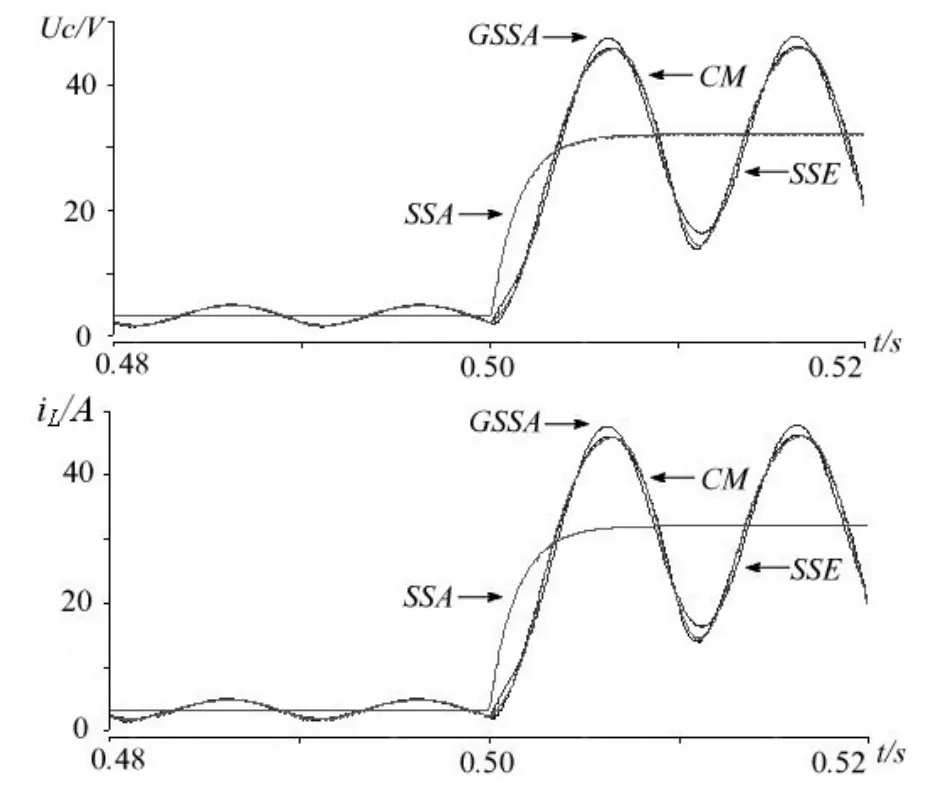
图3 电源电压幅值由10 V上升到100 V时

图4 L由3.0e-2 H降低到3.0e-3 H时

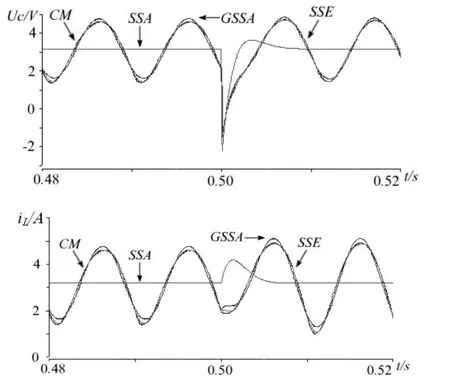
图5 电容C由1.0e-3F降低到1.0e-4F时

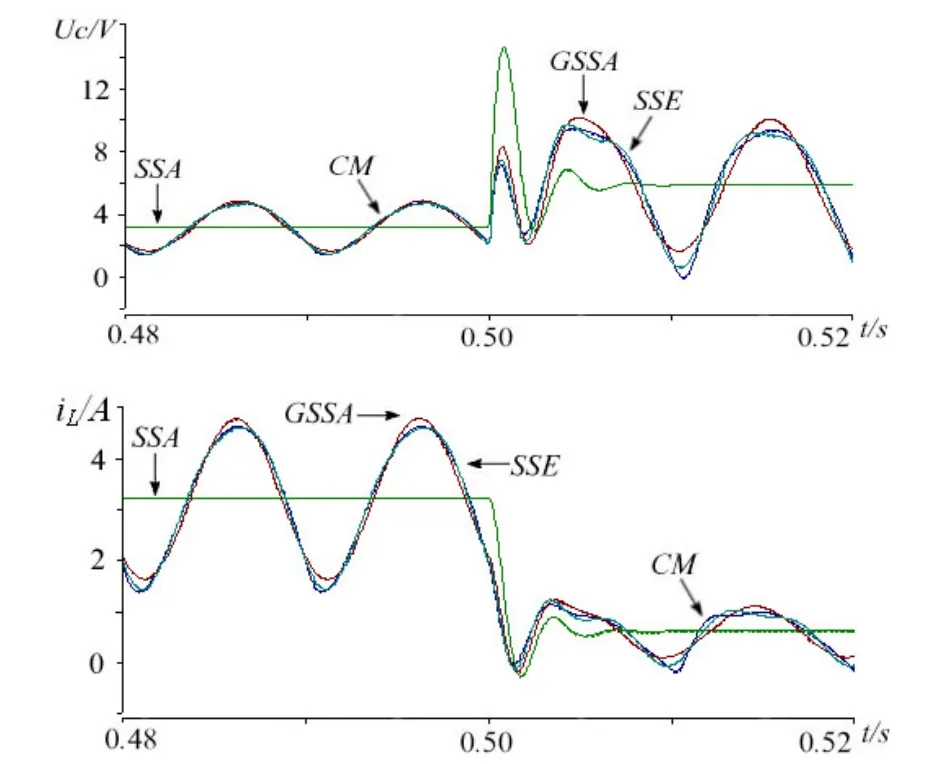
图6 负载电阻RLoad由1 Ω上升到10 Ω时

由图3到图6的波形可知，以上三种方法中SSA模型仅能描述系统的直流分量，不能够描述系统的谐波分量，该方法应用局限性强，仅应用于直流分量起主要作用的情况；GSSA模型和SSE模型在数学模型上一样，得到的波形与系统仿真结果吻合，能够完整的描述系统的振荡分量，误差不到1%，由此可知H桥整流电路中GSSA模型和SSE模型描述系统特性效果相同。图中SSE的波形比GSSA更加精确，这是因为SSE仿真阶次比GSSA高，由此可得系统阶次越高仿真结果越准确。而在实现上GSSA系统阶次高，其状态变量SSE的两倍，计算复杂；SSE建模方便，仿真效率高，易于实现。

当把GSSA的谐波阶次N取为0时，得到的波形与SSA完全一样，由此可知SSA只是GSSA的一种特殊形式；对于后两种方法，当N取为4时系统波形比N取为2与0时精确，对于高次谐波比较严重的情况下这种区别会更加明显，由此可知模型阶次越高波形越精确，描述的暂态过程更准确，但系统模型变得比较复杂，仿真时间消耗越大。实际应用中应选择合适的阶次进行建模。

3 结束语

本文介绍了SSA和GSSA的应用原理，并说明了它们的区别与应用范围；针对一些电源和开关直接串联的电路，提出了SSE，将电源与开关直接等效成与各阶次傅立叶分量相同的电源的串联，得到的结果与GSSA描述的模型完全一致，但该方法更加简单直观，计算效率更高，更易于实现。最后通过对H桥整流电路模型分析建立其大小信号数学模型，在 PSCAD仿真软件中验证了SSE建模的正确性。

:

[1]Thomas G Wilson. The Evolution of Power Electronics[J]. IEEE Trans on Power Electronics,2000, 15(3): 439-446.

[2]Bimal K Bose. Energy, Environment, and Advances in Power Electronics[J]. IEEE Trans on Power Electronics, 2000, 15(4): 668-701.

[3]Hadi Y Kanaan and Kamal Al-Haddad. Modeling Techniques Applied to Switch-mode Power Converters: Application to the Boost-type Single-phase Full-bridge Rectifier[J]. HSI 2008, 2008:979-983.

[4]张波. 电力电子学亟待解决的若干基础问题探讨.电工技术学报，2006，21(3)：24-35.

[5]R D Middlebrook and S Cuk. A General Unified Approach to Modeling Switching-converter Power Stages[J]. IEEE PESC, 1976: 18-34.

[6]S Cuk and R D Middlebrook. A General Unified Approach to Modeling Switching DC-TO-DC Converters in Discontinuous Conduction Mode[J].IEEE PESC, 1977: 36-57.

[7]Sanders S R. Generalized Averaging Method for Power Conversion Circuits[J]. IEEE Trans. on Power Electronics, 1991, 6(2): 251-259.

[8]T Demiray, F Milano and G Andersson. Dynamic Phasor Modeling of the Doubly-fed Induction Generator Under Unbalanced Conditions[J]. IEEE PowerTech 2007, 2007: 1049-1054.