永磁同步电机弱磁调速系统建模及仿真研究
张树团 李伟林 鲁芳 张海鹰
(1. 海军航空工程学院控制工程系,山东 264001; 2. 西北工业大学自动化学院,西安 710072)
1 引言
永磁同步电动机(PMSM)具有效率高、转动惯量小等优点,在高性能的调速传动系统中有良好的应用前景。但是永磁同步电动机在恒功率运行区域,随着转速升高,由于供电电压的限制及电流控制器的饱和影响,严重损害PMSM的电磁转矩性能,难以提高弱磁运行范围。本文针对永磁同步电机矢量控制系统,着重研究分析如何提高其弱磁调速的恒功率调速比,提出了一种基于电流调节的PMSM定子磁链弱磁控制算法,保证永磁同步电机在整个弱磁调速区以最大转矩电流比运行。其q轴电流由外部转矩、转速给定和母线电压值的变化来决定,d轴电流分量则由q轴电流值和转速值来决定。在Matlab/Simulink中建立了PMSM弱磁控制系统的仿真模型,仿真结果表明,该弱磁控制算法有效地拓展了永磁同步电机的恒功率从调速范围。
2 永磁同步电机数学模型
以二相导通星形三相六状态为例,分析PMSM的数学模型及转矩特性。为建立永磁同步电动机的转子轴(dq轴)数学模型,作如下假定:
(1)三相绕组完全对称,气隙磁场为正弦分布,定子电流、转子磁场分布对称;
(2)忽略齿槽、换相过程和电枢反应等影响;
(3)电枢绕组在定子内表面均匀连续分布;
(4)磁路不饱和,不计涡流和磁滞损耗。
则三相绕组的电压平衡方程式可表示为

式中,ua,ub,uc为定子绕组的相电压;
Rs为定子每相绕组电阻;
ia,ib,ic为定子绕组相电流;
Ls为定子每相绕组的自感;
M为定子每相绕组的互感;
p为微分算子p=d/dt;
ψf为转子永磁体磁链;
θ为转子位置角,即转子q轴与a相轴线的夹角。
因为三相绕组为星型连接,有ia+ib+ic=0,则式(1)可简化为:
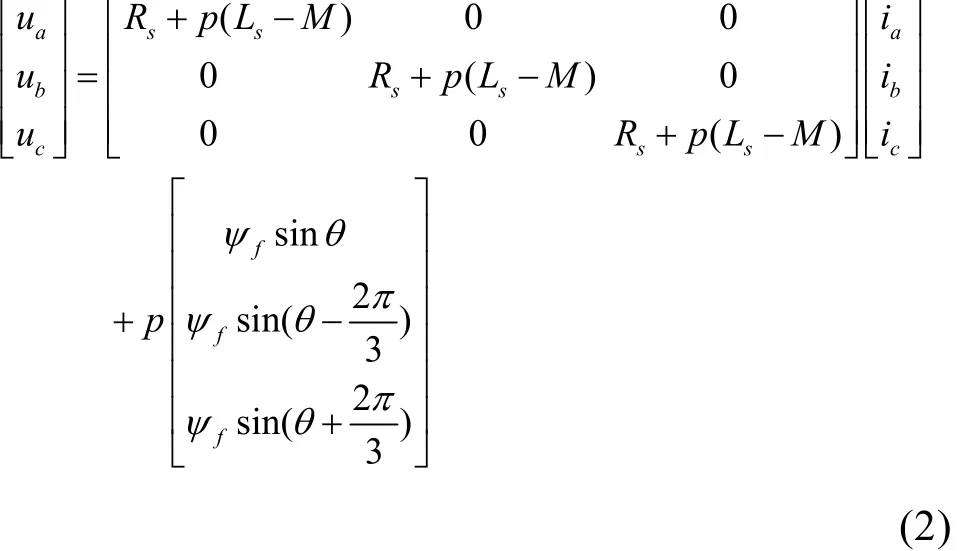
式(2)为永磁同步电机在abc静止坐标系下的电压方程。利用坐标变换,把abc静止坐标系变换到dq转子坐标系,得到相应的动态电压方程:
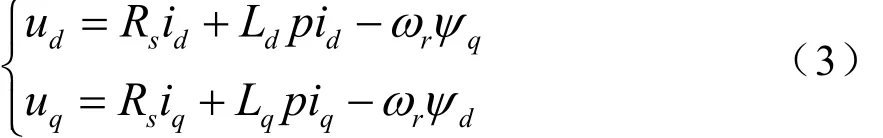
式中,ωr为转子电角速度;Ld、Lq为直、交轴同步电感。
在d、q坐标系下电机的电磁转矩为:
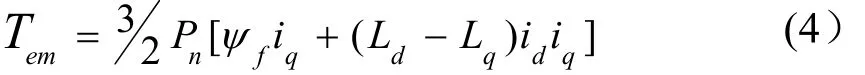
式中,Pn表示电机极对数。
3 弱磁控制原理
永磁同步电机中,感应电势随着转速的增加而增加,当电机的端电压达到控制器直流侧电压时,PWM控制器将失去追踪电流的能力。因此定子端电压Us和相电流Is,受到逆变器输出电压和输出电流极限(Usmax和Ismax)的限制。由此可得电流极限圆

电压极限椭圆
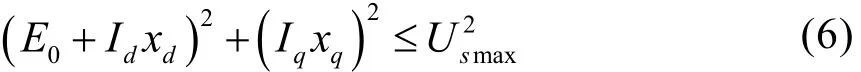
又因为E0=ωψf,xd=ωLd,xq=ωLq,所以电压极限椭圆方程可以改写为
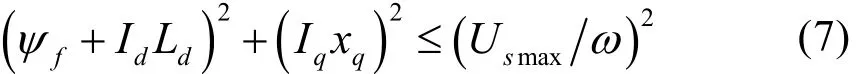
永磁同步电动机的运行范围是受以满足电流极限圆和电压极限椭圆为条件限制的,即电机的电流矢量Is(其分量为Id与Iq)应处于两曲线共同包围的面积内,如图1中阴影部分所示。由图1可以看出,电机转速ω升高,Id分量趋于增大,相应的Iq分量必须减小,因此,电机的电磁转矩也随转速升高而下降,显示出恒功率的特性。
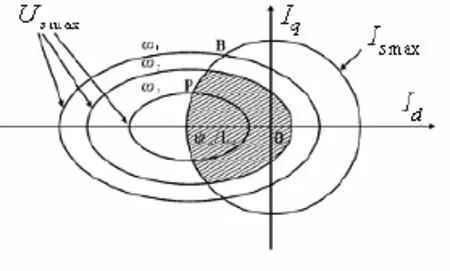
图1 PMSM电压电流限制曲线
4 基于Matlab的PMSM弱磁控制系统仿真模型建立
在Matlab6. 5的Simulink环境下,利用SimPower2 System Toolbox2. 3丰富的模块库,在分析PMSM数学模型的基础上,提出了建立PMSM弱磁控制控制系统仿真模型的方法,弱磁控制系统总体设计框图见图2。
PMSM弱磁控制建模仿真系统采用双闭环控制方案:速度环为控制外环,它使电机的实际转速与给定的转速值保持一致,实现电机的加速、减速和匀速运行,并且及时消除负载转矩扰动等因素对电机转速的影响。电流环为控制内环,它的作用是控制逆变器在定子绕组上产生准确的电流。根据模块化建模的思想,将图2中的控制系统分割为各个功能独立的子模块,其中主要包括:PMSM本体模块、矢量控制模块、电流滞环控制模块、速度控制模块、弱磁控制模块等,通过这些功能模块的有机整合,就可在Matlab/Simulink中搭建出PMSM控制系统的仿真模型,并实现双闭环的控制算法。
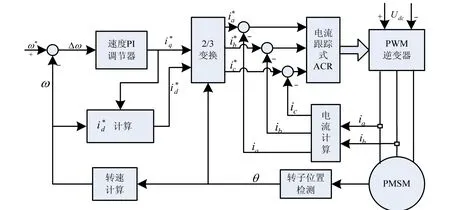
图2 PMSM弱磁控制系统总体设计框图
4.1 PMSM本体模块
在整个控制系统的仿真模型中,PMSM本体模块是最重要的部分。Matlab/ Simulink的工具箱提供了按交直轴磁链理论建立的定子绕组按Y型连接的 PMSM 模块。PMSM模块共有四个输入端,其中前三个输入端,分别为A相、B相、C相输入端,第四个输入端为转矩输入端T1(N·m)。当T1>0时,为电动机模式;当T1< 0时,为发电机模式。PMSM的主要设置参数包括:定子电阻R(Ω);交直轴定子电感Ld, Lq(H);转子磁场磁通Ф (Wb);转动惯量 J(kg·m2);粘滞摩擦系数B(N·m·s);电机的极对数 p 等。
4.2 矢量控制模块
dq向abc转换模块主要是根据转子的位置角即图2中的θ,按照dq变换的反变换公式产生三路基准信号,dq变换的反变换公式如下
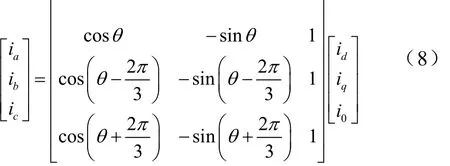
式(8)中包含了零序分量,在对称三相条件下,没有零序分量,dq向abc转换结构框图如图3所示。dq向abc转换模块输出三路基准信号,该曲线的横坐标按转子位置标注,纵坐标按电流标注。三根曲线分别代表对应与转子的某一位置的三个绕组各自驱动电流瞬时值,通过矢量合成可知此刻的旋转磁场矢量的角度。
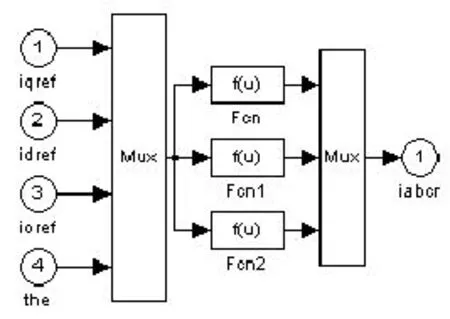
图3 dq到abc转换结构框图
4.3 电流滞环控制模块
三相电流源型逆变器模块是按照矢量控制理论,利用滞环电流控制方法,实现电流逆变控制。输入为三相参考电流和三相实际电流,输出为逆变器电压信号,模块结构框图如图4所示。
当实际电流is经过惯性环节1/Ts+ 1低于参考电流isr且偏差大于滞环比较器的环宽时,电机对应相正向导通,负向关断;当实际电流is经过惯性环节1/ Ts+ 1超过参考电流isr且偏差大于滞环比较器的环宽时,对应相正向关断,负向导通。选择适当的滞环环宽,即可以实际电流不断跟踪参考电流的波形,实现电流闭环控制。
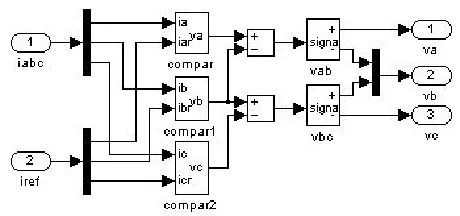
图4 三相电流源型逆变器模块结构框图
4.4 速度控制模块
速度控制模块的结构较为简单,如图5所示,参考转速和实际转速的差值为单输入项,三相参考相电流的幅值iqref为单输出项。其中,Ki为PI控制器中P(比例)的参数,K/T1为PI控制器中I (积分)的参数,饱和限幅模块将输出的三相参考相电流的幅值限定在要求范围内。
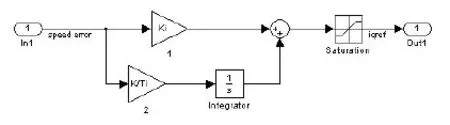
图5 速度控制模块结构图
4.5 弱磁控制模块
电机在恒转矩区运行时,直轴电流i*q的计算公式如下
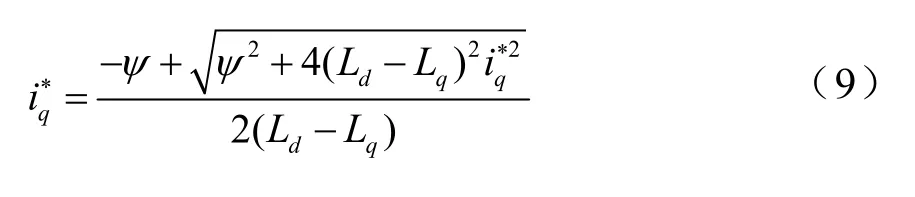
电动机转速超过基速时,恒功率运行,i*d切换为下面公式计算
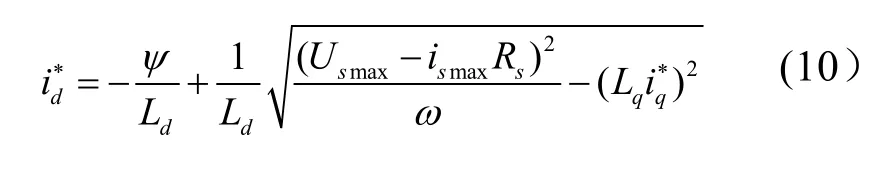
式中,Ld为永磁同步电机直轴电感;Lq为永磁同步电机交轴电感;Rs为定子绕组的电阻;ω为感应电动势的电角度。
5 仿真结果
在前面理论分析的前提下,本文基于Matlab/Simulink建立PMSM弱磁控制系统的仿真模型,并对该模型进行了PMSM双闭环控制系统的仿真。PMSM电机仿真参数设置:相绕组电阻R为2.87 Ω,极限电压值Usmax为240 V,d轴电感分量Ld为388.5 mH,极限电流值Ismax为1.6 A,q轴电感分量Lq为475.5 mH,起始机械转矩Ti为5 N•m,永磁磁链ψM为447,机械转矩变化时刻t为0.015 s,极对数p为4,最终机械转矩Tend为3 N•m。通过仿真试验表明,转速达到基本转速以后,若不加该电流弱磁控制算法,继续升速的空间很小。采取了本文提出的电流调节算法以后,永磁同步电机的弱磁调速区域明显扩大,恒功率运行区域调速比达到了4:1;最高转速达到2200 rad/s,转速为1600 rad/s时的仿真波形如图6到图8所示。
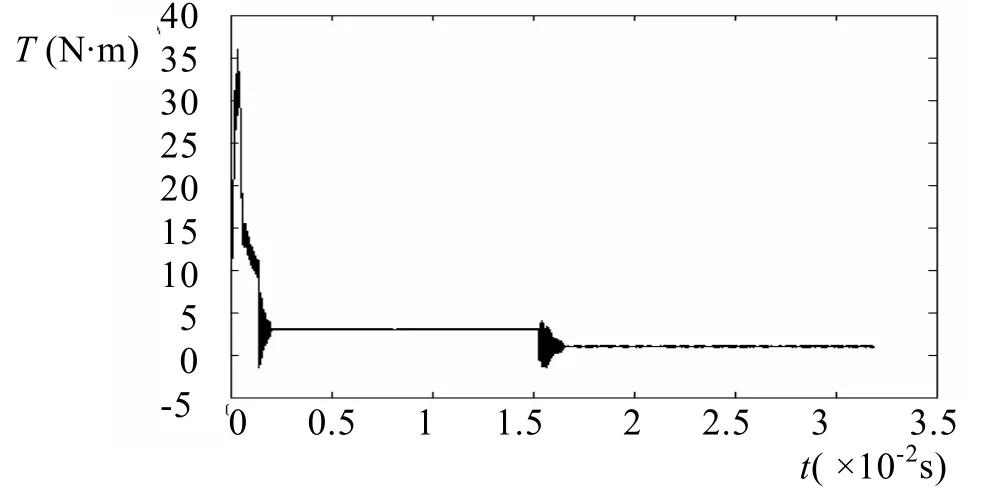
图6 转矩响应曲线
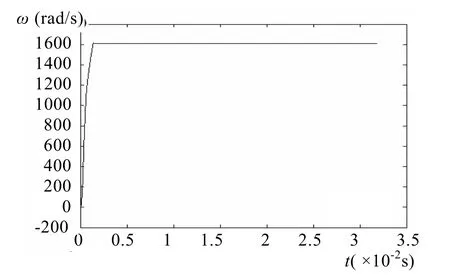
图7 转速相应曲线
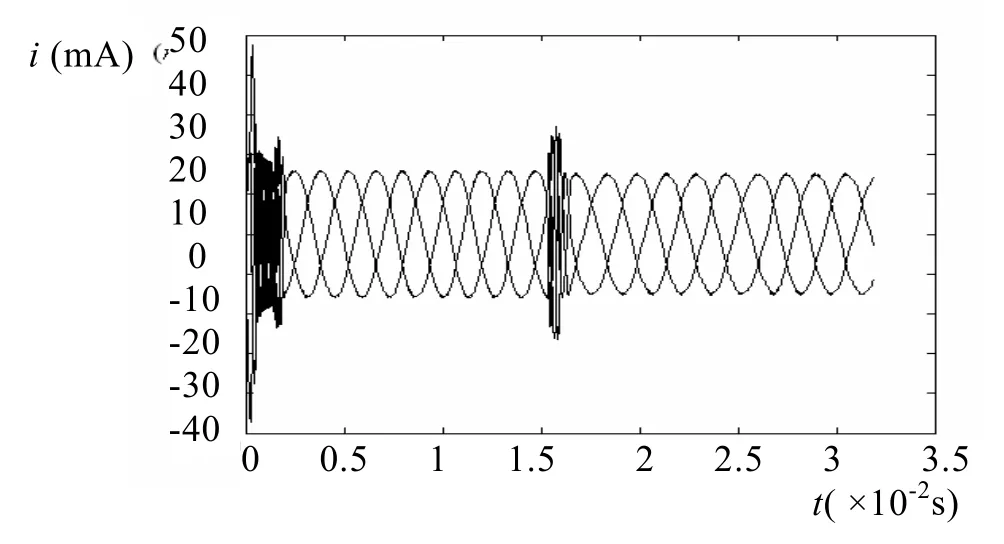
图8 三相电流仿真波形
由仿真波形可以看出:在转速为1600 rad/s时,系统转矩响应快速且平稳,三相电流波形较为理想,转速响应快且稳态运行时无静差,具有较好的静态和动态特性。
6 结束语
本文在分析 PMSM 数学模型的基础上,提出了一种基于电流调节的 PMSM 定子磁链弱磁控制算法。仿真实验结果表明,本文提出的方法拓宽了电动机弱磁调速范围,有效地提高了恒功率运行区域的调速比,转速响应迅速,转矩变化平稳,系统具有良好的动态和稳态性能,达到预期的设计指标要求。采用该PMSM仿真模型, 可以便捷地实现、验证电流调节的弱磁控制算法,也可对其进行简单修改或替换,完成控制策略的改进,通用性较强。
:
[1]A.K; Sulkowski ,W.; Aga, L. A. ;Norum, L. A Fully Digital Permanent Magnet Synchronous Motor Drive with Flux Weakening Adnanes.[J]. Electrical Machines and Drives, 1991. Fifth International Conferenceon (Conf. Publ. No. 341)1991, (341):11-13.
[2]Ho, P. K.; Lee, C. K.. Modeling and Simulating of a Permanent Synchronous Motor Under the Flux-weakening Control[J]. Industrial Electronics,1998. Proceedings. ISIE′98. IEEE International Symposiumon, 1998, (2): 462-467.
[3]Sozer, Y.; Torrey, D. A. Adaptive Flux Weakening Control of Permanent Magnet Synchronous Motors[J].Industry Applications Conference, 1998. Thirty-Third IAS Annual Meeting. The 1998 IEEE, 1998,(1):475-482.
[4]许强, 贾正春, 许锦兴. 作主轴传动的永磁同步电机弱磁控制系统[J].华中理工大学学报,1993,21(2):31-36.
[5]冷再兴, 马志源. 一种新的内置式永磁同步电机弱磁调速控制方法[J].微电机,2006,39(6):11-14.
[6]唐任远. 现代永磁电机理论与设计[M]. 北京:机械工业出版社,1997.
[7]张平. .MATLAB基础与应用简明教程[M]. 北京:北京航空航天大学出版社,2001.
[8]Shigeo Morimoto, Yi Tong, Yoji Takeda, et al. Loss Minimization Control of Permanent Magnet Synchronous Motor Drives[J]. IEEE Trans. on Industrial Electronics, 1994, 41(3):511-516.
[9]Chan C C, Chan K T. An Advanced Permanent Magnetic Motor Drive System for Battery-powered Electric Vehicles[J]. IEEE Trans. on Vehicular Technology, 1996, 45(1):180-188.
[10]Sadegh Vaez, M A Rahman. Adaptive Loss Minimization Control of Inverter-fed IPM Motor Drives[J]. IEEE Conference of PESC'97 Record,1997,35(5):861-868.

