蚁群算法在铁路乘务运用计划编制中的应用研究

郑金子，苗建瑞，张君平

（北京交通大学交通运输学院，北京100044）

现阶段我国铁路现场的乘务运用计划仍然采用手工编制方法，这种方法不仅效率很低，而且由于受到编制人员的主观因素影响，所编制计划的质量很难保证，因此手工编制方法势必会成为高速发展的铁路运输事业的制约因素。如何运用计算机有效、合理地编制乘务运用计划成为现阶段亟待解决的问题。

1 乘务运用计划

参照既有铁路机车交路和乘务员工作安排办法以及国外高速铁路乘务组织措施，我国铁路未来的乘务方式将以轮乘制为主，其乘务员运用计划的手工编制过程主要分为下面几个阶段：

（1）确定乘务员基地（乘务员所属部门，高速列车始发、终到作业的地区）及可以换乘的车站（或乘务折返地）；确定各乘务员基地的任务；给定乘务工作要执行的列车运行图。

（2）以乘务员可能换乘的车站为分割点，将运行图中的运行线分割成乘务区段，例如，将图1中运行线x、y、z分割成{x1，x2}、{y1，y2}和{z1，z2，z3}等几个区段。

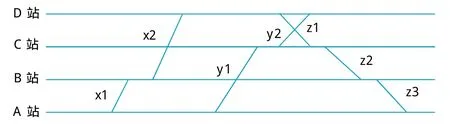
图1 运行线分割成乘务区段

（3）按照乘务员一次乘务总时间、乘务折返接续时间等乘务规则，将各乘务区段组合成不同的可行乘务交路，作为最终乘务交路备选方案。例如，图2中B站为乘务员基地，{1，3，5，7}、{2，4，6，8}、{9，11}分别组成了3个不同的可行乘务交路，而乘务区段{1，3，5，9，11}组成的则是不可行乘务交路（一次乘务时间超过了乘务规则规定的时间），见图2。

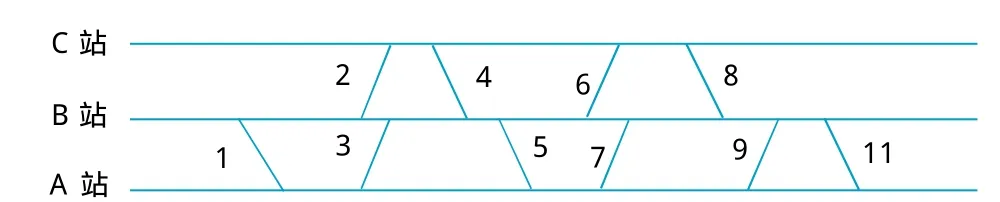
图2 乘务交路

（4）根据评价标准，选择比较优化的乘务交路，作为乘务组一次乘务工作内容。所有被选择的乘务交路集合，必须完全覆盖全部乘务区段，乘务交路的数量就是每日所需要的乘务组数。乘务组每一次工作就是完成一个乘务交路，在乘务中不能中断或更换乘务组，这样就构成可行的乘务交路计划。由于满足乘务规则的乘务区段的可能组合方案数量很多，即乘务交路方案数量很多，可以构成不同乘务交路计划方案，例如，表1所示的以图2为基础的4个不同方案，且各方案之间存在着优劣差别，方案1明显优于方案4；见表1。

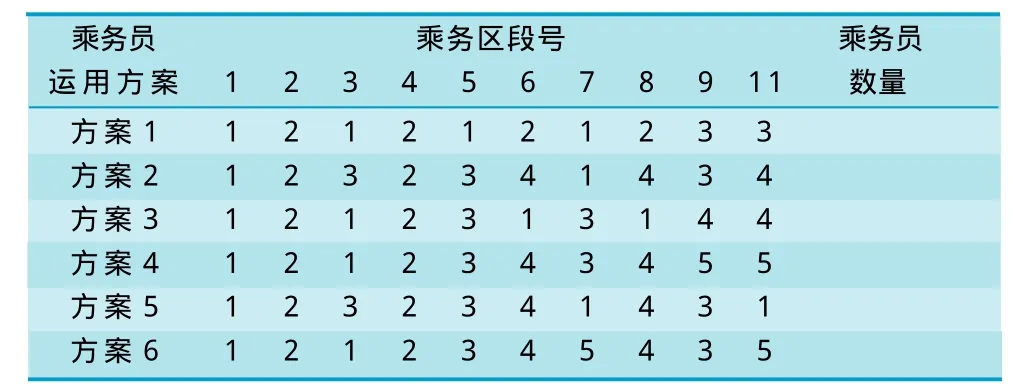
表1 乘务员运用计划案例

在乘务员运用计划编制中，要检查大量的乘务规则，需要花费大量的时间，而如何选择能够覆盖所有乘务区段的乘务交路以形成最优运用计划，是优化编制乘务员运用计划的关键。

将蚁群算法引入乘务运用计划的编制是一种开新的尝试。把路网中的乘务区段抽象成带有权值的点，把每站的接续时间抽象为带有权值的边。点和边相连，构成了乘务工作的网络，进而抽象成为一个类似K-TSP的问题，即在满足工作时间的条件下，用最少的接续时间（为了提高时间的利用率，将总接续时间最短作为目标函数），遍历网络中所有的点。

2 建立模型

在编制乘务运用计划时要以列车运行图为基础：（1）确定乘务基地和换乘点；（2）以乘务员可能的换乘站为分割点将运行线路分成若干乘务区段；（3）按照乘务规则将这些区段组合成可行的乘务交路，作为备选方案；（4）根据一定的评价标准在若干备选方案中选择比较优化的交路作为一个乘务组的工作内容，要求所选的交路的集合必须覆盖所有乘务区段，乘务交路的数量就是每日所需的乘务组数，这样就构成了可行的乘务交路计划。铁路乘务运用计划编制需要满足以下约束条件：

（1）同一时间每人最多只能执行一个班次。

（2）每个班次只能由一个乘务组执行，且任务一旦开始被执行就不能中断直至执行完毕。

（3）满足班次衔接要求，即前一个班次的终止站应该为下一个班次的起始站。

（4）满足人员工作时间的要求，如总乘务时间、纯乘务时间和最大接续时间等要求。

本文采用人员利用率最高，即满足约束条件下总空闲时间最少为目标构造相应的数学模型，如下所示：

在上述模型中，（1）为目标函数；约束条件（4）和（5）保证每个任务点都只被一个人执行；（6）为总乘务时间的限制；（7）为班次间隔时间约束，保证完成前面的任务才能进行下一任务。

3 算法构造

3.1 解的构造

首先根据列车运行计划构造图，图中的点表示乘务区段，点的权值表示该区段的运行时间；图中的有向边对应着两个区段之间的接续，边的长度为满足接续条件的两个区段之间的接续时间。

在求解乘务运用计划问题的蚁群算法中，采用k只蚂蚁共同构造一个可行解，则这k只蚂蚁组成一组；在该算法中，将会有m组蚂蚁（即m＊k只蚂蚁）共同协作寻找最优解。（1）对于第i（i=1,2,…m）组蚂蚁，为该组的第1只蚂蚁随即分配一个点，这只蚂蚁从该点出发按照一定的搜索规则访问其它的点，直到不再满足约束条件便停止搜索，将该蚂蚁所访问过的点从图中删除，同时为该蚂蚁分配一个子周游列表（j为蚂蚁编号），该表记录了这只蚂蚁访问过的点。（2）引入另一只蚂蚁遵循第1只蚂蚁的行为在剩下的点中继续搜索；直到图中所有的点都已被删除，第i组蚂蚁的搜索行为停止。所有的子周游列表的集合,……,}（i=1,2,……,m；x为该组中蚂蚁的个数）便构成了本问题的一个可行解。（3）在m组蚂蚁所构成的m个可行解中根据目标函数选出最优解。

3.2 蚂蚁的路径选择

τij(t)表示t时刻在点i, j连线上残留的信息素。初始时刻，各条边上的信息素相等，设τij(t=0)=C(C为一常数)，蚂蚁k在运动过程中根据各条边上的信息素大小决定转移方向表示在t时刻蚂蚁k由点i转移到点j的概率：

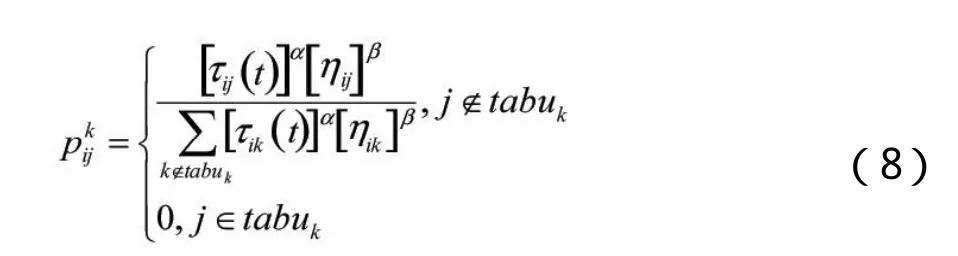
其中，ηij为启发式信息，表示蚂蚁从点i转移到点j的期望程度，本文中取ηij=1/dij（dij表示点i到点j的距离），α为在路径ij上残留信息的重要程度，β为启发式信息的重要程度，集合tabuk为禁忌表，tabuk= {H1i, H2i,……,Hxi}。

3.3 信息素的更新

每一组的所有蚂蚁都完成周游之后，该组中的蚂蚁所经过的径路上的信息素要根据下式进行调整：

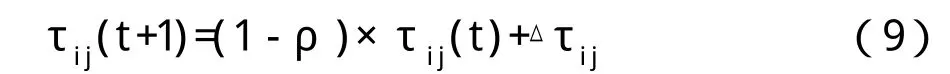
其中， ρ表示信息素的蒸发系数，△τij为本次周游中边ij上的信息素增加量，如果边ij没有被任何一只蚂蚁走过则△τij取零；否则令△τij=Q/L ，其中Q为常数，L为该组所有蚂蚁所经过的边长之和。

3.4 该算法的具体步骤

（1）初始化各条边上的信息素，令τij(t=0)＝C（C为常数）；N＝0（N为迭代次数）。

（2）给第i组的蚂蚁k随即分配一个起点a；如果满足约束条件则继续选择下一点，根据转移概率公示计算和a点满足接续关系的所有边的Pij，找到max(Pij)以得到a的下一点b，并将蚂蚁k移动到b点；将点a和点b从图中删除并存储到蚂蚁k的周游列表中。

（3）如果蚂蚁k找不到符合条件的点，则停止搜索并引入一只蚂蚁，即k=k+1,再转至（2）。

（4）如果tabuk中存放点的个数等于初始图上的点数，则该组蚂蚁搜索停止。

（5）记录蚂蚁个数m=k，计算所有蚂蚁走过的边长之和L和目标值Z。

（6）按照式（9）更新信息素。

（7）迭代次数N＝N+1，如果N小于预定的迭代次数W，转至（2）。

（8）当N＝W时，所有迭代结束。求min(Z)即可得到最优解并输出，算法结束。

3.5 算法流程图

算法流程见图3。

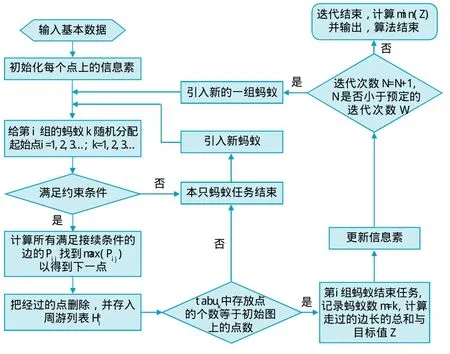
图3 算法流程图

4 试验结果及分析

4.1 试验结果

为了检验算法的可靠性和效率，用C++语言编写了程序并在VC的平台上使该算法得以实现。运用的测试数据是京广线部分路网的数据，包括149个节点（代表乘务区段）和1 510条边（代表乘务区段间的接续）。（测试数据和关键程序代码见附录）程序运行的界面和部分输出结果如图5。

图5 部分输出结果

4.2 结果分析

通过结果看出，该程序能够较为合理的求解到最优解或近似最优解，相对于人工编制乘务计划而言工作效率有了显著的提高。然而，在程序运行过程中也发现了一些不足。程序运行效率不高，如果蚂蚁组的迭代次数为100次，需要平均运算时间为12 s；如果将迭代次数改为200次，则平均需要24 s的运算时间。产生这种现象的原因有：（1）设计的算法的逻辑结构不是很合理，存在一些重复或是无效运算，这是造成算法效率低的最重要原因；（2）由于初次接触蚁群算法，对算法中所用的参数没有进行过深入研究，只是运用前人的经验数值，而这些参数并不一定符合所面临的问题特征，因此降低了算法的效率。（3）不足点就是由于编程水平有限和时间紧迫，软件的设计过于简单，没有实现最初预想的在输出界面显示运算结果这样一种功能，而只能是在程序运行结束后到“结果.txt”文件中去查询，在实际运用中很不方便。以上不足都是我们在进一步的学习以及程序设计等工作中需要特别注意并及时改正的。

5 算法收敛性判定

收敛性是评定一个算法质量高低的重要指标之一，因此为了进一步提高该算法的质量，用自制的“乘务计划编制软件”做了大量的试验，用来观察在这100次迭代中总接续时间的变化情况。通过分析认为，在蚁群算法中信息素起到了非常重要的作用， 它直接决定了蚂蚁在搜索路径中的转移概率。由公式（8）可知，每条边上的t＋1时刻的信息素是该边上t时刻的信息素加上本次循环中增加的信息素△t，而△t是由常数Q和蚂蚁在一次循环中所走路径长之和决定的。可见，每条边上的初时信息素大小和常数Q的选择是决定该算法收敛性的两个重要因素。而初始信息素和Q二者之间又存在着一定的制约关系，因此在本次试验中将各条边上的初始信息素赋予一个较小的常数1，通过不断改变Q值观察算法的收敛效果以确定最合理的Q值。在一些相关文献中，Q值被设为10，将取值范围定为0到100之间的整数， 并通过大量的试验发现当Q值为10到30之间的整数时算法的收敛效果相对更好一些，并且当Q＝20时算法的收敛性能最好。见图6。

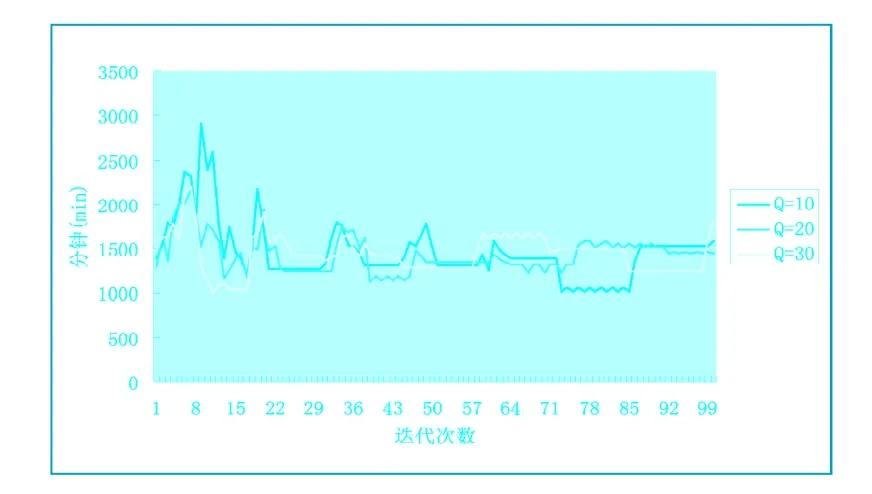
图6 算法收敛曲线

6 结束语

本文探讨性的研究了蚁群算法在铁路乘务运用计划编制中的应用问题，通过编程实现了该算法，并对算法的效率进行了测试，得到了相对理想的结果，在此基础上还开发了计算机编制乘务计划的小软件。运用此软件能够根据具体的运营情况制定出符合实际的乘务运用方案，这对于提高铁路乘务人员调度工作的效率、降低乘务工作的成本起到了一定的作用。

[1] 赵鹏. 高速铁路动车组和乘务员运用的研究[D] . 北京：北方交通大学，1998.

[2] 赵鹏，胡安洲，杨浩. 机车乘务员运用计划的优化编制. 铁道学报，1998. 20（4）：8-11.

[3] 赵鹏，姚凤金，张洪亮. 综合调度仿真系统中的机车乘务调度计划的编制[J] . 铁道运输与经济，2004，27（3）：74-76.

[4] 程岩岩. 我国铁路乘务调度计划编制问题的研究[D] . 北京：北京交通大学，2007.

[5] 张利，刘光年，李立宏，刘征宇，张建军. 混合蚁群算法在有容量约束车辆调度中的研究[J] . 设计与研究，2007（2）：8-11.

[6] 李献忠，瑞华.于时问耗费的城市轨道交通乘务排班优化. 铁道学报. 2007，29（1）：21-25.

[7] 李继玲，卢才武，李金成. 基于蚁群算法的有时间窗车辆调度问题的研究[J] . 信息技术，2006（5）：128-131.

[8] 王芳. 蚁群算法的原理及其应用[J] . 潍坊教育学院学报.2005（2）：70-71.

[9] 黄席樾，胡小兵. 蚁群算法在K-TSP问题中的应用[J] .计算机仿真，2004，21（12）：162-164.

[10] 艾明，王魁生. 蚁群算法在TSP问题中的应用[J] . 电脑知识与技术，2006，96-129.

[11] 王世东，郑力，张智海. 蚁群算法在调机运用计划中的应用[J] . 中国铁道科学，2007，28（3）：204-209.

[12] Alberto Caprara,Matteo Fischetti,Paolo Toth,Daniele Vigo,and Pier Luigi Guida.Algorithms for railway crew management[D] . Tichnical report,DEIS,University of Bologna,Italy,DMI,Univers-ity of Udine,Italy,Ferrovie dello Stato SaA,Italy,1997.

[13] Dennis Huisman.A column generation approach for the rail crew re-scheduling problem[J] . European Journal of Operational Research, 2006.