轴线对端面的垂直度误差测量及评定*

林志熙 周景亮

(福建工程学院，福建福州350014)

检验轴线对端面垂直度的传统方法，一般将被测零件的基准面与检验平板贴合，推动宽座角尺，使宽座角尺长边工作面与被测面的母线接触，用塞尺检验母线与宽座角尺长边工作面之间的间隙，最大间隙为该母线对底工作面的垂直度误差。转动被测零件，按此法测量若干条母线对底工作面的垂直度误差，取其中最大值为该零件的垂直度误差。这种检测方法不符合GB/T 1958—2004规定的轴线对端面垂直度误差定义，只能用于检验位置精度要求较低的零件，且调整、测量效率低。

如何应用简单方便又符合国标的方法测量和评定面对线垂直度误差，一直是该研究的研究热点之一。本文采用光学分度头测量，建立基准符合最小区域法、最小二乘法的线对面垂直度误差的数学模型。按照最优化计算方法的要求，借助于MATLAB，可准确、快速地求解出基准平面度误差及面对线垂直度误差值，其结果完全符合平面度、垂直度误差的判定准则要求。

1 数学模型

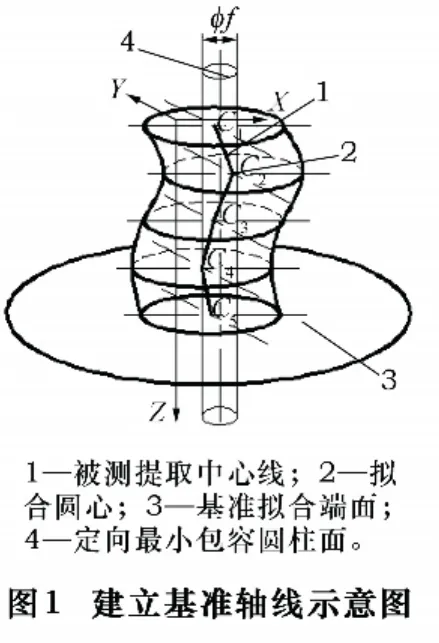
GB/T 1958—2004规定:定向最小区域是指按拟合要素的方向包容被测提取要素时，具有最小宽度f或直径Φf的包容区域［1］。在评定端面对轴线垂直度误差时，首先要确定基准要素3的方向，即对基准提取要素平面度误差进行评定。然后垂直于基准要素方向，寻找包容被测提取要素1时，具有最小直径的定向最小区域包容区域4。

1.1 建立基准平面

1.1.1 最小区域法

根据［1］规定，按最小区域法评定平面度误差实质上是寻找被测实际平面且距离最短的两平行平面。基准平面的一般方程可简写为

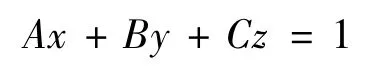
设基准面上任一测量点坐标为 Pi(xi，yi，zi)(i=1，2，…，n)，各测点到基准平面的距离为

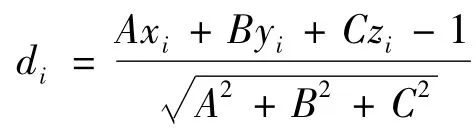
最小区域法的目标函数 F(A，B，C)=［di］max-［di］min，满足最小化时，F(A，B，C)的(A，B，C)即基准平面的法向量，且该三元函数F(A，B，C)的最小值即为平面度误差。因此基准平面的评定就转化为求三元函数F(A，B，C)的最小值问题。

1.1.2 最小二乘法

最小二乘平面是个理想平面，它使从实际被测轮廓上各点到该平面的距离的平方和为最小。因此，最小二乘法的目标函数，即各测点到最小二乘基准平面的距离的平方和，其满足最小化时，即可求得基准平面的法向量和平面度误差值。

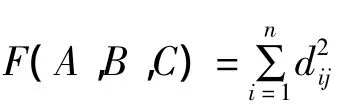
1.2 评定垂直度误差

1.2.1 最小区域圆心的确定

当对被测孔或轴的不同横截面圆进行如图1所示测量，在任一截面内做等角度采样，如图2中所示。O为分度头回转中心，即坐标原点，Δri为该截面测得的半径变化量，θi为各被测点的回转角(i=1，2，…，n)。因此测点直角坐标值xi=(r0+Δri)cosθi，yi=(r0+ Δri)sinθi。其中 r0为基圆半径(这是个未知数，但接近零件的基本尺寸)。

现采用最小区域圆法确定拟合圆心C(x，y)。各测点到拟合圆心的距离建立目标函数 F(x，y)={MAX(Ri)-MIN(Ri)}，其满足最小化时，F(x，y)的(x，y)即为各采样截面内实际轮廓的符合最小条件的拟合圆心。

1.2.2 确定被测提取轴线

图1所示被测提取中心线1就由各拟合圆心C1，C2，…，Cn连成的空间折线来体现。

1.2.3 计算垂直度误差

确定基准平面要素3的方向确定后，垂直于基准要素方向，对被测提取中心线1作最小包容圆柱面4，该圆柱面直径即为垂直度误差。

假设理想圆柱面的轴线为L，L的方向由j、k、q三参数决定，位置由u、v、g决定，则理想圆柱面的轴线可表示为

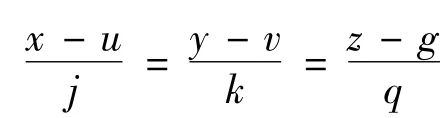
横向截面轮廓上各采样点C(xi，yi，zi)至轴线L的距离di为

其中方向向量(j，k，q)为前面作确定的基准平面的法向量(A，B，C)，参数(u，v，g)即为待优化的参数。令目标函数F(u，v，g)={max(di)}，当其满足最小化的两倍时，即为轴线对端面的垂直度误差。

2 MATLAB程序设计

Matlab 7的优化工具箱(Optimization Toolbox)中含有一系列的优化算法函数。用最小条件法、最小二乘法评定平面度误差和基准平面，测取要素的最小区域圆心，及定向最小区域包容区域的确定，均属于求解无约束条件非线性极小值。Fminsearch和Fminunc这两种函数均可。当维数不高(本文维数最多只有三维)时，只要正确建立目标函数，便有收敛速度比较快，运算结果可靠的特点［2～4］。

笔者开发的评定软件，设计了可供用户方便操作的图形用户界面［5～6］。用户可直接在界面上将所测得的数据输入到相应的文本框中，选定方法，即可得到基准要素两种评定方法的基准提取要素平面度误差以及被测提取要素垂直度误差评定结果。该软件计算精度高，直观明了，实用性强。

3 测量实例

用光学分度头对一工件进行实际测量，如图3所示。在光学分度头工作台上加装一垂直导向定位块，该定位块通过定位键与光学分度头的T形槽连接。移动杠杆千分表，从圆心开始向外每15 mm测量端面变化量，共测量3个截面，在每个截面上每转过45°由指示表在测量轮廓上测取相应的端面变化量。然后在工件圆柱上相邻15 mm截取5个截面，每个截面每转过45°测取相应的半径变化量，数据如表1所示。

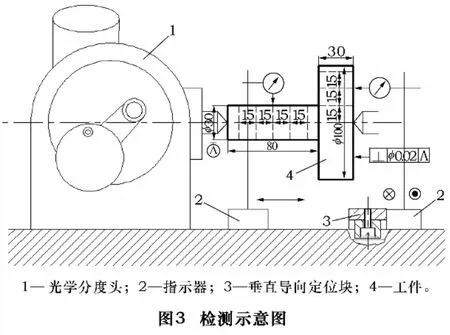
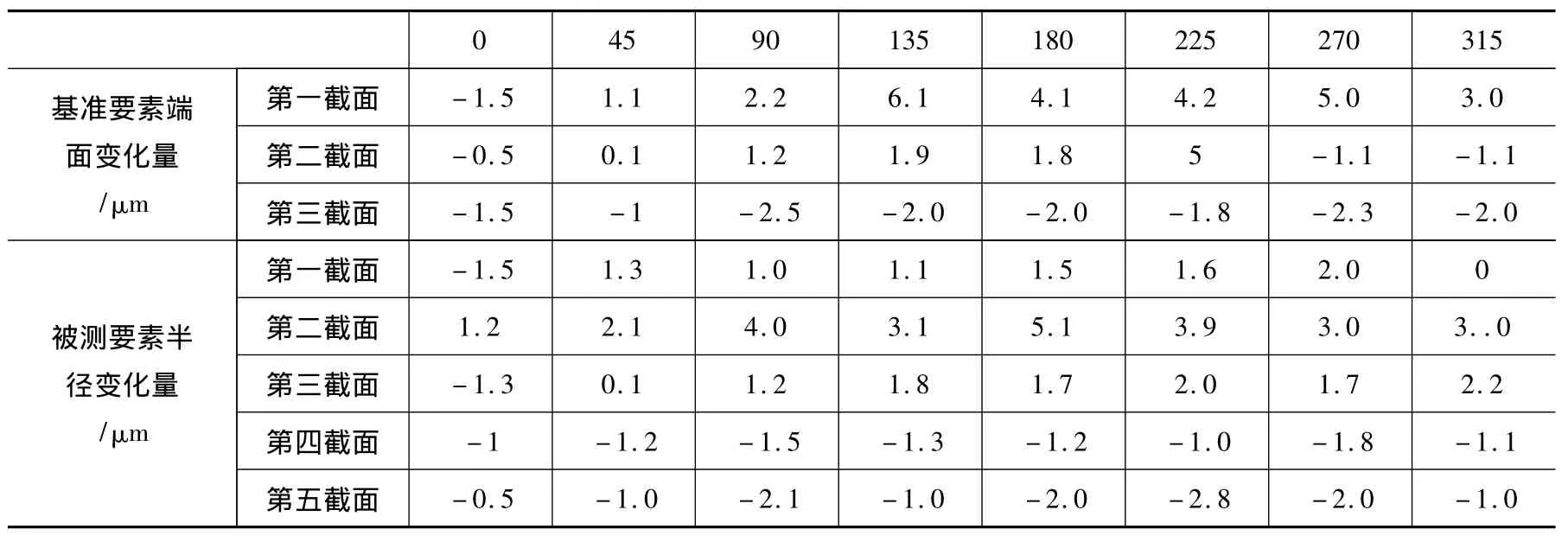
表1 测量数据

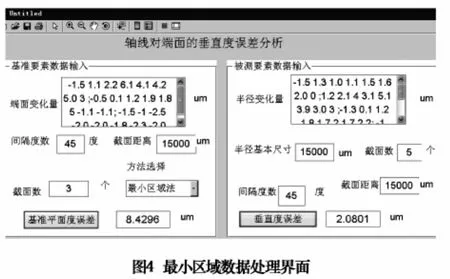
将测量数据输入系统界面，选择基准要素的评定方法，分别计算出基准要素采用最小区域法评定的平面度误差为8.4296μm，垂直度误差为2.0801μm;最小二乘法评定的平面度误差为9.0207μm，垂直度误差为1.7708μm。其中最小区域法求出的平面度误差值最小，符合国标规定。进而求出的符合定向最小区域的垂直度误差值，可作为发生争议时进行仲裁的依据。最小区域法计算界面如图4所示。

4 结语

本文研制的基准符合最小区域法、最小二乘法的线对面垂直度误差计算机数据处理系统。可同时满足基准平面度误差和轴线对端面垂直度误差的求解。通过测量实例，证明此系统的可靠性。

1 中华人民共和国国家标准GB/T 1958—2004:产品几何量技术规范(GPS)形状和位置公差检测规定.北京:中国标准出版社，2005.

2 张志涌.精通MATLAB6.5版［M］.北京:航空航天大学出版社.2003.

3 飞思科技产品开发中心编著.MATLAB 7基础与提高［M］.北京:电子工业出版社，2005(9)

4 ［美］Gerald Recktenwald著，伍卫国，方群，张辉等译.数值方法和MATLAB实现与应用［M］.北京:机械工业出版社.2002:207～229

5 王默玉，宗伟，刘春磊等.基于MATLAB的图形用户界面的构造方式与应用［J］.现代电力.2002，19(1):76 ～78

6 梁辉.MATLAB制作图形用户界面的应用［J］.佳木斯大学学报.2003，21(4):403 ～407