素数域上椭圆曲线密码体制的软件实现
金晓刚
(中国电子科技集团第30研究所,四川 成都 610041)
0 引言
椭圆曲线作为代数几何中的重要问题己有100多年的研究历史了。1985年,N.Kbolitz和V.Miler独立将椭圆曲线引入密码学[1-2],使其成为构造双密钥密码体制的一个有力工具,并形成了椭圆曲线密码体制。
椭圆曲线密码体制[3]的安全性建立在椭圆曲线离散对数问题(ECDLP)上。普遍认为其具有最高的比特安全强度。同RSA密码体制相比,要达到相同的安全强度,它可以使用较RSA密码更短的密钥。由于密钥短,所以工程实现的加密速度较快,并且可节省能源、带宽和存储空间,适于在移动通信、智能卡等系统中应用。
由于椭圆曲线密码体制具有上述优点,椭圆曲线密码体制已成为公钥密码研究的主流。
1 素数域上椭圆曲线的基本运算
1.1 群和域的概念
定义 1 设R是一个非空集合,若在R上定义一个二元运算“+”满足下列条件,称(R,+)是一个群。
①封闭性:对任何a,b∈R,有a+b∈R;
②结合律:对任何a,b,c∈R,有(a+b)+c=a+(b+c);
③交换律:存在单位元e∈R,使得对任何a∈R,有a+e=e+a=a;
④互逆性:对任何a∈R,存在逆元a-1,使得a+a-1=a-1+a=e,成立。
如R还满足对任意a,b∈R,有a+b=b+a,则称R为可交换群,或者称为阿贝尔伽群。
定义2设R是一个非空集合,在R中定义了加法和乘法两种二元运算,加法记为“+”,乘法记为“·”,如满足下列条件,称(R,+,·)是一个域。
①(R,+)是可交换群,对于加法的单位元称为零元素;
②R中的全体非零元素对乘法构成可交换群;
③乘法在加法上是可分配的,即对任何a,b,c,R∈有:
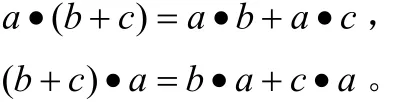
域中元素的个数称为域的阶。如果一个域的阶是有限的,则该域称为有限域。
根据有限域的定义得到下面的结论:
①如p为素数,则集合 R={0,1,2,…,p-1}是在模p加法和模p乘法下阶为p的域。由于R是由素数p构成的域,所以通常也称R为素数域,并以 G F(p)表示。如p=2,便得到素数域GF(2);
②如有一个素数p,则一定可以找到GF(p)上的一个m次既约多项式 f(x),以它为模构造出一个pm,阶的有限域GF(pm),f(x))称为域中多项式。并且该域包含了GF(p)上所有m次既约多项式的全部根,可把pm阶有限域中的每一个元素,表示成系数在GF(p)上且次数低于m的多项式。
在 G F(p)中的运算定义如下:
模p加法:a,b∈GF(p),a+b=r,r是a+b被p除得的余数,r ∈[0,p-1]。
模p乘法:a ,b∈GF(p),a·b∈s,s是a·b被p除得的余数,s ∈[0, p-1]。
求逆:若a是 G F(p)中的非零元,a的逆元 a-1就是GF(p)中的唯一元素c,且满足a·c=1。
1.2 素数域上的椭圆曲线
素数域上的椭圆曲线方程为:
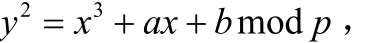
其中,素数有限域 G F(p),a、b是模p的整数,且4 a3+27 b2(modp)不等于0。
对于一个给定的椭圆曲线方程,椭圆曲线E由 G F(p)上的点(x,y)组成,其中包括一个无穷远点(ο表示)。E上点的个数(包括ο)被称作E的阶,表示成#E(G F(p ))。按照Hasse定理,阶的范围由以下公式确定:

1.3 基本运算
椭圆曲线基本运算主要是指对满足椭圆曲线方程的点(x,y)的运算,由点加运算和点乘运算(即若干次点加运算)组成。
点的加法运算有如下性质:
①加法在E上是封闭的;
②加法是可交换的;
③ο是加法的单位元;
④E上的每个点对有关于加法的逆元;
⑤加法是结合的。
因此,(E,+)是阿贝尔群。
对于一个点 P=( x,y),在素数有限域GF(p)上,其加法逆元定义为-P=( x,-y)。对于点P、Q,R =P+Q ,则P、Q、-R在一条直线上。
无穷远点ο相当于普通加法中的0,对于所有点P,有P+ο=P,P+(- P )=ο 。
(1)点加运算
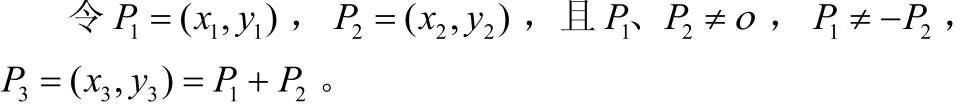
在仿射坐标系下,其运算规则如下述:
如果P1≠P2:

如果P1=P2:
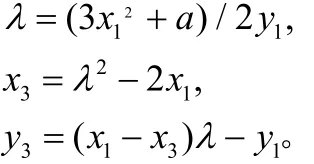
由于求逆的时间耗费远远大于乘法,为避免求逆操作,提高算法实现效率,在实际实现中,会将点对从仿射坐标系下的(x,y)转换为投影坐标系下的(X,Y,Z),其中X←x,Y←y,Z←1,在投影坐标系下进行运算。
在投影坐标系下,点加操作仅使用乘法,避免了求逆操作。仅在转换到仿射坐标系时,在点乘的最后需要一次求逆操作。求逆操作的耗费转换到多个乘法的耗费上。
(2)点乘运算
其基本描述为:Q=kP=P+P+…+P(k次),Q、P是椭圆曲线上的点,k是一个无符号正整数,1≤k≤#E(GF(p))。
点乘运算有多种实现算法,有的适合硬件实现,有的适合软件实现,算法的选择决定了实现效率。因此,应对所选择的算法进行评估,选择适合软件实现的算法。
2 素数域上椭圆曲线密码体制的软件实现
2.1 椭圆曲线密码体制
国际上,在椭圆曲线密码体制的标准化方面,IEEE、ANSI、ISO、IETF、ATM等都作了大量的工作,它们所开发的椭圆曲线标准的文档有:IEEE P1363 P1363a、ANSI X9.62、X9.63、ISO/IEC 14888等,其中包括了椭圆曲线数字签名算法ECDSA[4-6]和椭圆曲线的密钥交换协议ECDH。
为加快椭圆曲线密码体制在国内的推广,提高密码产品的安全性能,中国相关管理部门也制定了椭圆曲线密码体制的国家标准,并已颁布实施。
椭圆曲线密码体制具有相似的模块结构,如图1所示。
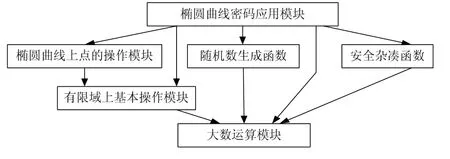
图1 椭圆曲线密码体制具有相似的模块结构
(1)大数运算模块
大数运算模块中主要包括了大数的基本操作,如大数的加、减、乘、除、平方等。
(2)有限域上基本操作模块
有限域上的操作是建立在大数操作之上的,在具体的实现过程中,需要将大数运算的结果进行取模操作,将其限制在某个大数的范围之内。
(3)椭圆曲线上点的操作模块
在实际的使用中,为了增加密码系统的安全性,用到的密码数据都是上百位的整数或二进制数。椭圆曲线密码系统当然也不例外,所以整个椭圆曲线上点的操作都是架构在已经定义与实现了的大数的操作的基础之上得。
(4)随机数生成函数模块
生成椭圆曲线密码体制需要的随机数。
(5)安全杂凑函数模块
椭圆曲线密码体制所需的安全杂凑函数。
(6)椭圆曲线密码应用模块
如密钥对生成(KG),ECDSA签名算法,ECDH算法。
2.2 软件实现
作者采用标准C语言和汇编语言相结合的方式,开发出软件包,在DSP 6205上实现了ECDSA算法,DSP主频200 MHz,带宽32比特。
ECDSA算法的密钥长度选定为192比特,采用域Fp上的椭圆曲线,其参数为 { p, a, b, G, n },以十六进制形式表示如下:

经过实际测试,ECDSA签名速率70次/秒,验证速率60次/秒。
2.3 提高软件实现效率的方法
可从以下几个方面提高椭圆曲线密码算法的实现效率:
①对点乘运算模块、大数运算模块,选择最适合软件实现的算法;
②模乘运算是椭圆曲线密码算法最基本的算法模块,进行一次签名运算,调用次数上千次。可从两方面加快模乘运算:汇编实现 Montgomery乘法,尽量提高编程效率;用硬件协处理器完成模乘运算;
③采用运算能力较强的处理器,如DSP6205,其带宽32比特,内核时钟 200 M,编译器效率高,能够很好的实现椭圆曲线密码算法;
④椭圆曲线密码算法在签名和加密时,需要输入随机数。因此,随机数的生成时间尽可能短。
3 结语
目前,国际上公认的比较安全实用的公钥密码体制是椭圆曲线密码体制。经过长期的理论研究和科学实践,椭圆曲线密码体制得到了迅猛的发展。椭圆曲线密码体制的安全性,是基于计算有限域上椭圆曲线可交换群群上定义的离散对数的困难性。椭圆曲线密码体制具有安全性能高、存储空间占用小和带宽要求低等特点,在如 PDA、手机、智能卡等领域具有很大的发展优势。现在椭圆曲线密码体制不仅是一个重要的理论研究领域,而且已经从理论研究转化为实际可用的密码算法,促使民用信息安全技术走向产业化。当前,国内外很多生产密码产品的公司都在致力于椭圆曲线密码体制产品的开发。
现所做的主要工作有:
①对椭圆曲线密码体制的基础理论知识进行了简单介绍;
②介绍了椭圆曲线密码算法层次结构;
③讨论了素数域上椭圆曲线密码体制的软件实现,给出了提高算法实现效率的一些方法。
由于椭圆曲线密码体制自身优越条件,它将会成为 21世纪最主要的公钥密码体制。按当前的电子信息化程度,椭圆曲线密码体制将会迅速扩展到人们生活的各个层面,具有广阔的应用前景。
[1] 卢开澄.计算机密码学[M].北京:清华大学出版社,2001.
[2] BRUCE S.应用密码学[M].北京:机械工业出版社,2002.
[3] KOBLITZ N. Elliptic Curve Cryptosystems[J].Mathematics of Computation,1987(48):203-209.
[4] FIPS PUB 186. Digital Signature Standard[EB/OL] (2009-06-01)[2010-07-30].http://www.itl.nist.gov/ fipspubs/.
[5] DON J,ALFRED M,SCOTT V.The Elliptic Curve Digital Signature Algorithm[J].International Journal of Information Security,2007,1(01):36-63..
[6] IEEE P1363/D9(Draft Version 9).Standard Specification for Public Key Cryptography[EB/OL](2008-10-10)[2010-07-30].http://grouper.ieee.Org/ groups/1363.
[7] DARREL H, ALFRED M,SCOTT V.椭圆曲线密码学导论[M].北京:电子工业出版社,2005.
[8] MICHAEL W.密码编码学-加密方法的C与C++实现[M].第2版.北京:电子工业出版社,2003.

