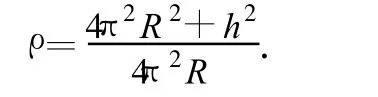用物理方法求曲线运动的曲率半径

黄振平

(江苏省靖江高级中学,江苏靖江 214500)

2008年江苏高考物理题中出现了摆线的曲线半径,在运用动力学方法推导开普勒第二定律中远地点、近地点速度关系时也要用到曲率半径,而曲率半径在数学上有严格的意义和表达式.在中学阶段,也可用物理方法求运动轨道的曲率半径,下面给出几种典型曲线运动的曲率半径.

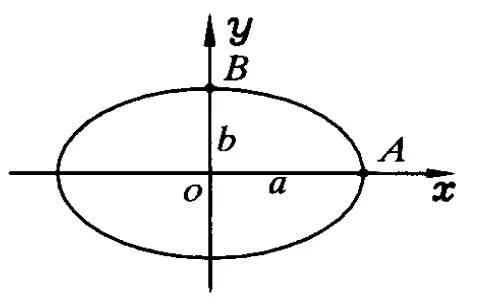
图1

解析:如图 1,把质点的椭圆运动看成两个互相垂直的同频率简谐运动的叠加.设质点的运动方程为

对应的轨道方程就是题中给出的椭圆方程.

A(a,0)的速度vA是切向速度,又是质点在y方向振动时的速度振幅,有

此处质点受力沿x方向,即曲线的法向,大小为

法向加速度为

由(3)式和(5)式得到 A(a,0)处曲率半径为

同理求得B(0,b)处切向速度、法向加速度、曲率半径分别为

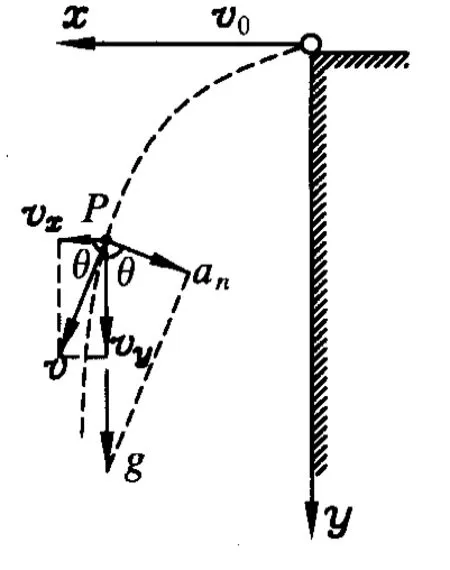
图2

例2.如图 2,一物体作初速为v0的平抛运动,得到一抛物线轨迹,求在抛物线上任一点处的曲率半径.

解析:图2中的抛物线方程可写为

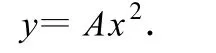
抛体的运动方程为

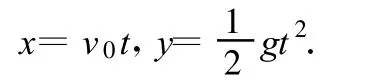
消去t得轨道方程

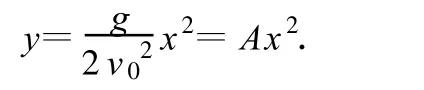
所以

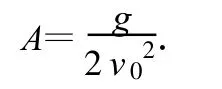
设 t时刻抛射体抵达P点,其坐标为(x,y).为得到此处曲率半径ρ,可利用图中速率v和法向加速度an求得.

因为 vx=v0,vy=gt,所以又 an=得到

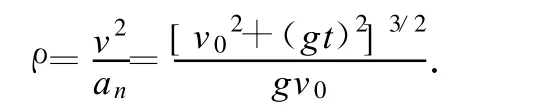
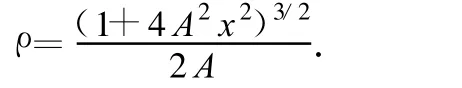
例3.一个刚性圆轮在直线轨道上作纯滚动,圆轮边缘上一点所经历的轨迹称为滚线(又称旋轮线、摆线).所谓纯滚动就是圆轮与直线轨道的接触点无相对运动.设圆轮半径为R.试求滚线上各点的曲率半径.

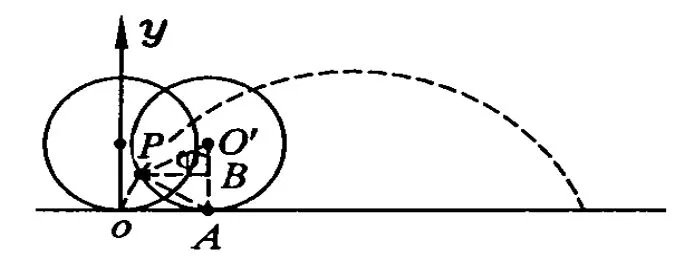
图3

解析:滚线形状与圆轮滚动快慢无关.选定一种圆轮滚动的方式,圆心O′以不变的速度v0沿直线轨道向右运动,同时圆轮绕圆心 O′以不变的角速度ω转动,为保证圆轮在直线轨道上作纯滚动,应有关系式

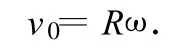
设圆轮滚动φ角,P点达图3所示位置,P点瞬时速度为

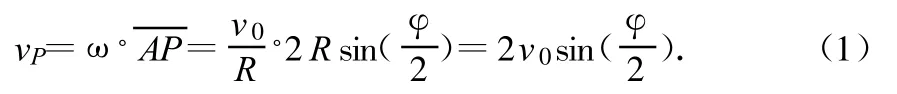
其方向必沿滚线在P点的切线方向.P点的加速度为

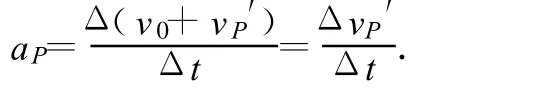
此处已利用 v0是常量,轮心作匀速运动.vP′是P点相对O′的相对速度.此式说明,由于牵连加速度为零,绝对加速度等于相对加速度.故有

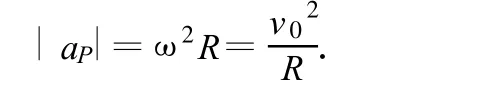
方向由P指向O′.因此,P点的法向加速度为

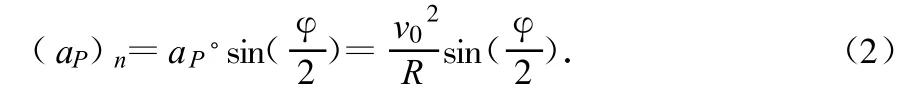
这里P点处曲线的法向为AP方向.由(1)、(2)式,得 P点曲率半径为

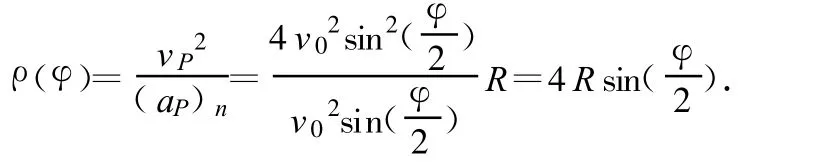
这就是各φ处曲线的曲率半径.

例4.一杂技演员在圆筒建筑物内壁表演飞车走壁.演员骑摩托车从底部开始运动,随着速度增加,圈子越来越大,最后进入圆筒形直壁上行驶.开始在直壁上同一高度内作圆周运动,继而又在直壁上作等距螺旋运动.已知圆筒直壁的半径为 R,摩托车行驶速率为 v(匀速率运动),演员和摩托车的总质量为M.求:摩托车在圆筒形内壁上作等距螺旋线运动时螺旋轨道的曲率半径[如图4(a),设螺距为h].

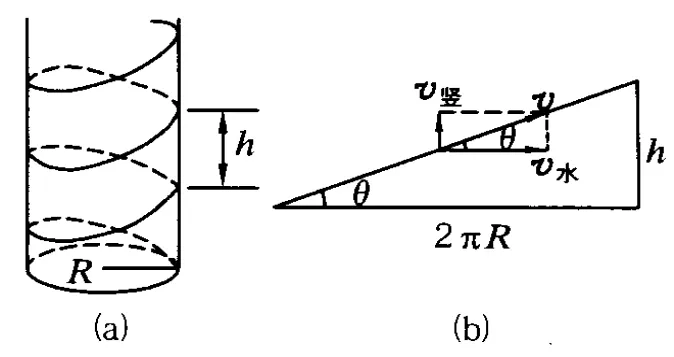
图4

解析:摩托车作等距螺旋运动时,由于速率v不变,无切向加速度.设摩托车的速度分解成水平方向速度 v水和竖起方向速度v竖,由于摩托车作等距螺旋运动,且运动中速率不变,所以可以知道,v竖在运动中方向和大小均保持不变;v水在运动中大小不变,方向不断变化,其运动相当于同一水平面内作半径为 R的匀速圆周运动.则

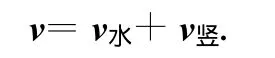
摩托车的加速度为

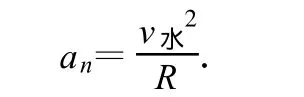
从摩托车运动的角度写出法向加速度.尽管螺旋线是一条三维空间的曲线,但可以用与二维平面曲线确定曲率半径相类似的原则来确定螺旋线的曲率半径.因为在三维曲线上取一小线元,当线元趋于零时,必将趋于同一平面上的小圆弧,对应的圆弧半径就是在该处的曲率半径.由此可以写出法向加速度.因等距螺旋线的对称性,各处的曲率半径相同,设为ρ,摩托车作螺旋运动时的法向加速度可以写为

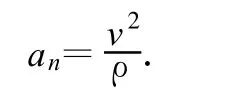
两式比较得

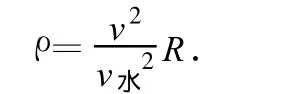
利用摩托车在筒壁绕一圈的几何关系,如图4(b),得到

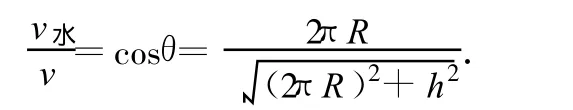
代入ρ的表达式,得螺旋线曲率半径为