构建与解读“星体”模型

俞丽萍

(浙江上虞春晖中学,浙江上虞 312353)

1 构建

作用特征:两个物体在相互间力的作用下,绕着某一点做匀速圆周运动.

遵循规律:①两个物体做匀速圆周运动的角速度ω相同、周期 T相同.

②两个物体做匀速圆周运动的半径与物体的质量成反比,若物体的质量分别为 m1、m2,物体的运动半径分别为r1、r2,则 Fn=m1ω2r1=m2ω2r2,所以得到 m1r1=m2r2.

2 解读

2.1 从“双人”到“双星”

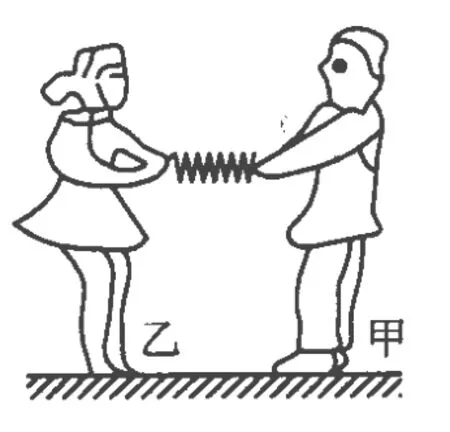
图1

例1.甲、乙两名溜冰运动员,面对面拉着弹簧秤做圆周运动的溜冰表演,如图 1所示.已知 M甲=80 kg,M乙=40 kg,两人相距0.9 m,弹簧秤的示数为96 N,下列判断正确的是

(A)两人的线速相同,约为40 m/s.

(B)两人的角速相同,约为2 rad/s.

(C)两人运动半径相同,都为0.45 m.

(D)两人运动半径不同,甲为0.3 m,乙为0.6 m.

解析:甲、乙两运动员在相互间拉力的作用下做匀速圆周运动,拉力提供向心力,由 M甲r甲=M乙r乙,r甲+r乙=0.9 m,可求得 r甲=0.3 m,r乙=0.6 m.Fn=M甲ω2r甲=M乙ω2r乙,解得 ω=2 rad/s,故此题选(B)、(D).

例2.(2008年宁夏卷)天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可推算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为 T,两颗恒星之间的距离为 r,试推算这个双星系统的总质量.(引力常量为G)

解析:设两颗恒星的质量分别为 m1、m2,做圆周运动的半径分别为 r1、r2,角速度分别为 ω1,ω2.根据题意有

根据万有引力定律和牛顿定律,有

联立以上各式解得

根据角速度与周期的关系知

联立(3)、(5)、(6)式解得

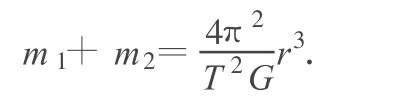
点评:在“双人”模型中,若将两运动员看成是两颗恒星,将两运动员之间的拉力看成是万有引力,那么,对于“双星”模型的理解也就不难了.

2.2 从“双星”到“双电荷”

图2

例3.如图2所示,两个正、负点电荷,在库仑力作用下,它们以两者连线上的某点为圆心,做匀速圆周运动,以下说法正确的是

(A)它们所需的向心力大小不相等.

(B)它们做匀速圆周运动的角速度相等.

(C)它们的线速度与其质量成反比.

(D)它们运动半径与电量成反比.

解析:两个正、负点电荷,以两者连线上的某点为圆心做匀速圆周运动,库仑力提供向心力,两个点电荷构成双星模型,故两者向心力的大小相等,角速度相等,又由于m1r1=m2r2,所以 m1ω r1=m2ω r2,m1v1=m2v2, 故此题选(B)、(C).

2.3 从“双星”到“三星”

例4.(2006年广东卷)宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为 R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行.设每个星体的质量均为 m.

(1)试求第1种形式下,星体运动的线速度和周期.

(2)假设两种形式星体的运动周期相同,第2种形式下星体之间的距离应为多少?

解析:第1种形式下,由万有引力定律和牛顿第二定律,得

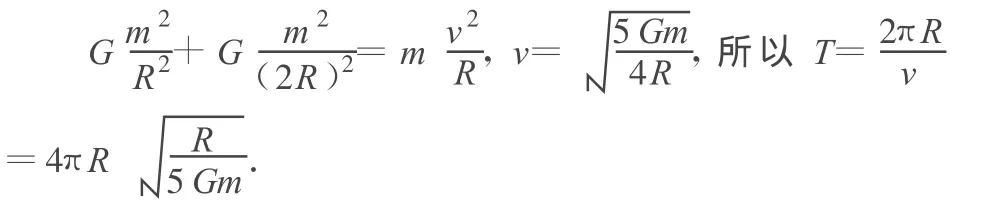
第2种形式下,由万有引力定律和牛顿第二定律,得

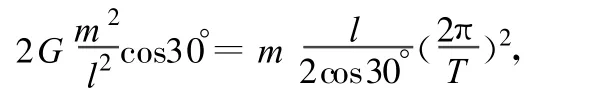
2.4 从“三星”到“四星”

例5.宇宙中存在一些离其他恒星很远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用,稳定的四星系统存在两种基本的构成形式:一种形式是四颗质量相等的星位于正方形的四个顶点上,沿外接于正方形的圆形轨道运行:另一种形式是四颗质量不等的星位于同一直线上,间距相等,均围绕中点做圆周运动,已知第一种形式中每颗星质量均为m,正方形边长为a,求它们的运行周期T.

解析:已知第一种形式中每颗星质量均为m,正方形边长为a,每颗星体在其他三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,由万有引力定律和向心力公式得

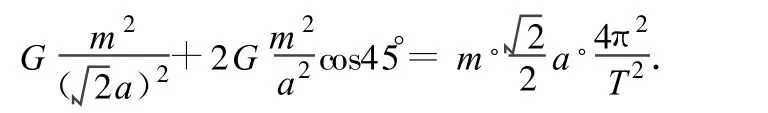
解得周期

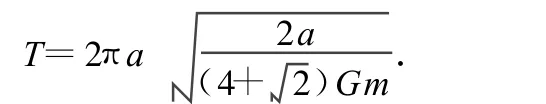
点评:从数量而言,双星、三星、四星星体数量逐渐增加,而且“三星”与“四星”都出现了两种不同的稳定形式,但无论是哪一种形式,对研究对象进行受力情况分析,找出向心力的来源是解决问题的关键所在.

2.5 从“双星”到“暗星”

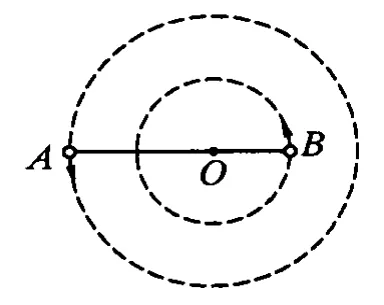
图3

例6.(2006年天津卷)神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图3所示.引力常量为 G,由观测能够得到可见星 A的速率v和运行周期T.

(1)可见星 A所受暗星B的引力FA可等效为位于O点处质量为m′的星体(视为质点)对它的引力,设 A和B的质量分别为m1、m2,试求 m′(用 m1、m2表示);

(2)求暗星 B的质量m2与可见星 A的速率v、运行周期T和质量m1之间的关系式;

(3)恒星演化到末期,如果其质量大于太阳质量 ms的2倍,它将有可能成为黑洞.若可见星 A的速率v=2.7×105m/s,运行周期 T=4.7π×104s,质量 m1=6ms,试通过估算来判断暗星B有可能是黑洞吗?

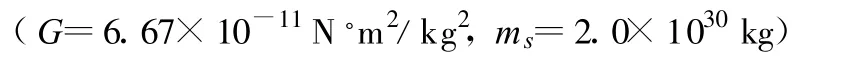
解析:(1)设 A、B的圆轨道半径分别为r1、r2,由题意知,A、B做匀速圆周运动的角速度相同,设其为ω.由牛顿运动定律,有

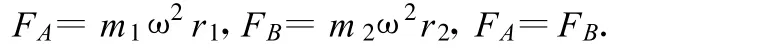
设 A、B之间的距离为r,又 r=r1+r2,由上述各式得

由万有引力定律可得

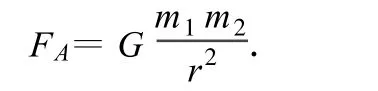
将(1)式代入得

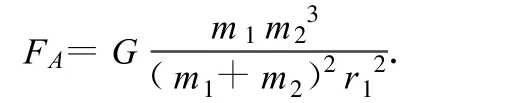
(2)由牛顿第二定律,有

又因为可见星 A的轨道半径

由(2)～(4)式解得

(3)将 m1=6ms代入(5)式,得

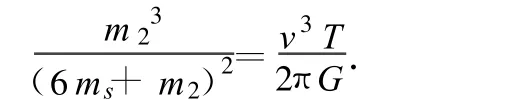
代入数据得

m2=nms(n＞0),将其代入(6)式得

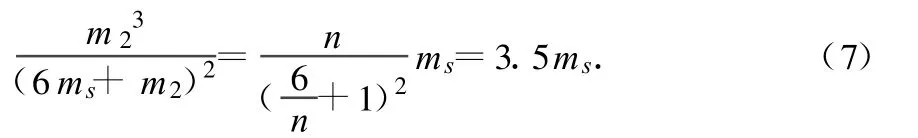
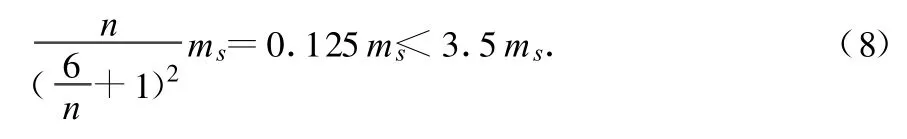
若使(7)式成立,则 n必大于2,即暗星B的质量 m2必大于2ms,由此得出结论:暗星B有可能是黑洞.

点评:利用双星系统的运动规律可以来研究不可见的暗星B的等效质量m′,进而探讨暗星B是否有可能是黑洞.

无论是双星还是多星,处理“星体”模型的关键是通过对研究对象的受力分析明确向心力的来源,通过几何关系确定圆周运动的半径,再利用圆周运动的运动规律展开讨论.