弹簧振子问题综述

谭 永 杨宇红

(湖北省武汉市武汉中学,湖北武汉 430060)

若物体与弹簧相连,弹簧的另一端固定,不计物体受到的摩擦或空气阻力,弹簧的质量比物体小得多,可以略去不计,这样的系统叫弹簧振子,这个物体叫振子,弹簧振子有以下几种放置方式(如图1).

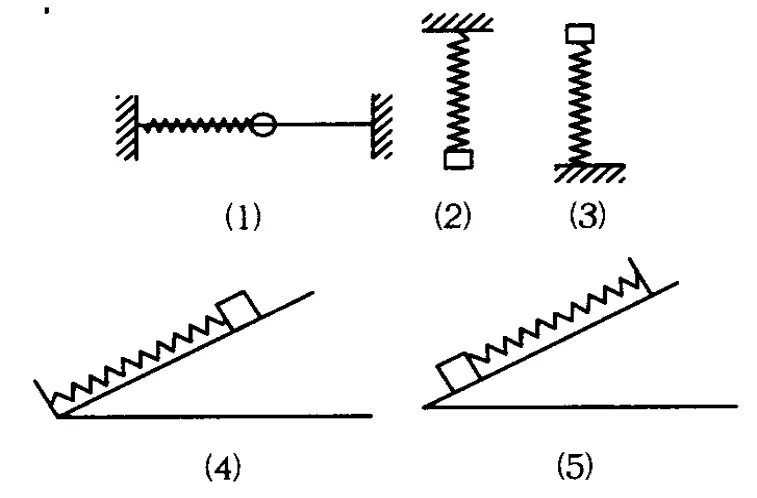
图1

弹簧振子的特点有:

(1)振子沿弹簧轴线方向的自由振动为简谐运动,遵守F回=-kx(其中 k为弹簧的劲度系数).

(3)弹簧沿弹簧轴线方向简谐运动时 F回max=kA,其中 m为弹簧振子质量).

对多个物体组成的系统弹簧振子的判断是个难点,例以图2中若不计一切摩擦,且弹簧为轻弹簧,A和B、C和D、E和F沿弹簧轴线运动,且始终不分离,则做简谐运动的是______,可称为弹簧振子的是_____.

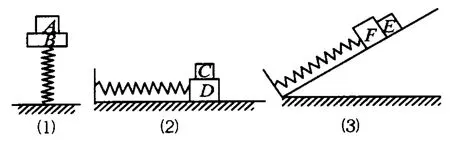
图2

解析:将 A和B、C和D、E和F视为一个整体,它们均做简谐运动,故 A、B、C、D、E、F 均做简谐运动,A和B、C和D、E和F与弹簧组成的整体符合弹簧振子的定义,叫弹簧振子.

答案:A、B、C、D、E、F;A和B及弹簧、C和D 及弹簧、E和F及弹簧.

关于弹簧振子的主要题型如下.

1 利用简谐运动的对称性解题

例1.如图3所示,一轻质弹簧与质量为 m的物体组成弹簧振子,物体在一条竖直线上的 A、B间做简谐运动,O为平衡位置,C为AO的中点,已知 OC=h,振子的周期为 T,某时刻物体恰好经过 C点并向上运动.则此时刻开始的半个周期内正确的是

(A)重力做功 2mgh.

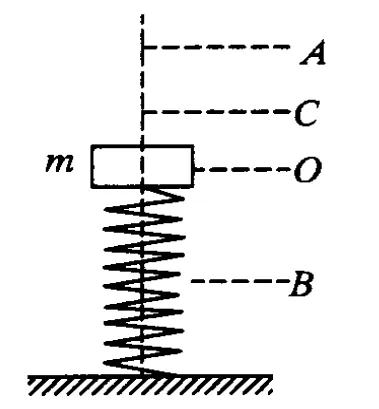
图3

(C)回复力做功为0.

(D)回复力冲量为 0.

解析:做简谐运动的物体在间隔半周期奇数倍的两个时刻的位置关于平衡位置对称,且这两个时刻所有矢量等大反向.所以半周期时刻振子一定在平衡位置下方 C′处.OC′=OC=h,且速度大小与 C点等大反向,故(A)对;重力为恒力,故(B)对;回复力的功即合力的功为 0,故(C)对,而 I回=ΔP=mVC′-m(-VC′)≠0.所以答案为(A)、(B)、(C).

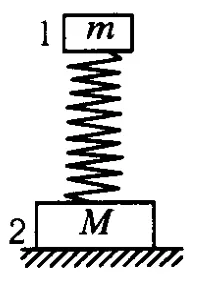
图4

例2.如图4所示,两木块质量分别为 m和M,用劲度系数为k的轻质弹簧连在一起,竖直放置在水平面上,将木块1压下一段距离后由静止释放,它就上下振动,在振动过程中木块2刚好始终不离开地面(即它对地面的最小压力为零),求:(1)木块1的最大加速度;(2)木块2对地面的最大压力.

解析:木块2刚好不离开地面即木块1在最高点时,M受地面支撑力为零.

(1)木块1在最高点时,由木块2的平衡知此时 F弹=Mg,此时木块 1在最高点,具有最大加速度,amax=方向向下.

(2)木块1在最低点时,向上回复力最大,弹力最大,弹簧对2的向下弹力最大,木块2对地面有最大压力.由对称性知木块 1在最低点,得F弹′=Mg+2mg,方向向上.由木块2的平衡知地面对木块2的弹力为N=2(M+m)g.

2 两物体组成的系统临界值或范围值的求解

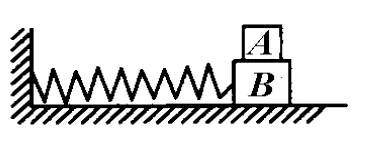
图5

例3.(2006年福建福州质量检测)如图5所示,质量为 m的物体A放在质量为M的物体B上,B与弹簧相连,它们一起在光滑的水平面上做简谐运动.振动过程中 A、B之间无相对运动,设弹簧的劲度系数为 k,振动的幅度为 A0,重力加速度为 g,则物体A、B间动摩擦因素μ的大小范围是________.

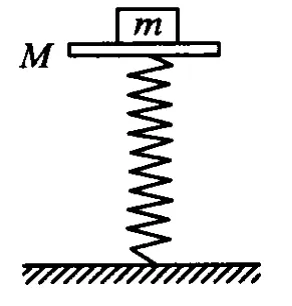
图6

例4.如图6所示,一个竖直弹簧连着一个质量为 M的薄板,板上放着一木块,木块质量为m.现使整个装置在竖直方向上作简谐运动,弹簧的劲度系数为k,若要求整个过程中小木块 m都不脱离薄木板,系统振幅不能超过多少?

3 简谐运动的变化分析

简谐运动物体振幅是振动物体离开平衡位置的最大距离,也是速度由最大处运动到速度为0处的距离.振幅由系统机械能决定,质量一定的做简谐振动的物体,机械能越大,振幅越大;若振子质量改变,则不一定能由机械能情况推断振幅变化.

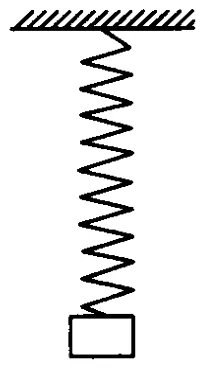
图7

例5.如图7所示,竖直悬挂的弹簧振子作振幅为 A的简谐运动.当物体到达下面最大位移时,恰好物体掉了一半(即物体质量减少了一半),此后振动系统的振幅的变化为

(A)振幅不变. (B)振幅变大.

(C)振幅变小. (D)条件不够,不能确定.

解析:质量改变前后,最低点位置不变,但质量减少一半后的平衡位置会升高,即最低点到平衡位置的距离变大,故振幅会变大.

例 6.如图8所示,质量为 M的物体拴在水平放置的左端固定的轻弹簧右端,构成一弹簧振子.物体可在光滑水平面上做简谐运动,振幅为 A.在运动过程中,将一质量为m的小物块轻放在M上,第1次是当 M运动到平衡位置时放在上面,第2次是当 M运动到最大位移时放在上面.观察到第1次放后的振幅为 A1,第2次放后的振幅为 A2,则

(A)A1=A2=A. (B)A1＜A2=A.

(C)A1=A2＜A. (D)A2＜A1=A.

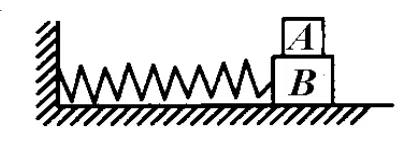
图8

解析:当 M在最大位移处放上m,则放上m前后最大位移位置和平衡位置均不变,振幅不变.若在平衡位置放上m,M、m会相对滑动产热,系统最大动能变小,最大弹性势能会变小,从而弹簧最大形变即振幅会变小.答案应选(B).

4 弹簧振子能量问题

弹簧振子在做简谐运动时,系统的机械能守恒.即动能+弹簧势能+重力势能=定值,由其中一种(或两种)能量的变化,可推断其他能量的变化.

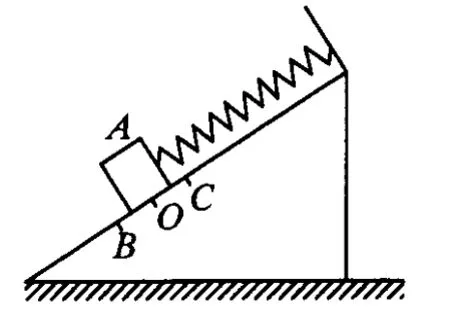
图9

例7.光滑斜面上物块 A被平行斜面的轻质弹簧拉住静止于O点,如图9所示,现将 A沿斜面拉到B点无初速度释放.物体在BC范围内做简谐运动,则下列说法正确的是

(A)OB越长,振动能量越大.

(B)在振动过程中,物体 A机械能守恒.

(C)A在C点时,物体与弹簧构成的系统势能最大,在O点时势能最小.

(D)A在C点时,物体与弹簧构成的系统势能最大,在B点时势能最小.

解析:对质量一定的弹簧振子,振幅越大,振动总能量越大,(A)对;振动过程中,A与弹簧组成的系统机械能守恒,势能为重力势能和弹簧势能之和,势能最大时应为动能最小时,(C)对.笞案:(A)、(C).

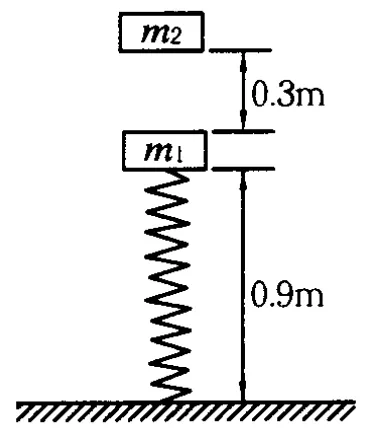
图10

例8.如图 10所示,一轻质弹簧竖直固定在地面上,自然长度为1 m,上面连接一个质量为 m1=1 kg的物体,平衡时物体离地面0.9 m.距物体的正上方高为0.3 m处有一个质量为 m2=1 kg的物体自由下落后与弹簧上物体 m1碰撞后即合为一体,一起在竖直面内做简谐运动.当弹簧压缩量最大时,弹簧长为0.6 m(g取10 m/s2),求:(1)碰撞结束后瞬间物体的动能之和;(2)两物体一起做简谐运动时振幅;(3)弹簧长为0.6 m时,弹簧的弹性势能.

解析:(1)m1与 m2接触时,由得

m2与 m1碰撞由动量守恒,则 m2v0=(m1+m2)v,v

(2)m2与m1平衡时压缩量=m1平衡时压缩量的2倍=2×0.1 m=0.2 m,即弹簧长度0.8 m处,而最低点弹簧长度0.6 m,所以 A=0.2 m.

(3)由简谐运动对称性知,m1和 m2简谐运动最高点是弹簧处于原长状态处,从最低点到最高点,由机械能守恒可知,Ep′=(m1+m2)gh=8 J.(收稿日期:2009-10-25)