战时维修力量最大覆盖选址问题
李 明,曲长征, 张 波,高 飞 (军械工程学院,河北 石家庄 050003)
0 引 言
选址问题在生产、生活、物流、军事中都有非常广泛的应用,因而,从上世纪六七十年代起,该问题就已开始被较系统地研究[1]。Brandeau等在对选址问题的综述中将选址问题归纳为50多类,并指出了各类问题相互之间的关系[2]。选址研究中的一些典型问题,如Weber问题、p-中值问题、覆盖问题、p-中心问题、多目标选址、竞争选址、不受欢迎的设施选址、选址—分配、选址—路线等,都是引起广泛关注和深入研究的热点课题[3]。覆盖问题主要有两类基本模型:集合覆盖模型 (the Set Covering Location Problem,SCLP)和最大覆盖模型 (the Maximal Covering Location Problem,MCLP)。最初的MCLP问题是由Church和ReVelle提出的,即先固定设施数目,再确定它们的位置使得其覆盖尽可能多的需求点或需求量[4]。维修力量的配置包括维修机构的配置和维修人员的配备。维修机构配置位置的合理与否直接关系着维修系统能否在可用的时间范围内为作战单位提供维修服务、所提供服务的效率高低、以及设施建设和运行成本等一系列问题,直接影响着系统对维修需求的反应能力[5]。本文尝试用最大覆盖选址模型解决该问题。
由于任务的紧急程度、作战要求各不相同,各个作战区域内作战单位对接受维修服务的优先程度也各不一样,而传统的MCLP模型并没有充分考虑这一因素对选址的影响。本文主要针对维修机构的选址问题进行研究,建立了以作战区域内所有需求点优先度和值最大为目标的有限服务台优化模型。
该模型是在传统网络覆盖问题的基础上,借鉴 “部分覆盖”[6]的思想,建立的一种适用于军队战时的覆盖问题模型,扩展了覆盖问题的应用范围。
1 模型的建立
1.1 优先度函数
高技术条件下作战,装备保障必须坚持 “一切为了前线,一切为了胜利”的总方针,而 “统筹兼顾,保障重点”是战时装备保障必须遵循的基本原则之一。装备保障的重点通常是指,影响合成指挥员决定实现,与战斗全局胜负相关的战斗行动和单位[7]。
设 ci、 ri分别是第 i( i=1,2,…,n )个需求点的优先权和需求量,lij为需求点i到备选服务台j( j=1,2,…,m )的最短距离, 同时引入相对距离的概念,记为我们将需求点的优先权从高到低依次划分为一、二、三三个等级,其对应的ci则分别被赋以5、3、1三个值。ki为需求点i的时间敏感性参数,用以表示需求点i对保障时间的敏感程度,0<ki≤1。f(ci, ri,lij)为第j个备选服务台对第i个需求点的优先度函数。
基于以上各因子,第j个备选服务台对第i 个需求点的优先度函数可表示为:

1.2 基于需求点优先度的最大覆盖模型
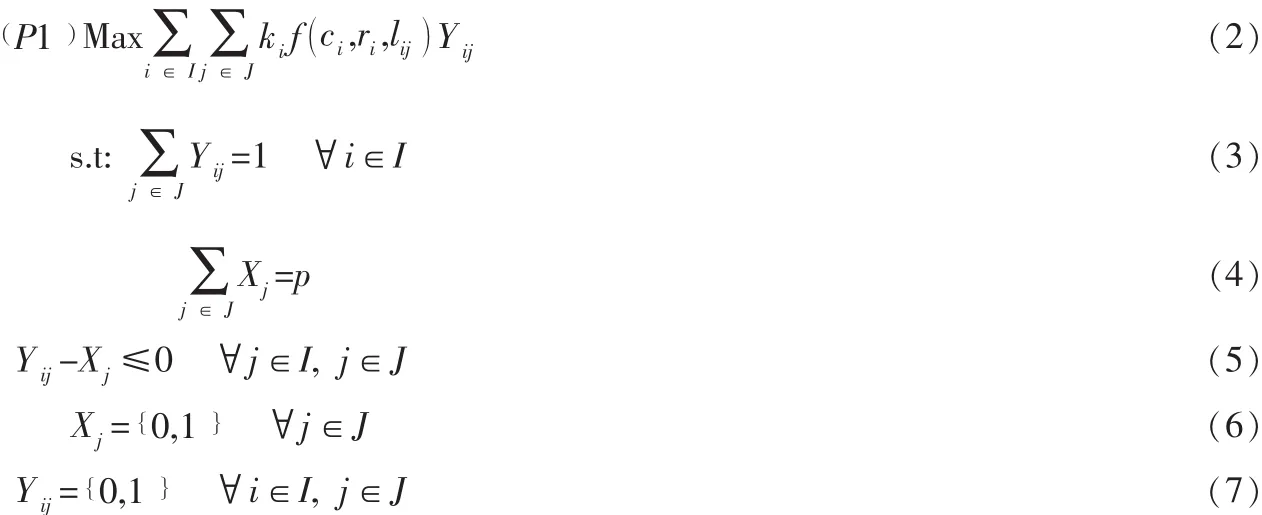
其中优先度函数f( ci, ri,lij)可由式 (1)给出;Xj取值为1时表示在候选点j处设立服务台,否则取值为0;Yij取值为1时表示需求点i的顾客接受设在j处服务台的服务,否则取值为0。
该模型的目标函数式 (2)表示是总的优先度最大;约束式 (3)是保证每个需求点只被一个服务台 (对该需求点优先度最大的服务台)服务;约束式 (4)是保证建立的服务台数量为p个;约束式 (5)是根据某备选址点是否设立服务台而对需求点优先度的限制,如果某服务台没有设立,则所有接受该服务台服务的需求点的优先度都将变成0;约束式 (6)、 (7)是对所有决策变量的0、1约束。
在上述模型中,还有一个假设的前提,即所有的需求点都被覆盖,只不过被覆盖的程度按需求点的优先度来区分。
2 算 法
最大覆盖选址问题是NP困难问题,目前关于解决此类问题的算法已经很多,常用的有贪婪算法、禁忌搜索算法、模拟退火算法、拉格朗日松弛算法、蚁群算法等。本文尝试用拉格朗日松弛算法解决该问题。拉格朗日算法的基本原理是,将造成问题难的约束吸收到目标函数中去,并使得目标函数仍保持线性,通过对松弛过程的控制,可以得到问题的最优解或知道所得到的解距离最优解的最大差距是多少[8-9]。
对于P1问题,首先将约束式(3)松弛到目标函数(2)中去,并规定对应于约束式(3)的拉格朗日乘子λi≥0 i∈()I。由此得到本文模型的拉格朗日松弛问题 (记为P2)
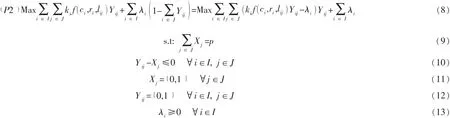
式 (8)中λi为拉格朗日乘子,对于固定的λi,式 (8)中后半部即为常量,因此,为使问题P2的目标函数式 (8)最大化,我们将 (8)最大化,我们将Yij进一步定义为:



对于确定的拉格朗日乘子来说,Vj的值也是确定的,因此可以通过寻找p个最大的Vj的办法求得问题P3的最优解,并将相应的Xj设为1,其余的Xj设为0,再由式 (14)求出Yij的值,进而得到问题P2的最优解,记为ZU。
由于没有考虑到原模型中约束式 (3)的限制,此时问题P2的最优解并不一定是原问题的解。但是就任一需求点i而言,可以在P3最优解确定的选址点中找到一个使其优先度最大的服务台,得出原问题的一组可行解。该可行解为原问题求解提供了目标函数的下限ZL:
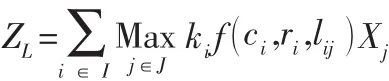
通过调整拉格朗日乘子,可以使问题目标函数的上下限不断逼近求解该问题。本文利用次梯度算法来逼近最优解[8]。若用k表示迭代次数,则第k次迭代的最优值上下限分别表示为和,相应的拉格朗日乘子为,拉格朗日松弛问题P2的最优解为和用tk表示第k步的步长,ZLB为第k次迭代为止最大的下限值,αk是第k次迭代步长参数(0<αk≤2 )。
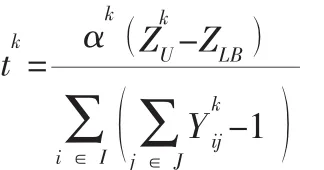
再设ZUB为第k次迭代为止最小的上限值。则基于拉格朗日松弛算法的步骤如下:
第一步: 初始化模型参数, 令ZLB=-∞,ZUB=+∞,k=0,=0(∀i∈I ), αk=2;
第四步:更新原问题的上下限。若
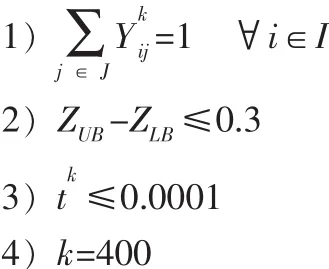
第七步:更新拉格朗日乘子,转到第二步。
3 结 论
在战时,保障系统的快速反应能力对战争的胜负起着至关重要的作用,而保障设施的选址对保障系统的快速反应能力具有根本性的影响。本文以需求点优先度函数作为目标函数,并基于拉格朗日松弛算法给出了该模型的启发式求解方法。该模型可用于战时定点维修机构的选址决策。保障设施选址问题还有很多方面值得进一步研究,如随机需求的选址问题、多阶段任务条件下的动态设施选址问题等,将是以后研究的重点。
第五步:检验步长更新条件,更新步长参数αk。若上限ZUB在连续4次迭代都没有变化,则令αk=αk/2;
第六步:检验迭代结束条件,如果以下条件中任何一个满足,终止迭代求解过程:
[1] Marianov V,Re Velle C.Siting emergency services.In:Drezner Z,editor.Facility location[M].Berlin:Springer,1995:199-223.
[2] Brandeau ML,Chui SS.An overview of representative problems in location research[J].Management Science,1989,35(6):645-674.
[3] 卜月华.图论及其应用[M].南京:东南大学出版社,2000.
[4] Church RL,Re Velle C.The maximal covering location problem[J].Papers of Regional Science Association,1974,32:101-118.
[5] 龚延成.战时军事物流系统决策理论与方法研究[D].西安:长安大学 (博士学位论文),2004.
[6] Berman O.The p maximal cover-p partial center problem on the networks[J].European Journal of Operation Research,1994,72:432-442.
[7] 孔令茂,等.战术装备保障学[M].北京:国防大学出版社,2002.
[8] 刑文训,谢金星.现代优化计算方法[M].北京:清华大学出版社,2005.
[9] 王文峰.装备保障网络优化设计问题研究[D].北京:国防科技大学 (博士学位论文),2008.

