基于客户满意度的服装业车辆调度研究
孙琼玲, 王 亮 (南京财经大学,江苏 南京 210046)
0 引 言
20世纪60年代,欧美学术界就已提出 “服务中心”理论,该理论主要观点是企业进行物流管理和决策不能仅仅强调节约消耗,降低成本,而应该立足于在保持和提高企业对客户的服务水平的基础上,通过寻求物流成本与服务之间的平衡点,保持企业的竞争优势。
在服装业这个时效性很强的行业里,若配送不能在零售商要求的时间内到达,会造成产品脱销,给零售商造成利润损失,从而降低客户满意度。配送到达时间的准时与否,已成为客户衡量配送服务水平的高低。准确的到达时间需要配送中心合理的车辆调度方案,这就要求企业从客户的角度去考虑问题。
据罗兰·贝格与中国连锁经营协会在2003年对国内多个连锁零售企业调查结果显示:其缺货问题是配送中的重要症结,每年因缺货导致损失近四成消费机会。与生产企业不同,服装门店多分布在商业区,竞争激烈,顾客停留时间短,缺货时顾客等待可能性小,给零售商造成损失,在销售旺季节,损失会更严重。
目前分别针对客户满意度和物流配送车辆路径调度的研究成果很多,但大多是局限在二者范围内研究,前者仅有对客户满意度评价的一些研究,后者仅在算法方面作专门研究,总目标选取得大都简单,有很多目标项没有考虑到,没有针对性地给出配送调度方案。本文以服装业的配送问题作为研究对象,在日益激烈的市场竞争中,服装企业的成败不仅取决于其成本,还取决于其服务水平。
1 客户满意度
根据服装行业的特点,客户满意度的高低是个模糊概念,所以使用模糊度对评价指标进行描述有利于模型的研究。这里定义:物流配送客户满意度用介于0与1的数值进行表示,0表示客户对配送服务完全不满意,1表示客户对配送服务完全满意。
1.1 送货准时性对客户满意度的模糊描述
送货准时性反映了客户对货物到达时间的要求。在物流配送过程中,客户通常限定交货时间,货物必须在某一时间段内送达、卸货,如果过早或过迟,都会使客户满意度下降,从而影响客户满意度。时间段 [Tei,Tli],表示客户所能接受的服务时间段;时间段 [TEi,TLi]表示客户最满意的服务时间段。配送时间准时与否对客户满意度的影响可以通过图1表示出来。
1.2 构建客户满意度模糊函数
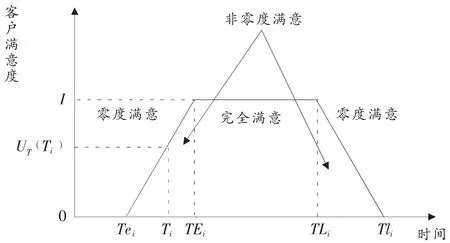
图1 客户满意度示意图
2 模型描述与设计
模型的假设条件: (1)单配送中心; (2)各配送点只被一辆车服务,而一辆车能为多配送点服务; (3)配送中心的车都是同一型号,即具有同样的最大配送量; (4)配送中心的产品能满足所有客户的需求。
设i=0表示配送中心,i=1,2…n表示第n个客户,hij表示客户i与客户j之间的距离,Ti表示配送到达客户i处的时间,si表示配送在客户i处的服务时间,tij表示从客户i行驶到客户j所需要的时间,Q为每辆车配送的最大配送量,F为每辆车配送的固定成本,di为客户i的需求量。
xijk=1表示第k辆车配送时,配送完点i后配送点j,否则xijk=0
rk=1表示第k辆车进行了配送,否则rk=0

约束条件:
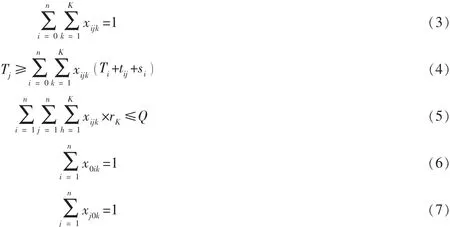
式中, i、j=1,2,…,n,k=1,2,…,K。
(1)表示成本最小化的目标; (2)表示客户满意度最大化的目标; (3)每个配送点只被一辆车服务的约束; (4)表示到达客户j的时间要晚于到达客户i的时间、为客户i服务的时间及客户i到客户j间的行驶时间之和; (5)车辆不允许超载; (6)、 (7)表示各个车辆从配送中心出发,服务客户后回到配送中心。
3 算法设计
本文先以配送成本最小为第一个目标函数,求解配送路线的客户组合,再以客户满意度最大为次目标,求解配送组合的客户配送顺序以及每次配送从配送中心出发的时间。用遗传算法求解的步骤:
(1)染色体编码。本文采用自然编码,即序数编码。车辆调度的一条可行线路可以编成长度为n+k的染色体, (0,i11,i12,…,i1s,…,0,i21,…,i2t,0,iml,…,imw),其中ikj表示第ikj个配送点。可以理解为车辆从配送中心出发,经过配送点i11,i12,...,i1s后,回到配送中心,形成子路径l;而第二辆车也是从配送中心出发,经过i21,...,i2t后,返回配送中心0,从而形成子路径2;如此反复,直到所有的客户都被访问到。这样,使染色体具有子路径内部有序,而各个子路径之间无序的特性。
(2)适应度函数。在车辆优化调度问题中,目标函数值越小越好 (即在满足载重量和时间约束的基础上,行车线路的总运距越小越好),而在遗传算法中,个体适应度越大,表示个体的性能越好,一般适应度函数要求非负,所以将目标函数通过变换fi=bz′zi转化为适应度函数。其中fi为染色体i的适应度;b为一常数;z′为初始群体中最好染色体的运输成本;zi为染色体i对应的运输成本。
(3)产生初始种群。由于基于某一特定的初始化策略会降低种群的多样性,一般采用随机生成的方法产生初始种群。初始种群是随机产生一个门店的全排列,并将第一位和最后一位置为0,表示从配送中心出发并最终回到配送中心, 如 (0,i1,i2,…i1,0 )。
(4)遗传算子。遗传算子主要包括交叉算子和变异算子。交叉算子是把两个父代个体的部分结构加以替换重组,而生成新个体,在遗传算法中起核心作用。交叉算子的设计一般与所求解的具体问题有关,而且要和编码方式相协调,就本文而言,对于染色体 (0,i11,i12,…,i1s,…,0,i2l,…,i2t,0,iml,…,imw),可以采用遗传算法标准的一点交叉(one-point crossover)、两点交叉 (two-point crossover)等。变异算子是对染色体的某些基因座上的基因值做变动,作用是维持群体的多样性。与二进制编码的变异操作不同,这里的变异是对个体某个基因的值随机产生。
用遗传算法对第一目标进行求解后,用客户满意度隶属函数UT(Ti)进行优化取得优化值。
4 算例分析
已知某个服装生产企业,设有1个自建配送中心 (0为配送中心),从配送中心出发,向4个不同门店配送服装产品。单位配送距离cij为1,配次的最大配送量Q为10m3,每辆车配送的固定成本F为100元,在每个客户的服务时间为0.5小时,该配送中心拥有足够被调度的车辆,设为K。其他相关数据如表1~4所示:
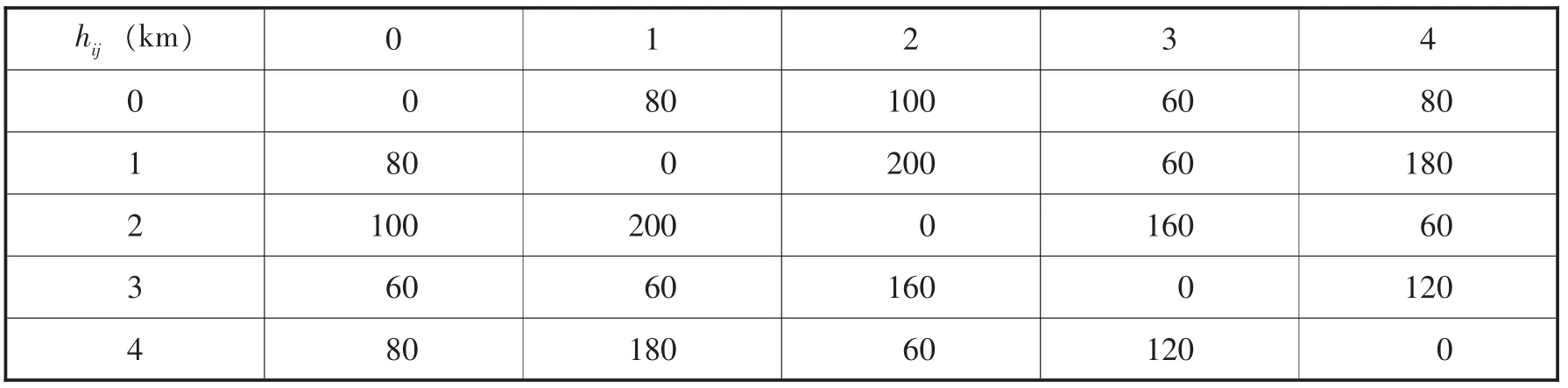
表1 配送中心、配送点间的距离
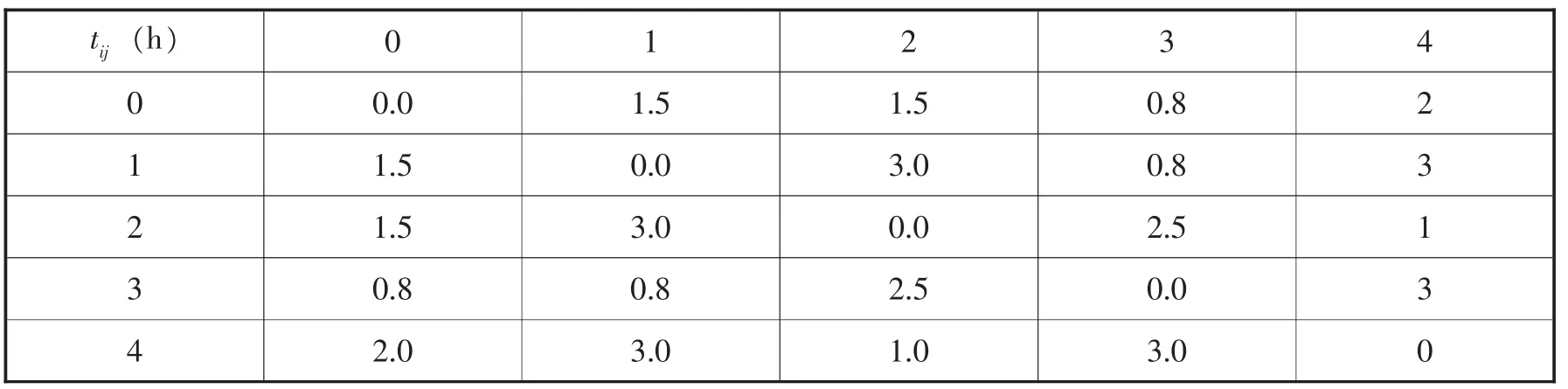
表2 配送中心、配送点间的行驶时间

表3 各需求点的需求特征
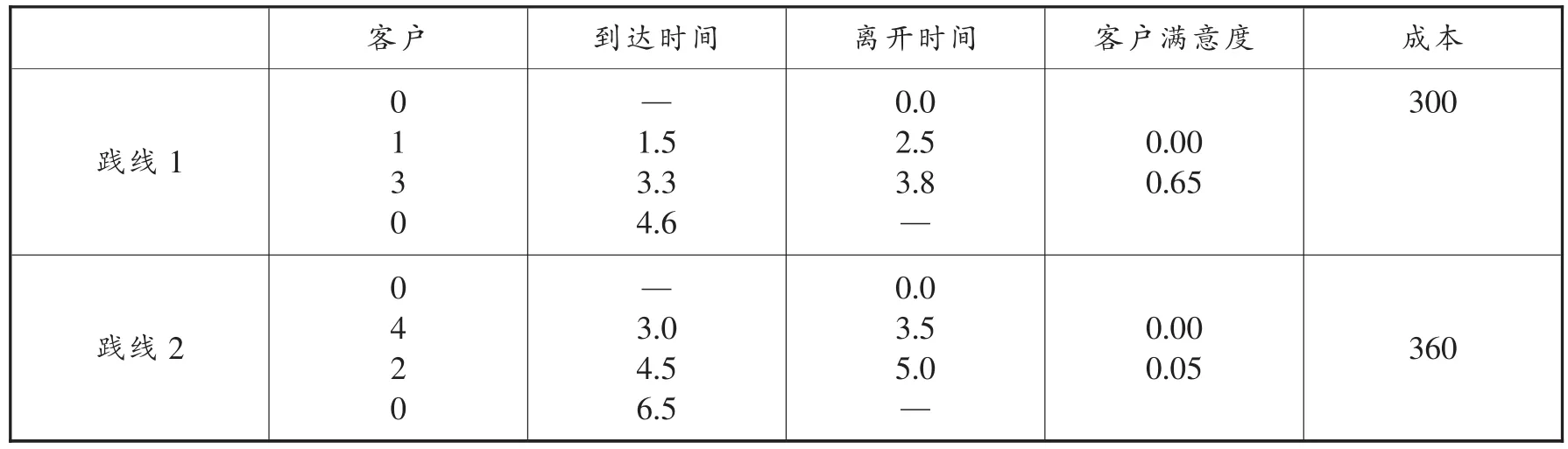
表4 以最小成本为目标用遗传算法进行求得的最佳配送组合
以客户满意度最大对上面结果在车辆的出行时间进行优化安排得到以下结果:
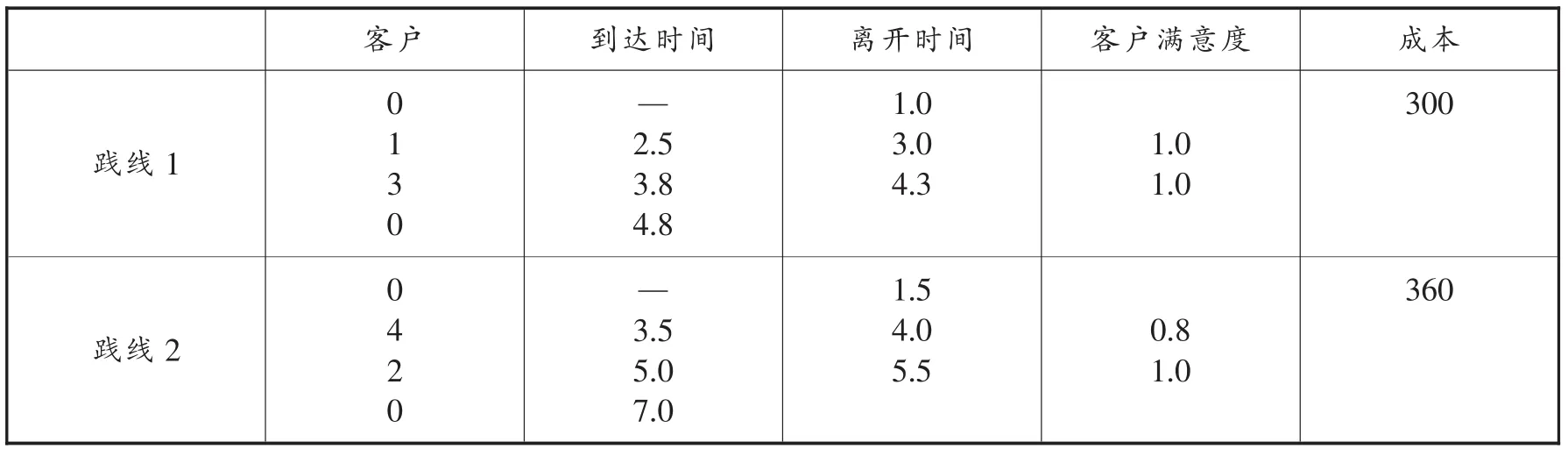
表5 优化后的结果
从表5可以看出,车辆线路一推迟一小时出发,线路2推迟1.5小时出发,可以提高客户满意度。
5 结 论
将车辆调度的成本最小化的目标与客户满意度进行结合,同时考虑客户的满意程度和配送成本,建立多目标配送模型,在节约配送成本的前提下,如何决策配送时间,尽可能在客户的期望时间段内提供配送服务,以期最大程度地提高客户满意程度,体现优质的配送服务水平,是企业提高配送质量的重要环节。
[1] 李军,郭耀煌.物流配送车辆优化调度理论与方法[M].北京:中国物资出版社,2001.
[2] 马昌荣.基于客户满意度的物流配送车辆优化探讨[D].上海:同济大学,2008.
[3] 王志远.基于遗传算法的服装连锁业车辆调度问题研究[J].新西部,2008(8):35-37.
[4] 林祖伟,方建斌,宋执环.基于Multi-agent的服饰企业分销与物流配送管理系统[J].纺织学报,2007,28(4):121-124.
[5]Gillett.B,Miller.L.A heuristic algorithm for the vehicle dispatch Problem[J].Operation Researeh,1974,22(6):340-349.

