金属蜂窝夹芯板辐射导热耦合问题

景 丽，王广飞，唐绍锋，梁 军

(哈尔滨工业大学复合材料与结构研究所，哈尔滨 150001，jingli315@163.com)

金属蜂窝夹芯板辐射导热耦合问题

景 丽，王广飞，唐绍锋，梁 军

(哈尔滨工业大学复合材料与结构研究所，哈尔滨 150001，jingli315@163.com)

针对金属蜂窝夹芯板，研究了其在气动加热条件下的非稳态传热行为.基于高温传热学原理，通过传热机制分析，建立了蜂窝夹芯板的导热－辐射一维瞬态耦合传热数学物理模型.在此基础上，采用控制容积法，结合蒙特卡罗法，发展形成了求解该类辐射导热耦合传热问题的数值方法，并给出了蜂窝夹芯板当量热导率和典型边界条件下金属蜂窝夹芯板瞬态温度场、非加热面热响应的计算方法，进行了典型算例计算和实验验证.结果表明，所建立的数值计算模型在预报蜂窝结构热响应方面是有效的，而且较之Swann-Pittman半经验关系式，提高了计算精度.

蜂窝夹芯板;辐射导热耦合;当量热导率;数值预报

针对蜂窝夹芯板结构的传热研究大多是从无限大蜂窝夹芯板中选取周期分布的胞元，假定温度沿板厚度方向线性分布［1］，或者二次函数分布［2］，或者某种多项式分布［3］，通过有限元计算结构的有效热导率.近年来，在蜂窝夹芯结构热分析理论和计算分析方面YI Long等［4］选取高阶单元、采用高斯积分精确对单元表面变辐射热流进行了研究.N.D.Kaushika等［5］推导了一种基于蜂窝芯层为灰体假设的物理模型，计算了蜂窝结构的辐射换热量.Swann-Pittman半经验关系式［6］已被做为一个标准模型用来计算蜂窝结构的热传导问题.

本文在进行蜂窝夹芯腔体内部传热机制分析的基础上建立了蜂窝板导热－辐射一维瞬态耦合传热数学物理模型.采用控制容积法，结合蒙特卡罗法［7］，发展形成了求解该类辐射导热耦合传热问题的数值方法.给出了蜂窝夹芯板当量热导率并揭示不同温度下影响当量热导率的主导因素，并给出了典型边界条件下金属蜂窝夹芯板瞬态温度场、非加热面热响应的计算方法.

1 瞬态导热－辐射耦合传热过程的理论模型

1.1 传热机制及当量热导率的计算

蜂窝板由上、下蒙皮及中间蜂窝芯层构成，蜂窝板外表面在气动热流加热下导致外表面温度升高，外表面蒙皮将对外辐射能量，通过外表面蒙皮将大部分的热量qR辐射回大气环境，其余热量qa以热传导的方式进入蜂窝板.当蜂窝尺寸在一定的范围内时，通过蜂窝胞体腔内空气对流传递的热量可以忽略［8］，因此，蜂窝内部的热量传递主要由传导和辐射的耦合作用完成.如图1所示，蜂窝板内存在3种热量传递机制:1)蜂窝腔表面间的辐射换热qr.2)固体壁面的热传导qsc.3)蜂窝腔内气体的导热qg.

图1 蜂窝板内传热机理模型

计算蜂窝芯层当量热导率，给出边界条件为

式中:Tw1，Tw2分别为上、下边界温度，H为蜂窝夹芯板厚度，x=0面为非加热面.

按上述边界条件求解蜂窝传热控制方程，可以获得稳态温度场，进而计算得到蜂窝下底面上的导热热流密度大小为

式中:keff为蜂窝的有效导热系数，根据蜂窝芯层固体和气体两相体积分数进行平均计算.文中普遍使用串联模型，即

式中:ε为气相所占有的体积分数，ks，kg分别为固相［9］和气相［10－11］导热系数.

下边界面上的总热流密度为导热热流密度与下边界面上接收到的辐射热流密度之和，即

式中:qrad为采用蒙特卡罗方法计算的下边界面上的辐射热流密度.

1.2 非稳态温度场的计算

蜂窝结构具有周期性，可以将其中一个蜂窝单元作为研究对象，如图2所示.以壁面的中间面作为绝热边界面.金属蜂窝结构尺寸都不大，计算的Ra数一般很小，可以忽略自然对流换热作用.沿蜂窝板厚度方向的一维非稳态传热控制方程为

式中:T为热力学温度，t为时间，ρ，c，k分别为蜂窝芯的有效密度、有效比热与有效导热系数.S为蜂窝腔体内表面间辐射换热源项，采用蒙特卡罗方法计算.其中，蜂窝芯的有效密度根据两相材料密度和体积分数进行平均为

式中:ρs为蜂窝芯金属密度，ρg为蜂窝内气体密度，As，Ag分别为蜂窝单元横截面内固相和气相所占有的面积.

图2 正六边形蜂窝单元

蜂窝芯的有效比热根据两相比热和体积分数进行平均，即

式中:cs，cg分别为固相和气相的比热.

蜂窝内某一控制体单元ΔVi的辐射换热源项为

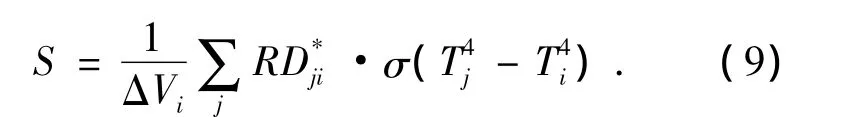
式中:σ为黑体辐射常数，RD*ji为归一化辐射传递系数，对控制体ΔVi上参与辐射换热的面元ΔAj有RD*ji= εj·ΔAj·RDji，其中，RDji为辐射传递系数，表示单位时间内蜂窝腔内面积单元ΔAj发射的热辐射能最终被单元ΔAi吸收的部分，Tj，Ti分别为面积单元ΔAj、ΔAi的温度.

在3类边界条件下求解蜂窝夹芯结构非稳态传热控制方程，得到温度场，实现蜂窝夹芯结构传热分析.为方便起见，初始条件均为

式中:Tw1，Tw2分别为上、下边界温度，H为蜂窝夹芯板厚度，x=0面为非加热面.

2)第2类边界条件.

由于蜂窝面板通常在热防护系统最外层，而且温度高，是对环境的辐射散热表面，因此，要考虑表面对环境的辐射散热;此外，蜂窝夹芯板两侧的蒙皮具有一定的质量，虽然非常薄，如果忽略它的质量可能会引入较大的误差，因此，将蜂窝夹芯结构考虑为一个具有一定质量，并且对环境辐射散热的边界，它的质量等于蜂窝夹芯板的蒙皮质量，则给定环境热流密度的第2类边界条件为

式中:qBD为外界环境对边界的热流密度，εBD为边界对外界环境的发射率，qradint为边界面向蜂窝腔内部的辐射热流密度，qcondint为边界面蜂窝腔内部的导热热流密度，ρ，cp，L分别为蒙皮的密度、比热、厚度，τ为非稳态过程的时间.

3)第三类边界条件.

由于蜂窝面板的非加热面是对外界流体的对流换热表面，基于第2类边界条件，考虑蜂窝夹芯板蒙皮质量和对流换热的第3类边界条件可以写为

式中:αBD为外界流体对边界的对流换热系数，Tf为外界流体温度.

1.3 辐射导热耦合换热控制方程的数值求解

蜂窝板内辐射导热耦合传热数值计算分为温度场迭代求解与辐射换热场的计算求解.

在温度场迭代求解过程中，将能量方程中的辐射换热处理为源项，使辐射－导热耦合传热能量方程具有导热微分方程的形式，从而将辐射－导热耦合传热计算分解为辐射换热源项计算、含源项的导热微分方程求解两个子过程，通过这两个子过程迭代，实现耦合传热计算.采用控制容积法［12］对计算域进行均匀离散，边界条件的处理采用补充边界节点离散代数方程［13］方法，由于辐射源项的非线性，在开发热分析计算模块过程中采用了欠松弛迭代［14］，以保证数值计算的稳定.

在辐射换热场的计算过程中，采用蒙特卡罗法将热辐射的传输过程分解为发射、反射、吸收、散射等一系列独立的子过程，并建立每个过程的概率模型.对每个单元(面元和体元)进行一定数目的能束抽样，跟踪、统计每束能束的归宿(被介质和界面吸收或从系统中逸出)，从而获得辐射传递因子.通过引入各离散单元之间的辐射传递系数，将辐射传递过程求解与温度场求解分离，从而大大降低辐射换热的求解复杂性，提高了辐射导热耦合换热数值计算的计算效率.

2 数值结果与验证

2.1 当量热导率的数值求解

蜂窝芯结构参数如表1所示，上、下面板与蜂窝芯材料均为 Haynes 214，气体压力 1.013×105Pa，计算中光子抽样个数为105，温度场迭代误差为10－5K.

表1 蜂窝几何参数

研究辐射换热对蜂窝夹芯结构当量热导率的影响，当蜂窝腔发射率分别取值为0.86、0.50和0. 10，上、下边界温度相差10 K时当量热导率随温度变化的计算结果对比如图3所示.对比显示随着温度的升高，辐射换热的影响会逐步增强，如不考虑它的影响，就会给计算结果带来很大误差.

图3 不同发射率下蜂窝当量热导率

2.2 传热分析及实验验证

为了进行实验验证分析，设计制造了高真空平板石墨加热炉，可以实现对大尺寸(450 mm×450 mm×5 mm～80 mm)试件乃至热防护系统整体样件防、隔热性能的测试，最高加热温度可达1 600℃、可控压力范围6.67×10－3～1.013 25×105Pa.炉体内结构示意图如图4所示.

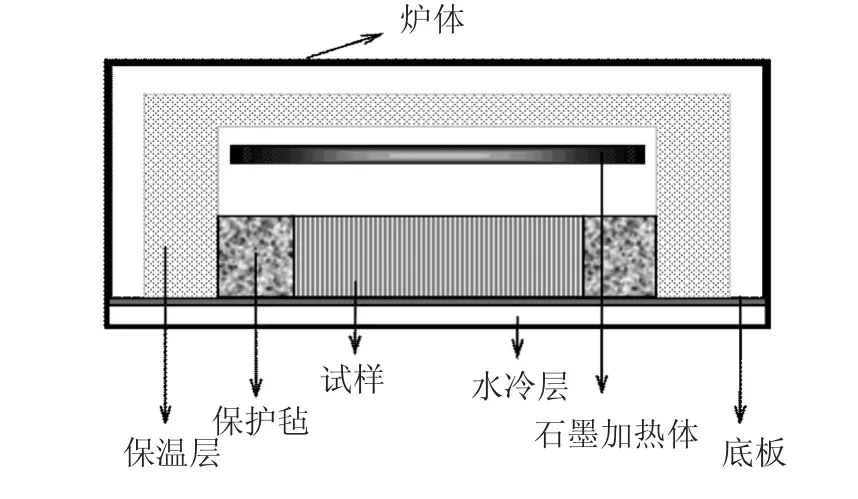
图4 加热炉真空室示意图

用于实验测试的试样为INCONEL 617蜂窝夹芯板，尺寸为200 mm×200 mm×5 mm，蒙皮厚度为0.12 mm，单元胞壁厚度为0.076 mm，蜂窝直径5.6 mm，输出控制热流为40 kW/m2.为了避免边界的影响，将试样中心125 mm×12 5 mm的区域作为数据采集区，在试样和水冷板之间铺设了9只K型热电偶及3只热流传感器，如图5所示.在试样的上表面放置了3只K型热电偶，位置与图5中热流传感器的位置相同.温度和热流数据的采集采用多路温度测量仪，利用计算机窗口实时监控和记录实验数据，实验在氮气环境下完成.

图5 实验装置简图

1)边界条件.由于加热表面直接与热源接触，边界条件为施加的热流密度即第2类边界条件.而对于非加热表面，为更接近实际条件，必须考虑蜂窝夹芯板蒙皮质量和与对流换热的影响，因此采用了第3类边界条件，根据水平放置平板自然对流换热关联式［15］，与下冷水板的对流换热系数取4.6 W/(m2·K).

2)初始条件.室内空气温度取293 K，初始温度为293 K.

蜂窝板外表面发射率取0. 86，内表面发射率按照被氧化了的铝表面发射率取值为0.3［16］.蒙特卡罗模拟过程中每个表面单元发射能束数目取为105，能量方程迭代计算误差取为10－5J.

蜂窝夹芯板热分析计算模块给出的蜂窝板上、下蒙皮表面温度响应与实验结果对比如图6所示，对比显示计算结果与实验结果吻合很好.

图6 计算结果与实验结果比较

图7给出了数值计算所得50 s时沿厚度x方向的温度分布，其中，x=0 mm为非加热面，x=5 mm为加热面.从图7可以看出，温度分布呈现很规则的线性规律，其趋势同文献［17］中吻合.

图7 在50 s时沿厚度方向的温度分布

对于厚度为H的试样，一维热传导达到稳态后，若热边、冷边温度及通过试样的热流分别为:Theat、Tcool、q，则试样的当量热导率为

图8给出了蜂窝板当量热导率计算模块给出的不同温度下采用相同热边界条件时，当量热导率计算结果、实验结果与Swann-Pittman半经验公式计算结果的比较.

图8 蜂窝夹芯板的当量热导率的比较

结果表明，实验结果预报结果在温度较低时存在一定误差，相对误差最大为24%，本文认为引起误差的来源主要包括:热流值、温度值以及厚度值的测量误差.超过573 K后预报值与实验值相对误差小于6%，两者吻合较好.较之根据数值结果拟合的Swann-Pittman半经验公式，辐射导热的耦合计算采用热网络法和蒙特卡罗法，在计算精度、应用范围上都有提高.

3 结论

1)通过传热机制分析，建立了蜂窝夹芯板的导热－辐射瞬态耦合传热数学物理模型及数值求解方法，经过典型算例计算和实验验证表明该方法是正确的，适合金属热防护系统蜂窝夹芯结构的传热分析.

2)根据计算结果分析，随着温度的升高，夹芯结构内部辐射换热的影响会逐步增强，与实验结果吻合较好;当温度超过573 K后，本方法预报值比Swann-Pittman半经验公式计算结果更接近实验值，相对误差小于6%.

3)本文建立的辐射导热耦合计算方法在揭示蜂窝夹芯板传热机制、计算精度和应用范围上都有提高.

［1］TENEK L，ARGYRIS J，OEBERG F.A multilayer composite triangular element for steady-state conduction/convection/radiation heat transfer in complex shells［J］.Computer Methods in Applied Mechanics and Engineering， 1994，120(3/4):271－301.

［2］王勖成，唐永进.一般壳体温度场的有限元分析［J］.清华大学学报(自然科学版)， 1989，29(5):103－111.

［3］SURANA K S，ORTH N J.Completely hierarchical P－version anisymmetric shell element for nonlinear heat conduction in laminated composites［J］.Computers ＆Structures， 1992，46(5):777－789.

［4］YI Long，PENG Yun，SUN Qin.Research of the higher-order finite element arithme-tic for radiation exchange［J］.Chinese Journal of Aeronautics， 2006，9(3):197－202.

［5］KAUSHIKA N D，ARULANANTHAM M.Radiative heat transfer across transparent honey-comb insulation materials［J］.Heat Mass Transfer， 1995，22(5):751 －760.

［6］DARYABEIGI K.Heat transfer in adhesively bonded honeycomb core panels［J］.Journal of Thermophysics and Heat Transfer， 2002，16(2):217－221.

［7］HOWELL J R.Monte Carlo method in radiative heat transfer［J］.Journal of Heat Transfer， 1998，120(3)，547－560.

［8］KAUSHIKA N D，PADMAPRIYA R，SINGH T P.Convection theory of honeycomb and slat-devices for solar energy applications［J］.Energy Res Technol， 1992，35(2):126－146.

［9］KAMRAN D.Effective Thermal Conductivity of High Temperature Insulations for Reusable Launch Vehicles［R］.Washington，DC:NASA Technical memorandum，1999:208972.

［10］KAMRAN D.Thermal Analysis and Design of Multilayer Insulation for Re-entry Aerodynamic Heating［R］.Easton，PA:AIAA，2001:2001－2834.

［11］POTEET C，KHAJEEL H A，HSU S Y.Preliminary Thermal-Mechanical Sizing of Metallic TPS［R］.Easton，PA:AIAA，2002:2002－0505.

［12］鲁怀敏.用控制容积法求解连铸方坯温度场［J］.沙洲职业工学院学报， 2004，7(1):12－21.

［13］杨世铭.传热学［M］.北京:高等教育出版社，2006:167－169.

［14］葛德彪.平面介质波导折射率剖面重建的欠松弛迭代方法［J］.光子学， 1996，25(5):439－445.

［15］杨世铭.传热学［M］.北京;高等教育出版社，2006:212.

［16］杨世铭.传热学［M］.北京:高等教育出版社，2006:369.

［17］陈勇，高德平.金属蜂窝平板加热过程的数值模拟及试验研究［J］.理化检验(2)物理分册， 2003，39(5):234－236.

Radiation and conduction coupling problems of honeycomb sandwich panel

JING Li，WANG Guang-fei，TANG Shao-feng，LIANG Jun
(Centre for Composite Materials and Structures，Harbin Institute of Technology，Harbin 150001，China，jingli315@163.com)

In this paper，the non-steady-state heats transfer behavior of metal honeycomb sandwich panel under aerodynamic heating was studied.Based on high temperature heat transfer theory and mechanism analysis，one-dimensional transient heat transfer mathematical physics model of honeycomb sandwich panel taking the combination of heat conduction and radiation into account was given.The control volume method and Monte Carlo method were adopted and then a numerical computation method was developed to calculate the coupling problem of heat conduction and radiation.Computation methods for effective thermal conductivities of honeycomb sandwich panel，the transient temperature field and heat response of non-heated surface under typical boundary conditions were given as well.An experiment was designed to validate this computation method.The result shows that the numerical computation model given in this paper is valid to predict the thermal performance of honeycomb sandwich structures and the values calculated are more precise than those calculated by Swann-Pittman semi-empirical relationship.

honeycomb sandwich panel;combination of heat conduction and radiation;effective thermal conductivities;numerical prediction

V435

A

0367－6234(2010)05－0827－05

2009－06－22.

国家自然科学基金资助项目( 10772060，90916027);

黑龙江省杰出青年基金资助项目(JC2006-13).

景 丽(1984—)，女，硕士研究生;

梁 军(1969—)，男，教授，博士生导师.

(编辑 张 红)