输入受限的航天器姿态调节小波滑模反步控制

胡庆雷，肖 冰，马广富

(哈尔滨工业大学控制科学与工程系，哈尔滨 150001，huqinglei@hit.edu.cn)

输入受限的航天器姿态调节小波滑模反步控制

胡庆雷，肖 冰，马广富

(哈尔滨工业大学控制科学与工程系，哈尔滨 150001，huqinglei@hit.edu.cn)

对刚体卫星在轨机动时存在未知惯量特性、外部干扰及控制输入受限的控制问题，提出了一种将滑模反步姿态控制与小波相结合的鲁棒控制方法，这种方法在继承传统滑模反步控制的优点的同时，利用小波函数的逼近能力来补偿执行机构饱和非线性;对设计者而言，饱和非线性的结构特性无需了解，并基于Lyapunov方法从理论上证明了滑动模态的存在性及系统的全局稳定性.最后，将该方法应用于航天器的姿态调节控制，仿真结果表明此控制器能有效地处理航天器姿态调节过程中控制输入饱和受限的约束，在完成姿态调节控制的同时，具有良好的过渡过程品质.

姿态调节;反步法;滑模控制;小波神经网络

现代航天器是一个变参数、强耦合的不确定多变量的以及存在外在各种干扰的非线性系统;而且由于受到外部干扰力矩的作用，导致星上的执行机构是输出饱和的，这种控制输入饱和特性的存在降低了系统的性能，甚至使系统表现出不稳定的特性;因此研究带有执行机构输出饱和的航天器的高性能姿态调节控制成为发展现代航天器的核心技术之一.

滑模变结构控制对系统匹配参数不确定性和干扰具备很好的鲁棒性，且其算法实现起来相对简单，在航天器的控制上得到了广泛的应用［1－5］;然而在实际系统中，滑模变结构控制器本身不能克服系统中非匹配不确定性，而仅考虑匹配不确定性的变结构控制是不够的;Backstepping(反步)设计方法作为另一种鲁棒控制方法，可以有效地处理非匹配参数不确定性的非线性系统［6－7］，利用小波神经网络对非线性函数的逼近能力，并与其相结合，从理论上来说，可以处理更广泛的系统，目前在这方面无论是理论上还是应用上都有很丰富的研究结果［8－9］.

为此，针对带有输入控制饱和的航天器姿态调节问题，本文提出了一种小波滑模反步姿态控制方法.在航天器非线性动力学模型的基础上，应用自适应滑模控制技术来处理不确定性和外干扰上界未知的问题;并利用小波网络函数逼近能力来补偿执行机构饱和非线性，同时使用Lyapunov法分析了滑动模态的存在性及系统的全局渐近稳定性.最后，将该控制方法应用于航天器的姿态调节控制，仿真结果表明该方法在控制受限条件下，能完成姿态调节控制，且具有良好的过渡过程品质.

1 航天器数学模型

本文采用姿态四元数法来描述航天器姿态.其姿态动力学方程以及运动学方程为

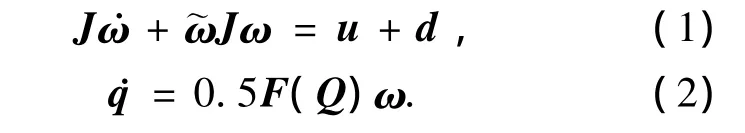
式中:u为航天器的控制力矩;d为航天器受到的环境干扰力矩;J为航天器的转动惯量矩阵;ω=(ω1，ω2，ω3)T为星体角速度;Q=(q0，qT)T表示本体坐标系和惯性坐标系间的姿态四元数，且满足

式(3)中E3为3阶单位阵;定义为

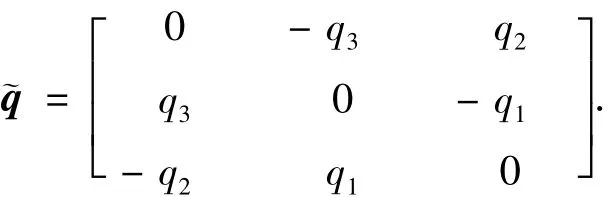
对于系统(1)～(2)作如下假设.

假设1 转动惯量矩阵J是未知的，但J是正定对称的，且

假设3 干扰力矩d=(d1，d2，d3)T有界，其中 |di|≤ Di，i= 1， 2， 3，并且 Di未知.

本文的控制目标是针对式(1)～(4)描述的航天器姿态调节系统，在假设1～3的前提下，设计控制律u确保闭环系统渐近稳定，也即当t→∞时有q→0以及ω→0.

2 姿态调节控制器设计

首先采用Backstepping方法构造下面的变量变换:

β1是一虚拟控制输入，其值将在后面给出.

1)选取Laypunov函数

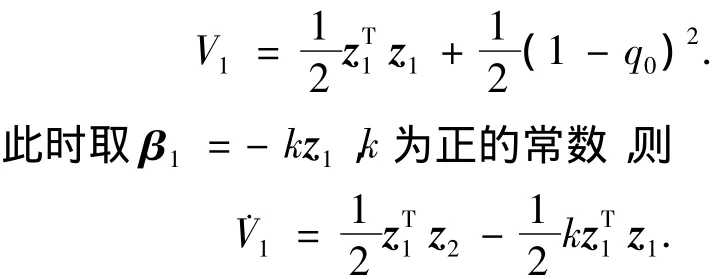
由此式可知当z2=0时˙V1＜ 0，从而z1将渐近收敛至0.

2)式(6)对时间求导，并且两边同乘以J得

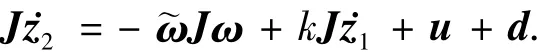
由于J是未知的，通过如下的变换把J中的元素分离出来，得

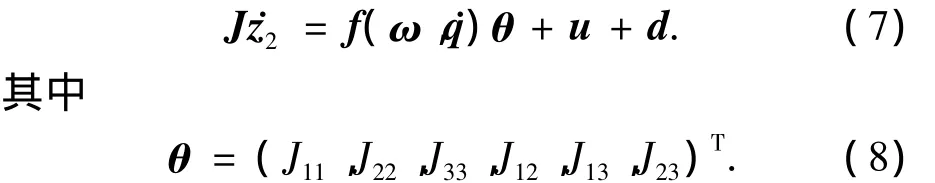
此时，选取滑模面

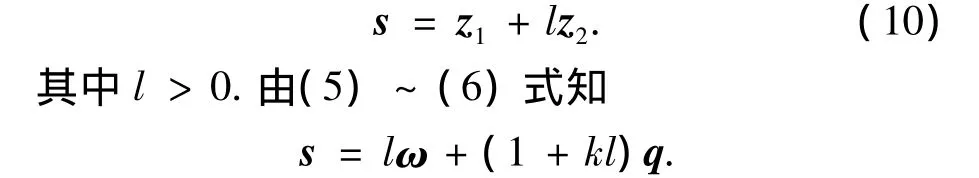
由文献［5］知在这样的滑模面上滑动时，当t→∞ 时有z1→0和z2→ 0，即q→0和ω→0.

由式(7)和(10)可得出

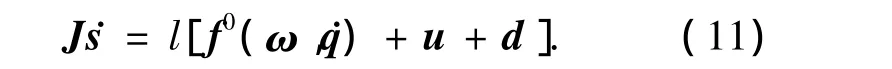
其中只要把(9)式中的k变成k+l－1就为f0(ω，˙q).

由假设2知，式(11)中的控制力矩u的大小受限，这里采用下面的反正切函数来逼近ui［6］.

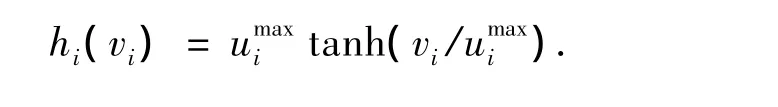
将上式代入(11)式有

因g中的各元素都是未知的，而小波神经网络的逼近精度要比一般的神经网络的逼近精度高［10］，本文将使用小波神经网络来逼近g中的每一个元素gi.

2.1 小波神经网络逼近

文献［9］表明可以用m个节点的小波神经网络来逼近函数g，形式如下:

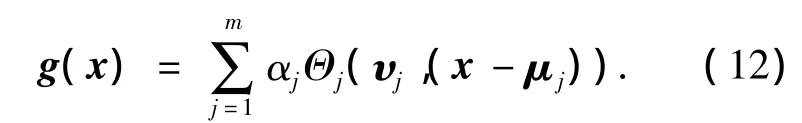
式中:x=(x1，x2，…，xn)T是输入向量，Θj(υj，(x － μj))是小波基函数，υj=(υ1j，υ2j，…，υmj)T和μj=(μ1j，μ2j，…，μmj)T分别是扩张和平移参数，αj∈R是输出层权重，其结构如图1所示.

图1 小波神经网络结构

本文采用墨西哥草帽函数作为小波基函数，即

结合上两式便可将(12)写成向量形式

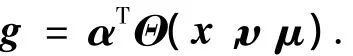
由全局逼近定理知存在最佳的小波网络g*满足

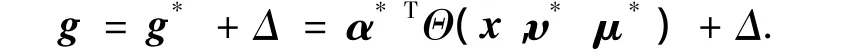
其中 α*，υ*，μ*分别是 α，υ，μ 的最佳逼近向量，Δ是逼近误差，且满足|Δ*|.然而g*的参量很难求出，因此不妨定义g*的估计函数为

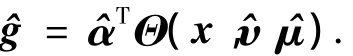
2.2 小波滑模反步控制器的设计

利用上述小波神经网络去逼近gi得

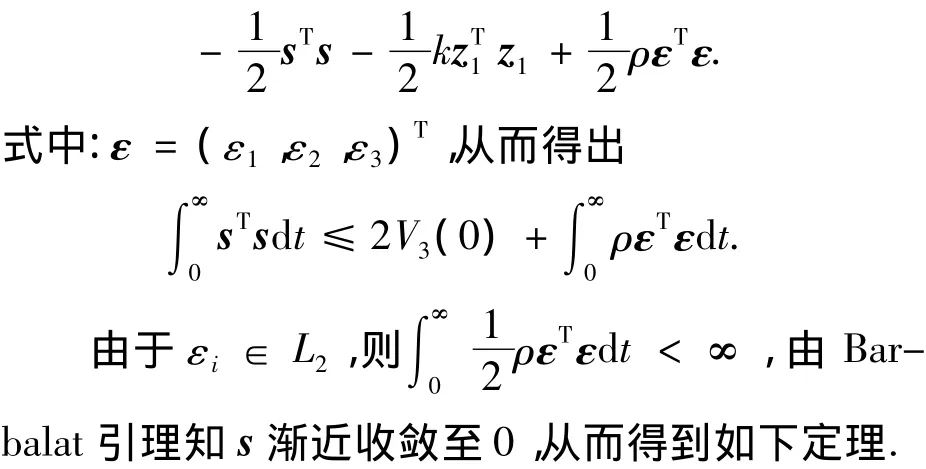
定理1 考虑系统(1)～(2)且满足输入饱和受限的约束，如果假设1～4成立，选择控制器(15)且自适应控制律(16)～(20)的参数满足其设计要求，则闭环系统是全局渐近稳定，即当t→∞ 时，有q→ 0，ω→0.

证明 定理1的证明可由上述推导得到，在此略去.

3 仿真结果和比较

为了验证上述设计方法的有效性，采用文献［7］中所给出的航天器的物理参数和外部干扰力矩.航天器姿态初始值设定为

采用文中的小波滑模反步控制器(15)，控制参数取值为k= 1，l= 10，γ1= 5，γ2= 5，γ3= 5，γ4= 5，γ5=5和ρ=0.07.小波神经网络的节点m= 5，初始化小波神经网络中的参量αi(0)=υi(0)=μi(0)=0.仿真结果如图2～4所示，在完成姿态调节的同时，其过渡过程比较平稳，且控制力矩的输出满足其幅值的要求，如图4所示.

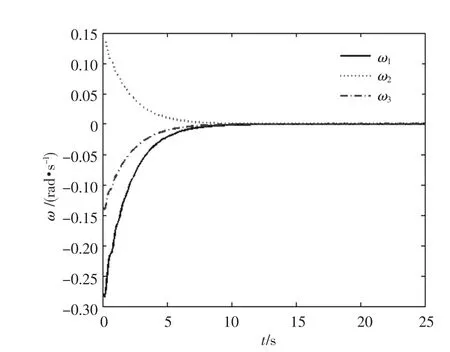
图2 角速度的变化情况

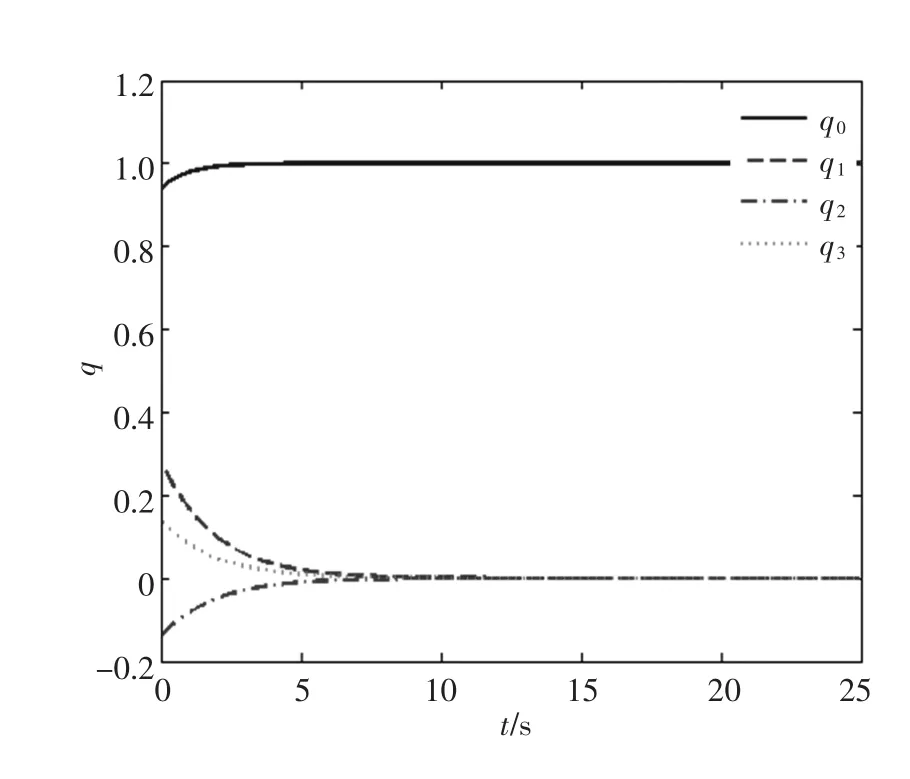
图3 四元数的变化情况

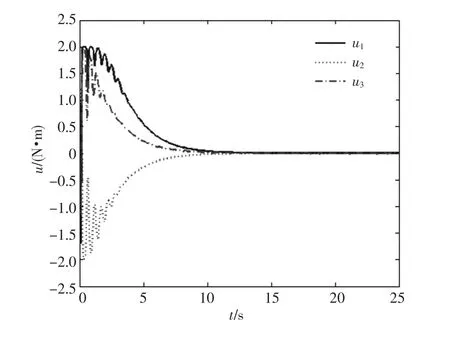
图4 控制输入u的变化情况

为了便于比较，本文也采用传统的PD控制方法来实现上述含控制输入饱和的姿态调节控制，PD控制器设计为

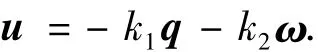
控制参数k1=10和k2=10.仿真结果如图5～7所示，存在较大的超调和震荡，并且系统的响应速度较慢，大约80 s完成姿态调节.

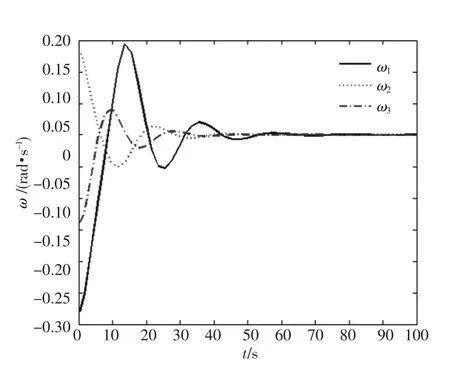
图5 角速度的变化情况

图6 四元数的变化情况

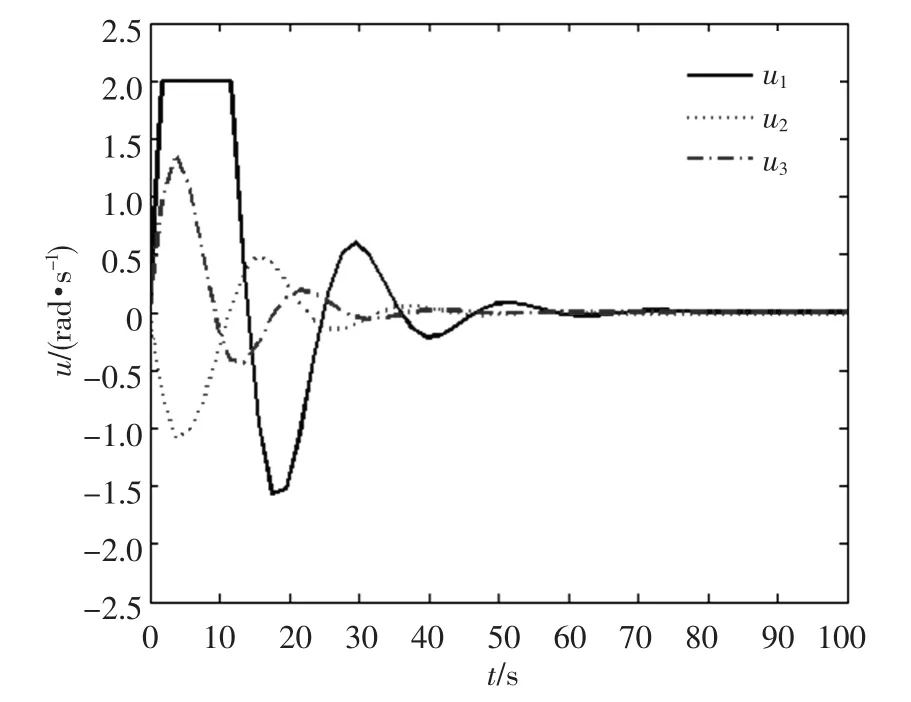
图7 控制输入u的变化情况

4 结论

针对刚体卫星本身存在着模型不确定性因素、受到外部扰动的作用以及执行机构存在饱和的问题，本文提出了小波滑模反步控制律设计方法.小波网络的引入使得控制器具有很强的自适应和自学习能力，降低饱和非线性对系统的影响和改善了系统的稳态性能，以保持机动过程的平稳性，另外，自适应控制技术的引入，同时也克服确定不确定性和外干扰界函数上限的困难.将本文提出的控制方法应用于航天器的姿态调节控制，结果表明该方法保证在完成了姿态调节控制的同时，都具有良好的过渡过程品质，有着广泛的应用前景.

［1］HU Q L，MA G F.Control of three－axis stabilized flexible spacecrafts using variable structure strategies subject to input nonlinearities［J］.SAGE Journal of Vibration and Control， 2006，12(6):659 －681.

［2］HU Q L，MA G F.Variable structure control and active vibration suppression of flexible spacecraft during attitude maneuver［J］.Aerospace Science and Technology， 2005，.9(4):307 －317.

［3］BOŠKOVI C′J D，LI S M，MEHRA R K.Robust adaptive variable structure control of spacecraft under control input saturation［J］.Journal of Guidance，Control and Dynamics， 2001，24(1):14－22.

［4］WALLSGROVE R J.Globally stabilizing saturated attitude control in the presence of bounded unknown disturbance［J］.Jouranl of Guidance，Control and Dynamics， 2005，28(5):957－963.

［5］VADALI S R.Variable structure control of spacecraft large attitude maneuvers［J］.Journal of Guidance，Control and Dynamics， 1986，9(3):235 －239.

［6］ZHOU J，ER M，ZHOU Y.Adaptive neural network control of uncertain nonlinear systems in the presence of input saturation［C］//9th International Conference on Control，Automation，Robotics and Vision.Singapore:［s.n.］，2006.

［7］宋斌，李传江，马广富.航天器姿态机动的鲁棒自适应控制器设计［J］.宇航学报， 2008，29(1):121－125.

［8］GAO W Z，SELMIC R R.Neural network control of a class of nonlinear systems with actuator saturation［J］.IEEE Transactions on Neural Networks， 2006，17(1):147－156.

［9］CHUN F H.Wavelet adaptive Backstepping control for a class of nonlinear systems［J］.IEEE Transactions on neural networks， 2006，17(5):1175－1183.

［10］DELYON B，JUDITSKY A，BENVENISTE A.Accuracy analysis for wavelet approximations［J］.IEEE Transactions on Neural Networks， 1995，6:332 －348.

Wavelet based backstepping sliding mode control for spacecraft attitude regulation under control input constraint

HU Qing－lei，XIAO Bing，MA Guang－fu

(Dept.of Control Science and Engineering，Harbin Institute of Technology，Harbin 150001，China，huqinglei@hit.edu.cn)

In this paper，a wavelet based backstepping sliding mode controller for rotational maneuver is proposed for an orbiting three－axis stabilized spacecraft，taking the actuator saturation into account.Wavelet networks，which have superior learning capability in comparison to conventional neural network，are used for approximation of unknown system dynamics.This proposed controller comprises of a wavelet based saturation compensator and a robust backstepping sliding mode controller，and the latter one is designed to achieve the desired performance by attenuating the effect of approximation error caused by wavelet identifier.Lyapunov stability analysis shows that the resulting closed－loop system is globally asymptotically stable.To study the effectiveness of the corresponding control scheme，traditional methods are also developed for the control system.Both analytical and numerical results are presented to show the theoretical and practical merit of this approach.

attitude regulation;backstepping;sliding mode control;wavelet neural network

V448.2

A

0367－6234(2010)05－0678－05

2009－04－11.

国家自然科学基金(60774062);高等学校博士学科点专项科研基金(20070213061);中央高校基本科研业务费专项资金(HIT.NSRIF.2009003);黑龙江省留学回国人员科学基金(LC08C01)，哈尔滨市留学回国基金(2010RFLXG001).

胡庆雷(1979—)，男，副教授，博士生导师;

马广富(1963—)，男，教授，博士生导师.

(编辑 张 宏)